
* A Distributed Proofreaders Canada eBook *
This eBook is made available at no cost and with very few restrictions. These restrictions apply only if (1) you make a change in the eBook (other than alteration for different display devices), or (2) you are making commercial use of the eBook. If either of these conditions applies, please check with an FP administrator before proceeding.
This work is in the Canadian public domain, but may be under copyright in some countries. If you live outside Canada, check your country's copyright laws. If the book is under copyright in your country, do not download or redistribute this file.
Title: Astronomical Thought in Renaissance England
Date of first publication: 1937
Author: Francis R. Johnson
Date first posted: Sep. 11, 2013
Date last updated: Sep. 11, 2013
Faded Page eBook #20130910
This eBook was produced by: Stephen Hutcheson & the online Distributed Proofreaders Canada team at http://www.pgdpcanada.net

HUNTINGTON LIBRARY PUBLICATIONS
ASTRONOMICAL THOUGHT IN RENAISSANCE ENGLAND
A Study of the English Scientific Writings from 1500 to 1645
A Study of the English Scientific Writings
from 1500 to 1645
By
FRANCIS R. JOHNSON
1968
OCTAGON BOOKS, INC.
New York
Copyright, 1937, The Johns Hopkins Press
Reprinted 1968
by special arrangement with Ruth M. Johnson
OCTAGON BOOKS, INC.
175 Fifth Avenue
New York, N. Y. 10010
Library of Congress Catalog Card Number: 68-27334
Printed in U.S.A. by
NOBLE OFFSET PRINTERS, INC.
NEW YORK 3, N. Y.
To R. M. J.
The influence of the scientific movement on literature and ideas in the English Renaissance has received the increasing attention of scholars in recent years, yet thus far little has been known at first hand of the scientific writings of that age. Most studies have confined themselves chiefly to the literary and philosophical works when dealing with the century and a half preceding the first gatherings of the group of scientists who later founded the Royal Society. The purpose of this volume, on the other hand, is to survey the English writings on science from about 1500 to the mid-seventeenth century, in order to chart the course of astronomical thought in scientific circles during that significant period of transition from the old cosmology to the new. It will therefore present the results of a first exploration in territory hitherto almost wholly uncharted.
The original design for this study, first begun some six years ago, grew out of the conviction that no trustworthy appraisal of the influence of the scientific movement upon contemporary thought could be made without first understanding thoroughly the spirit and the ideas prevailing among the scientists themselves. Many currents of nonscientific speculation, both metaphysical and religious, were of course involved in the shifting from the old to the new theories of the universe. Yet I believe that students of the Renaissance will grant that the soundest point of departure for an analysis of the progress of the new astronomy should be found in the popular works of those English scientists whom their contemporaries regarded as their most eminent astronomers.
Unfortunately, it is precisely these scientific works which have been least known and most inaccessible to scholars. Consequently, a thorough survey of the once familiar but now forgotten treatises on astronomy and related sciences should make available the material for a more complete understanding of the influence of the new cosmology upon contemporary thought, [viii] and for the clearing up of many prevailing misconceptions concerning Renaissance astronomical ideas.
The scope of this book has therefore been intentionally restricted. Its attention will be centered upon the changes in astronomical beliefs as they are set forth by the scientific writers of the time, and upon the general attitude toward the aims and methods of science which these writers reveal. Because of this somewhat arbitrary limitation, dictated by the necessity of selecting one clearly defined direction for the first pathway to be cut through the unmapped wilderness of English scientific works, I have frequently suggested, but left unexplored, certain notable relationships between the ideas of the scientists and other important currents of Renaissance thought. Some of these interconnections between the new science and other movements—literary, philosophical, economic, and linguistic—I plan to develop more adequately in separate studies. Meanwhile, the material presented in this volume is offered in the hope that it will prove of timely and valuable assistance to others in similar studies of their own.
Because of the rarity of many of the works dealt with, I have made the practice of quoting liberally, believing that scholars would prefer to have the exact words of the original author rather than a summary which they could not readily check against a copy of the text itself. Also, I have included, at the end, a chronological list of English scientific books dealing with astronomy, and inserted therein a brief description of titles not mentioned elsewhere in this book.
Special mention should here be made of three earlier studies which have pointed the way to a few of the more prominent landmarks in the history of astronomy during the period covered by this book. Professor Dorothy Stimson’s The Gradual Acceptance of the Copernican Theory of the Universe (1917) provided many useful references to the advance of the new astronomical ideas on the Continent, and deserves recognition as an invaluable pioneering survey. But Miss Stimson barely touched upon the movement in England, merely noting that Recorde, Digges, and Gilbert were early supporters of Copernicus, [ix] and added nothing to our previous knowledge of the English writers. In fact, almost all references to the sixteenth-century English scientists which have found their way into the histories of astronomy and mathematics are traceable, in the end, to the works which two British scholars published nearly a century ago. On the one hand, William Whewell’s History of the Inductive Sciences (especially the third edition, of 1857), and on the other, the series of articles and books by Augustus De Morgan printed between 1836 and 1855 have been the basis, not only for the accounts in the Dictionary of National Biography of many of the Tudor mathematicians, but also for most subsequent allusions to their works. Because Whewell’s and De Morgan’s short notices were not followed up by more detailed studies of the books of the Elizabethan scientists, the trail which the two nineteenth-century scholars started so ably to blaze has gradually become overgrown with accumulated errors, some of them springing from the gaps or inaccuracies in their own information, but others from the mistakes of their followers who have carelessly used their work without verifying it by an examination of the sixteenth-century books themselves. Even though my own first-hand study of the early English scientific writings has revealed how sketchy and inadequate the material in Whewell and De Morgan often is, I have retained a genuine respect for their works, which, although not pretending to contain more than a brief survey of the scientific books printed in Tudor England, far surpass in completeness anything published between their time and the appearance of Professor E. G. R. Taylor’s Tudor Geography in 1930.
In the present volume I have chosen to avoid the laborious practice of cataloguing errors in Whewell and De Morgan, and in the historians of science who have followed them. Instead, I have preferred to cite the evidence of the original Elizabethan and Jacobean books for my statements, and to supply the reader with the material for making his own corrections.
Since the first draft of this study was written, two important works on closely related subjects have appeared. The first is [x] the series of articles by Professor Marjorie Nicolson on the telescope and the English imagination; the second is Professor R. F. Jones’s Ancients and Moderns. Both of these, however, have been centered upon the middle of the seventeenth century, whereas this work is centered upon the last part of the sixteenth. Readers will find that the three studies are, on the whole, supplementary rather than overlapping. Differences in emphasis and interpretation exist in our treatment of the seventeenth-century writers, but these are due principally to my having begun my investigations with a much earlier period, and thus approached from a different point of view the later material that we discuss in common. Rather than add a series of footnotes to my seventh and eighth chapters, to point out specific minor differences, I have thought it best to let the reader who so desires compare the three works as a whole, since the divergent angles from which our studies approach this material account for most of the dissimilarities in our interpretations. For the most part, however, our findings are in close agreement.
The collecting of much of the material for this study was made possible by the award of a Huntington Library International Research Fellowship in 1933. This enabled me to spend nearly two years working with that library’s superb collection of early English books, and to write the first draft of the present volume. A special grant from the American Council of Learned Societies gave me the opportunity to spend the summer of 1935 in England, supplementing my studies at the Huntington Library by examining the early scientific books that were missing from the Huntington collections. To the staffs of the British Museum, the Bodleian Library, the Mount Wilson Observatory Library, and the Huntington Library I wish to express my sincere appreciation for many courtesies and much useful assistance in my investigations.
I am particularly indebted to Dr. Edwin Hubble, of the Mount Wilson Observatory of the Carnegie Institution of Washington, for valuable criticisms and suggestions. The discussions we have had concerning the history of astronomy and [xi] the rare astronomical books he has so generously lent me from his own library have proved indispensable in my work. Other rare astronomical books placed at my disposal by Dr. George Ellery Hale greatly facilitated my investigations. The diagram of Tycho Brahe’s system of the universe is reproduced from Dr. Hale’s copy of the Progymnasmata with his kind permission.
I also wish to express my gratitude to my colleague as a Huntington Library Fellow, Dr. Sanford V. Larkey, now Librarian of the Welch Medical Library at The Johns Hopkins University. The opportunity which Dr. Larkey and I had for constant collaboration in our general studies in the history of Tudor science proved one of the greatest rewards derived from the fellowship.
Many other friends, former teachers, and colleagues at the Huntington Library have been kind enough to read the whole or parts of this study in manuscript, and to contribute helpful suggestions. To all of these I make grateful acknowledgment, and especially to Hardin Craig, Godfrey Davies, Ray W. Frantz, R. D. Havens, Theodore Hornberger, A. O. Lovejoy, G. B. Parks, Hazleton Spencer, Dorothy Stimson, and Louis B. Wright. For aid in checking the manuscript and reading the proofs I am obliged to Mr. M. H. Crissey, of the Huntington Library staff. But one of the greatest of my debts is to the Huntington Library research group as a whole, and to those who have assembled it—Dr. Max Farrand and the Trustees of the Library. Although the membership of the group is constantly changing, the enthusiasm for scholarship and the generous spirit of active co-operation which characterize it have already become part of an established tradition. Only one who has had the privilege of working daily as a member of the group can appreciate the aid and inspiration which it unfailingly contributes to his own endeavors.
Francis R. Johnson
Stanford University
January 30, 1937
Much has been written about the Copernican theory of the universe and its importance in the history of science. Almost every discussion of the literature of the late sixteenth and early seventeenth centuries has likewise had occasion to note its significance in the history of ideas and its influence on some of the outstanding writers of the period. In English literature, every consideration of the works of Donne, Bacon, or Milton, for example, is forced to take into account the new cosmology that was winning its way to universal acceptance at the time these men wrote. However, almost all treatments of the Copernican astronomy in its relation to the thought of the great Englishmen of the Renaissance have been permeated by the basic presuppositions of modern thinking. There has hitherto been no attempt at a thorough study of the new astronomy from the point of view of the English scientists living during the hundred years following Copernicus’ death.[1] Yet this point of view, and not our modern one, colored as it is by post-Newtonian science, determined the beliefs of the educated Englishman of the Elizabethan age when he turned his thoughts to the changing theories of the universe and the arguments advanced by the proponents of each system.
In this volume, therefore, I intend to examine the new astronomy and its progress in England up to 1645, as it appeared in the eyes of the men living at that time. I shall attempt, in so doing, to re-create a certain portion of the intellectual background of the English Renaissance, so as to lay the foundation for a better understanding of some of the ideas out of which its thought and literature were fashioned. In order to do this, it is essential to penetrate below the surface resemblances [2] between the notions of the present and those of the past, and to grasp fully the fundamental assumptions and basic problems which shaped the cosmological thought and philosophy of that age. The nature of the task may be better understood, and the difficulties more easily overcome, by first reviewing briefly the present-day habits of thought which tend to offer the greatest obstacles to an intimate understanding of the science of Elizabethan England.
To begin with, there is the great difference between the fundamental assumptions of that age and the present one. Unfortunately, almost all men tend to accept the basic presuppositions of their own times as irrevocably established principles, inherent in the very nature of things. Thus they incline to look patronizingly upon the men of an earlier period for their blindness in failing to perceive the self-evident “truth” of the propositions that came to be accepted by later generations. Nowhere is this attitude more noticeable than in the realm of the physical sciences. Yet, paradoxically enough, every sound philosophy of science emphasizes the fact that the so-called “scientific laws” are mere approximations, destined to be superseded as our knowledge of the material world increases. In short, these “laws” are no more than useful generalizations which assert a definite relationship between a number of diverse phenomena, and the true scientist accepts them only so long as they provide satisfactory explanations for the ever increasing body of observed facts. When they no longer can meet this test, these “laws” are either abandoned or modified. If we bear in mind this fundamentally hypothetical character of all scientific postulates and systems, we shall readily perceive the folly of condemning earlier scientific thinkers for accepting theories that were entirely tenable in the light of the facts then known, merely because the theories were overthrown by subsequent experimental discoveries.
Besides this tendency to regard our present scientific beliefs as immutable, and to censure past ages for not possessing our later knowledge, there is the modern habit of exaggerating the importance that science plays in the thinking, as well as in the [3] mere material surroundings, of the average educated man of today, and of minimizing the place of experimental science in the thought of the average Renaissance Englishman. That such an attitude is likely to be profoundly misleading will be amply demonstrated, I believe, during the course of the present study. We shall find that the interest in all phases of science was widespread in Elizabethan England, extending to all the literate classes. The number and variety of popular scientific books printed in the vernacular during this period provide one of the most significant phenomena of the age.[2] The quality of these popular books was, on the whole, remarkably high, and, with the possible exception of Italy, England saw more original works of significance in the history of science printed in the vernacular than any other country. This interest in science was not limited to a desire to master the traditional scientific ideas handed down from classical and medieval times. On the contrary, there was a universal eagerness to gain a thorough understanding of the principles underlying the new theories and discoveries, in order to turn them to practical uses for the further advancement of applied scientific learning.
That the scientific ideas, both new and old, which were current in the age of Elizabeth differed in many respects from those accepted at the present time is an obvious fact which must be frankly admitted. Nevertheless, it does not necessarily follow that these sixteenth-century ideas were essentially any less “scientific” from the historical point of view. In fact, we may find that they were grounded just as soundly upon the existing body of experimental observations as most of our modern theories. Today, it is true, a much larger body of evidence is available upon which to base our generalizations, and [4] therein lies, as a rule, the chief cause of the differences between our scientific beliefs and those of the scientists of the Renaissance. This is not to deny that many pseudo-sciences, erected upon a framework of false analogies, flourished in England during the Tudor and Stuart periods, just as the same, or very similar, pseudo-sciences still prosper among us. We would be making a serious error, however, to assume that the average literate Englishman of Elizabethan times was inferior to his twentieth-century descendant in his knowledge and intelligent understanding of the principles and problems of the science of his own day.
The foregoing remarks apply to the whole field of English science of the sixteenth and early seventeenth centuries. The present study, however, must necessarily confine itself to one special phase of the science of that period, for all the aspects of the larger field certainly could not be treated adequately within the limits of a single volume. Therefore, the progress of the new Copernican astronomy has been selected as the logical subject for thorough investigation, because it is the topic that is given the most prominent place in almost every modern discussion of the natural sciences in the English Renaissance. In these discussions, the new cosmology proclaimed by Copernicus is usually represented as the cause of an overwhelming change in our opinions concerning man’s importance in the universe and his relation to the external world. Before Copernicus, we are told, the earth and its human inhabitants were believed to be at the center of a small, compact universe, designed to minister to man’s needs. Today, largely owing to the change the new cosmology has wrought in our thinking, man has dwindled in importance to a position of insignificance in an infinite universe, in which the physical world is not only independent of man and his purposes, but is conceived as a huge mathematical machine which controls man’s actions and his ultimate destiny.
It is impossible to deny that this distinction between the ancient and the modern assumptions regarding man’s relation to nature is correct in many respects. On the other hand, it is [5] highly questionable whether this change in our thinking can justly be traced directly to the Copernican theory. Those who assume that the promulgation of the heliocentric system lies at the root of this intellectual transformation usually reveal that they are viewing the question in the light of present-day presuppositions. These modern ideas have been dominated by the axioms of Newtonian science and metaphysics, in which the Copernican hypothesis merely furnished the starting point for a mathematico-mechanical explanation of the motions of the planets in our own solar system.
There were, however, many other elements besides the Copernican astronomy which went into the making of the Newtonian philosophy of science.[3] First among these elements was the strong and significant revival, in the fifteenth and sixteenth centuries, of neo-Platonism, including those Pythagorean doctrines which emphasized mathematics as the key to the secrets of philosophy. Later came the extension of the [6] mathematical method to the treatment of motion, in which Galileo and his followers were the leading figures. Galileo’s successful treatment of mechanical motions in mathematical terms, in its turn, gave an added impetus to the revival of the atomistic doctrines of Democritus and Epicurus. By means of the atomic philosophy men found it possible to explain mechanically the whole of the material world.
Only when this stage was reached, near the middle of the seventeenth century, did contemporary thinkers clearly realize that they must grapple with a new and inescapable problem: the nature of the human mind itself. Philosophers were forced to ask themselves how mental processes were to be differentiated from the phenomena of the material world. They were explaining the latter in terms of the motions of material bodies. To what extent, then, might the act of thinking be subject to mechanical laws and considered as the product of the motions of material particles in certain parts of the human body?
The philosophies of Descartes, Hobbes, and Henry More and the Cambridge Platonists offered different answers to the problem, and each exercised a powerful influence upon seventeenth-century thought. It is in this period, therefore, rather than at an earlier date, that the new science began to work a revolution in the philosophical conception of man’s relation to the external world. But the works of Descartes, Hobbes and the Cambridge Platonists first appeared in the fifth decade of the seventeenth century,[4] and consequently did not influence English thinking in the period covered by this study of scientific thought.
In fact, of the various elements which ultimately went into the making of the materialistic philosophy associated with the development of modern science, only one of those I have just mentioned played a significant role throughout the period covered in this book—namely, the Pythagorean and mathematical phases of Renaissance neo-Platonism. The ancient Pythagorean notions that the universe was fundamentally mathematical [7] in its structure and that there was a harmonious mathematical relationship underlying all natural phenomena were revived and emphasized in the writings of several of the Italian scholars of the fifteenth century. These beliefs profoundly influenced Copernicus, and, at a later date, had an even more obvious role in determining Kepler’s philosophy. There will be many occasions, in the course of the ensuing chapters, to note the prevalence of the same ideas in the writings of the English scientists. But English thought in the sixteenth century was not influenced by the other philosophical currents that united to create the metaphysical beliefs that became associated with the new science, because these currents had their source in the writings of such men as Galileo, Gassendi, Descartes, Hobbes, and Newton. The Elizabethan could not foresee the course that scientific and philosophical speculation was destined to take in the next few decades; his beliefs and attitudes were inevitably governed by that body of concepts brought to him through the accumulated learning of earlier ages and through the contemporary works with which he was familiar.
This brief analysis of the philosophical currents which ultimately determined the distinctive characteristics of modern scientific thinking, though in a measure a digression, has seemed necessary as a warning against the too frequent attempts to find in the promulgation of the Copernican system the original cause of the radical differences between the modern conception of man’s place in the universe and that of the fifteenth century. The heliocentric theory was merely a single phase in a general intellectual and scientific movement, whose sources can be readily traced back to antiquity, and whose complex cross currents involve many things entirely unrelated to the new astronomy. Nevertheless, the announcement of the Copernican hypothesis was undeniably one of the most significant events in the whole movement. The progress of the new cosmology, moreover, although not the controlling factor in the evolution of the modern philosophy of science, is intimately bound up with each stage in its development, and cannot be adequately [8] understood apart from this philosophic background. Therefore, while guarding against crediting Copernicus with too large a share in altering man’s fundamental conception of his universe, we may most profitably take the history of astronomy as the basis for a work illustrating the advance of modern science and the progress of English scientific thought in the sixteenth and early seventeenth centuries.
It is in this spirit, and with these ideas in mind, that the present study has been planned and undertaken. Other phases of scientific progress in England, interesting and significant in themselves, will be discussed only when their intimate connection with the new astronomy makes some reference to them absolutely essential. Attention will be focused almost wholly upon the changing picture of the universe drawn by the astronomy of the Renaissance, as older ideas were gradually modified by new theories and discoveries. The more general questions of scientific philosophy and the contemporary attitudes toward science will also be considered, but only when the knowledge of these matters will help to make the problems created by the new cosmology stand out before us in clearer perspective. Some of the reflections of these changing conceptions of the universe in the works of famous literary men of the period will be mentioned in passing merely by way of illustration. But this book is concerned only incidentally with the literary repercussions of the new astronomy; its main purpose is to trace the progress of astronomical thought among the English scientific writers. A thorough discussion of the influence of these cosmological ideas on literature demands a separate volume; but one of the essential preliminaries to such a literary study is a proper understanding of the attitudes prevailing in contemporary scientific circles. It is toward the latter end—more limited, yet no less important—that this work is directed.
The questions before us, then, are: first, How did the intelligent, educated Englishman of the sixteenth century, as he sought to frame his ideas in accordance with the science of his day, picture the universe revealed to him by contemporary [9] astronomy?; and, second, How, and by what stages, did his conception change as a result of the progress of astronomy during the hundred years following the publication of Copernicus’ De revolutionibus in 1543? Our answers to these questions will be based chiefly on the evidence gathered from a careful study of the popular scientific books printed in England during the period from about 1500 to 1645. For this reason, something further should here be said concerning the primary importance of the popular scientific books in the vernacular in determining the scientific ideas of the average Englishman of the Renaissance.
It was from these popular books, written in English, and not from the more learned and technical works in Latin, that the vast majority of Englishmen derived their knowledge of astronomy and the other sciences. The latter works were usually comprehensible only to the expert; the average sixteenth-century reader was no more able to understand the intricate mathematics of the Almagest or the De revolutionibus than his twentieth-century descendant is capable of mastering such a work as Einstein’s Special and General Theory of Relativity. The essential ideas underlying these great scientific treatises were, however, presented to the layman in works written in a simpler, less technical language which he could understand. Books devoted to the popularization of the current theories and discoveries in science bore almost as high a ratio to the total book production in the sixteenth and seventeenth centuries as they do today.[5] Then, as now, there was a wide variation in the quality of such books. Some were able and authoritative expositions, written by the most eminent scientists of the day, and would correspond to the books now being written by men like Eddington and Jeans. Others were popular textbooks, composed by thoroughly qualified teachers of science. Then, at the other extreme, there were handbooks hastily and unintelligently compiled by hack writers with little or no genuine [10] knowledge of their subjects. Such works readily found a publisher and a market solely because of the ever increasing interest in science. Their most striking modern counterparts are to be found in the Sunday magazine sections of American newspapers, or in the cheap handbooks or almanacs peddled by itinerant book agents.
The popular works in the vernacular, for all their divergence in quality, from authoritative best to incompetent worst, were certainly the most important factor in the dissemination of scientific knowledge and the shaping of scientific beliefs in the English Renaissance. Their influence was not confined to scholars, or to those who had studied at the universities, but extended throughout all literate classes. Moreover, even graduates of the English universities in the sixteenth century would normally have received very little instruction in the natural sciences, and usually turned to the popular books in order to acquire an understanding of the principles of these subjects. This was undoubtedly true for astronomy, which was not included in the course for the B.A. The student who went on to take the M.A. would, it is true, have been expected to attend lectures in geometry and astronomy. Unless he had the good fortune to come under one of the brilliant young mathematical scholars during the brief periods of their active connection with the university, the instruction received by the candidate for Master of Arts would nevertheless have been most superficial and elementary.[6] Indeed, the better textbooks in the vernacular were more up-to-date, and superior in scope and quality to those commonly used in the Schools.[7]
In discussing the teaching of the mathematical sciences in the English universities in the sixteenth century, one must bear in mind the fact that there were no professorships in these subjects at either Oxford or Cambridge until 1619, when Sir Henry Savile founded the Savilian Professorships of Geometry and Astronomy at Oxford.[8] This does not mean that no thorough instruction in astronomy was given within the universities before that date. It seems certain, however, that advanced work and teaching in the subject were not a part of the regular curriculum for the M.A., and that their occasional existence in the universities was entirely dependent upon the enthusiasm and enterprise of individual scholars on the faculties. In contrast with the usual perfunctory and superficial presentation of such astronomy as was required in the Arts course, these men often sought to inspire their pupils with their own keen interest in that science, and to carry them far deeper into the subject than was customary at the time.[9] Only one [12] faculty, before 1619, would normally undertake any advanced instruction in astronomy—namely, the faculty of medicine. Astrology played an important part in the medical practice of the sixteenth century, and it was necessary for the physician to be able to make astronomical observations and calculations. Therefore, astronomy was an essential, though subordinate, part of the curriculum for the degree of Doctor of Medicine. We shall find that many of the leading writers of popular books on astronomy were “Doctors of Physic.”[10]
From these facts we may conclude that, although the universities undeniably played an important part in the diffusion of astronomical knowledge in sixteenth-century England, their influence was confined to a comparatively small group of men. The majority, even among university students, acquired their detailed knowledge of the principles of astronomy, such as it was, wholly outside the regular university curriculum. We shall see, later, that they, too, usually turned to the popular books for their information.
The indirect influence of the universities was nevertheless significant. Most, though by no means all, of the writers of the best English treatises on astronomy were university men. It was their scholarly knowledge of Greek and Latin, gained at the universities during the periods of intense enthusiasm for classical studies, that enabled them to master and to criticize the great scientific works, both ancient and modern, and to embody the results of their labors in sound and thorough treatises on science, written in English for the benefit of their less learned countrymen. Moreover, the scientists who were connected with the universities had often, because of their enthusiasm for astronomy, carried on advanced, independent studies while resident at Oxford and Cambridge. We have already noted that such men, when they remained as fellows and tutors of colleges after incepting as M.A., often transformed their “ordinary lectures” into up-to-date, advanced courses in mathematics [13] and astronomy. The students who showed an eagerness for further knowledge in the sciences doubtless received much encouragement and special instruction from these tutors. It was through this personal, master-and-scholar arrangement, rather than as an organized part of the university course, that scientific and astronomical studies were carried on, in certain instances, at Oxford and Cambridge. Prior to 1619, however, when these subjects received their first official recognition and support, most of the able scientists did not long remain within the universities, but transferred their activities to London.[11] As a result, scientific studies at those two centers of learning made no steady progress, but were marked by intermittent periods of brilliant individual activity.
Inasmuch as the influence of the universities in the dissemination of modern astronomical knowledge was centered almost entirely in the work of a few outstanding men, the ideas and the teachings of these leaders must constitute a second principal source of information concerning astronomical thought in England during the Renaissance. This source, and the first, tend to merge into one whenever an eminent scientist from one of the universities published a treatise in English dealing with astronomy. But not all of the prominent leaders in scientific studies wrote popular works on their subject; moreover, some of the most important popular writers were never connected with either university. Yet, because they were so famous in their own day that their contemporaries recognized them as the most learned authorities on the mathematical sciences, their knowledge and beliefs would have considerable weight in determining the attitude of their friends and pupils towards any new hypothesis or discovery. Their influence would thus be very great among all scientific workers, and would profoundly affect the character of popular beliefs, both directly and indirectly, through treatises written by others of their circle.
Our inquiry into the progress of the new astronomy in England therefore presents two different, but closely related, aspects. The first has to do with the opinions, at different periods during the century after Copernicus, of the leading English mathematicians and astronomers—the men to whom intelligent laymen of the time would turn for expert judgment in such technical matters. The second concerns the popular presentation of the science of astronomy in the books printed and sold in England during the Renaissance. From this twofold study and analysis of the ideas of the outstanding scientists, and of the popular astronomical treatises, we should get an insight into Elizabethan thought which will enable us to see the new theory of the universe proposed by Copernicus as it appeared to the eyes of the Englishman of the sixteenth and seventeenth centuries.
The following chapters will therefore present a brief history of astronomical thought in England from the beginning of the sixteenth century to the year 1645. First will come an analysis of the elements entering into the pre-Copernican conception of the universe, for without a clear understanding of the essential features of this earlier system one cannot read the sixteenth-century astronomical treatises with any accurate perception of their true meaning or implications. Particularly important is a knowledge of the scientific and philosophical bases for the various details which were incorporated in the old cosmology, and this can best be attained through a brief survey of the history of earlier astronomical theories and systems. Such a survey has the advantage of familiarizing us with the ideas of the scientific writers most often cited in Renaissance texts, and presenting to us the leading figures in the development of astronomy as they appeared to English readers in the sixteenth century. Subsequent chapters will then take up the tracing of cosmological ideas in England, dealing, in turn, with astronomical books and scholarship prior to 1543; with the intrinsic relationship of the heliocentric system to the older system based on Aristotle and Ptolemy, and the exact scientific and philosophic impact of the Copernican theory; and with the course [15] of astronomical thought among English scientists throughout the century following the publication of the De revolutionibus. The four chapters devoted to the period from 1543 to 1645 will carry this study to the middle of the decade in which the group of English scientists who later organized the Royal Society began their meetings in Oxford and London. This decade can most fittingly be taken to mark the end of a most significant era of some one hundred and fifty years, which witnessed the transition from medieval to modern science.
The theory of the universe finally overthrown by Copernicus, but generally accepted throughout Europe in the sixteenth century, is commonly termed the Ptolemaic system. Such a designation, attributing to Ptolemy the ideas which made up the current conception of the world revealed by astronomy, is in many respects quite misleading. The cosmological doctrines prevailing before 1543 actually owed far more to Aristotle than they did to the author of the Almagest. The medieval and Renaissance writers, it is true, constantly quoted Ptolemy as the principal authority for the ideas they set forth concerning the construction of the physical universe. Few, however, had ever read Ptolemy’s great Syntaxis—popularly called the Almagest, from an abbreviation of its Arabic title. Fewer still were capable of mastering his complicated mathematical constructions, whereby the planetary motions were represented by means of combinations of eccentric circles and epicycles. Any real understanding of Ptolemy’s important work was therefore largely confined to the mathematicians who calculated the tables of planetary positions published in the ephemerides. For explanations of the physical constitution of the heavens, popular writers continued to turn back to Aristotle and his system of homocentric spheres.
The pre-Copernican cosmology, therefore, can best be characterized as a combination of the physical theories of Aristotle with the mathematical constructions of Ptolemy. To the divergent elements already included in this union, many writers added a generous mixture of neo-Platonic and Christian mysticism. The conception of the universe which resulted from the fusion of these various elements presented several striking inconsistencies and logical dilemmas which were usually overlooked in medieval times. This situation was quickly altered [17] when, with the revival of learning in the Renaissance, men began to have a far wider knowledge of the ideas of the early Greek philosophers. The more enterprising thinkers of this period commenced to compare the older cosmological speculations with the accepted system of their own times, and discovered that no feature of this system had gone unchallenged among ancient writers, but that each detail had encountered able opponents who had advanced plausible arguments in favor of a different theory.
As a result of the recovery of many of the works of the Greek scientists, fifteenth- and sixteenth-century Europe was witnessing, even before the publication of Copernicus’ De revolutionibus, a revival of bitter disputes concerning the nature of the universe—disputes in which the long-forgotten ideas of the early philosophers began once more to play a prominent part. Democritus, Plato, Heraclides, Epicurus, Plotinus, and many others were quoted by one faction as authorities equal to Aristotle, and their statements violently attacked by the opposing party. Consequently, some knowledge of the history and scientific basis of the various cosmological theories and systems, from Greek times down to the sixteenth century, is absolutely essential to any real understanding of Elizabethan discussions concerning the nature of the physical world.
Before proceeding to summarize the most significant features of the history of astronomical thought prior to Copernicus, however, it would be well to consider for a moment the salient facts regarding the apparent motions of the heavenly bodies. A clear perception of these facts is necessary to our study, for they are the foundation upon which any system of the universe worthy of scientific attention must be erected. Astronomical theories, throughout history, have become more complicated in direct proportion to the number and complexity of the stellar motions that man has observed. Before the days of the telescope, only the features of the heavens visible to the naked eye had to be taken into account. Many of these might well have been noted from earliest times, for they could have been discovered by anyone who made intelligent and systematic observations [18] of the sky over long periods of time. Others required the use of instruments for accurately determining the relative positions of the stars, and the aid of mathematics in plotting their courses. As more precise instruments were developed, and as the recorded observations were multiplied, slight inequalities in the apparent motions of the sun, moon, and planets were perceived, whereas, before, these motions were thought to be uniform. These new inequalities had then to be considered by the mathematical astronomer in framing his theories and making his calculations.
There is always, therefore, a direct relationship between the progress of systematic observation of the stars and the astronomical system designed to account for the facts which current investigations have brought to light. This comment applies not only to the state of the science of astronomy in any age, but to the beliefs held by any individual at any period in history. The nature of the cosmological system which will seem reasonable and satisfactory to a given person—be he living in the second century or the twentieth—will be determined by the variety of the stellar motions which he has himself observed, or knows about and accepts on the evidence of others’ observations. Were this not so, we should not find people today, like Voliva and the members of the community of Zion City, persisting in the belief that the earth is flat, when the definite manner in which the meridian altitudes of the stars vary with the latitude of the observer completely invalidates such an idea; only persons who are ignorant of the way in which the positions of the stars vary as one travels north or south, and who are unfamiliar with the principles of geometry, can believe in a flat earth.
From what we have just said, it is apparent that the order in which the elementary facts concerning the motions of the heavenly bodies are likely to be first perceived by a careful observer can furnish a most useful key to the evolution of cosmological theories. Undoubtedly, the daily motion of the sun was the astronomical phenomenon which first attracted man’s attention, and primitive peoples all have some mythological account [19] which gives a reason for it. The Greek legend of Apollo, the sun-god, driving his golden chariot across the sky is the most familiar example. The movements and phases of the moon were probably the next features for which our ancestors sought explanations. The exact order in which other prominent details of the motions of the stars and planets were first noticed is, of course, purely conjectural, and may have varied with different nations; but the sequence set forth in the following paragraphs seems more likely, on the whole, than any other. In general, it almost certainly agrees with the order in which early astronomical discoveries have usually been made.
Primitive peoples, in the beginning, attempted to explain nothing beyond the daily journeys of the sun and moon from east to west across the sky. Then, the regularly recurring phases of the moon were noticed, and reasons invented to account for them; but it was probably not until much later that man perceived that the moon’s phases bore a definite relationship to its position with respect to the sun. Before this comparatively advanced observation was made, however, some sort of systematic effort to trace the courses of the stars must have been made among ancient races. In that case, certain other facts could not have escaped notice. It would have become clear that the stars, as well as the sun and moon, had a diurnal motion from east to west across the heavens; that the sun pursued a wandering course among the stars, being higher in the heavens in summer than in winter; and that it returned at the end of a year to its original position, and the cycle of the seasons then began anew.[12] The moon, too, would have been seen to wander among the stars, following a path very similar to the sun’s, but traveling much faster, so that it completed its circuit of the [20] heavens in about twenty-seven days; two more days, making twenty-nine, were required for it to overtake the sun, which had moved forward in its course in the meantime. Then another cycle of the moon’s phases began. The stars themselves would have been observed to travel nightly across the sky, rising in the east and setting in the west, just as did the sun and the moon. Some of the stars, however, never disappeared below the horizon, but circled in a counterclockwise direction about a fixed point in the northern heavens very close to the prominent star that we call the Pole Star.
It obviously required a certain degree of careful and continued study of the heavens for man to recognize these details of the stellar motions. Perhaps not one person in a hundred living today has discovered for himself even these elementary facts of astronomy. Had he done so, he would realize that, once the circular paths of the circumpolar stars were fully comprehended, it was only natural to infer that the stars were situated in a huge sphere revolving about the earth. The idea that the movements of the heavens might be represented and calculated geometrically followed as an inevitable consequence.
When this point was reached, astronomy began to be a genuine science. The courses of the stars in the heavens were now thought of as phenomena determined by definite, mechanical laws, which painstaking research might well reveal to mankind. Therefore, the early astronomers began methodically observing and recording the relative positions of the stars from night to night throughout long periods of years. By this means they readily confirmed the fact of the apparent daily rotation of the celestial sphere about an axis, one of whose poles was located near the star Polaris in the constellation of Ursa Minor. The path of the sun across the heavens was found to differ greatly from the equator of this sphere; in fact, it lay along a great circle making an angle of between twenty-three and twenty-four degrees with the celestial equator.[13]
Men had already noted that the sun’s position among the stars changed about one degree each day, and this had formerly been explained by the hypothesis that the sun was attached to a sphere moving about the earth in the same direction as the stars, but not quite so rapidly as the stellar sphere. Once the inclination of the sun’s orbit to the celestial equator was fully understood, the abler mathematicians saw that this theory would not suffice, and promptly altered it. They made the axis of the sun’s sphere differ from that of the sphere carrying the stars, and gave the solar sphere a motion of its own in a direction opposite to the daily rotation of the heavens. Thus the sun’s movement was pictured as a combination of a diurnal rotation from east to west, produced by the force of the heavenly sphere, and of its own, slower motion from west to east, the latter motion resulting from the rotation of the solar sphere, and requiring a year for its completion. A similar theory accounted for the movements of the moon; but the moon’s proper motion from west to east was, of course, over twelve times as fast as the sun’s, so that it traversed the heavens, in a direction contrary to the daily motion of the stars, in slightly over twenty-seven days, the length of its sidereal period.[14]
Meanwhile, certain facts about the heavenly bodies were undoubtedly being noticed by the ancient astronomers. Careful comparison of successive observations of the stars clearly proved that, except for five of their number, their relative positions remained absolutely unchanged. Thus all the others could well be regarded as placed on a single, rotating sphere, which was accordingly termed the sphere of the fixed stars. The five wandering stars, or planets,[15] required special consideration. When these had been followed for several decades in their journeys around the heavens, their paths were discovered [22] to be in approximately the same plane as that of the sun—that is, the plane of the ecliptic. The speeds of the planets differed, however. Saturn took almost thirty years to return to its original position among the stars; Jupiter, twelve years; Mars, slightly under two years. Venus and Mercury had sidereal periods of about one year, corresponding to the sidereal period of the sun, which both of them followed very closely in its course about the heavens, Venus never appearing more than some forty-six degrees from the sun, and Mercury never more than twenty-four degrees. Consequently, the early astronomers provided each of these five planets with a sphere which carried it around the sky in a direction contrary to the motion of the sphere of the fixed stars, at a rate corresponding to the planet’s sidereal period.
Inasmuch as the courses of the moon and the five planets in the heavens never wandered greatly from the circle representing the sun’s path among the stars, it was natural enough for the ancients to use this ecliptic circle as a base to which all planetary motions might be conveniently referred. Hence arose the system of locating the stars, and more particularly the sun, moon, and planets, by means of the signs of the zodiac. The zodiac was merely an imaginary band encircling the heavens, extending six degrees on either side of the ecliptic circle, so that its total width was twelve degrees—just sufficient to contain within its limits the courses of the moon and the planets.[16] It was divided into twelve equal parts, of thirty degrees each, so that each part corresponded to the distance that the sun traveled among the stars during one month and was approximately equal to the distance between the points in the heavens at which two successive like phases of the moon occurred. The first of these twelve divisions began at the point at which the sun, in its northward course among the stars at the beginning of spring, crossed the celestial equator, this point being known as the vernal equinox. Each thirty-degree [23] section of this band about the ecliptic was named after a prominent constellation lying within its limits—hence the twelve signs of the zodiac. In order, beginning with the vernal equinox,[17] the names of these signs are: Aries (the Ram), Taurus (the Bull), Gemini (the Twins), Cancer (the Crab), Leo (the Lion), Virgo (the Virgin), Libra (the Scales), Scorpio (the Scorpion), Sagittarius (the Archer), Capricornus (the Goat), Aquarius (the Water Carrier), and Pisces (the Fishes).
For the purposes of ancient astronomy, which came to a high stage of development among the Greeks, the ecliptic system of reference points and lines was probably more satisfactory than any other would have been. Early astronomers were interested almost exclusively in the movements of the sun, whose path was the ecliptic circle, and of the moon and planets, whose positions were always very close to that circle. Although in modern times star positions are usually referred to the celestial equator, the ecliptic system, using the signs of the zodiac, continued in favor among astronomers until long after Copernicus, and is the only one we need consider in our study.
Once a definite system of co-ordinates had been adopted by ancient astronomers, more rapid progress in that science became possible. Positions could now be described more accurately, and observations taken in one locality could be used by other astronomers at different places throughout the ancient world. With the increasing scientific interest in astronomy, more precise instruments were gradually developed for measuring [24] the angular distances between heavenly bodies, and methodical observations were taken over longer periods of time. As a result, additional facts concerning the motions of the planets were soon discovered. First, no doubt, the inclination of the moon’s orbit to the ecliptic was measured, and the cause of eclipses became known when it was determined that these phenomena occur only when the moon is near those points at which its orbit intersects that of the sun. The inclinations of the other planetary orbits were also calculated, for systematic observations soon revealed that the planets did not follow the exact path of the sun, but varied in latitude, appearing sometimes north and sometimes south of the ecliptic.
By similar methods, the progressive and retrograde movements of the five planets were discovered. We now explain these movements as the result of the earth’s orbital motion about the sun, which causes the other planets, which are likewise circling about the sun, to undergo changes in the direction of their movements, as seen by observers on the earth. To the terrestrial onlooker, each planet, after moving forward in its normal direction for a certain space of time, appears to proceed more slowly, then to remain stationary for a day or two, and after that to go backward among the stars for a period. When it reaches the end of its retrograde arc, which is always shorter than the advancing one, it again remains stationary for a short while, after which it begins once more to progress in its normal direction.
It can readily be seen that the discovery of the retrograde movements of the planets placed insurmountable obstacles in the way of any simple, geometrical representation of all the stellar motions. The neat system of seven concentric spheres encircling the earth could no longer suffice for scientific astronomers, because it could not possibly be made to account for the facts. The inadequacy of any such simple cosmology was emphasized by the variations noted in the brilliance of the planets. Mars, in particular, was far brighter when in opposition to the sun, and Venus when in conjunction. The logical interpretation of this phenomenon was that the planets were not always at the same distance from the earth.
The difficulties already present were greatly multiplied when it became evident, from comparisons of the recorded positions of the sun and moon, that these bodies did not move with uniform velocity in their orbits, but advanced more swiftly at some seasons than at others. Still further complications arose after the precession of the equinoxes was determined by Hipparchus in the second century B.C.[18] By comparing his observed positions for certain fixed stars with those made by Timocharis some one hundred and fifty years earlier, he noted that the recorded longitudes of all these stars had changed by the same amount—about two degrees. Hence he concluded that the equinoxes (the two points at which the celestial equator intersects the ecliptic) had slightly changed their positions among the stars during this interval. Although Hipparchus’ discovery does not seem to have become universally known in the ancient world, it was accepted and used by Ptolemy, and all of the ablest astronomers of succeeding ages were forced to take it into account.
As more precise instruments were made and used, other slight inequalities were found in the planetary motions, but we have already pointed out the ones that were the most important and troublesome. The problem presented to astronomers, from ancient times down to Copernicus—and indeed to the time of Newton—was, first, to devise a system which would represent mathematically the motions of the heavens without introducing any assumptions inconsistent with the known facts; and, second, to seek out physical causes which would explain these motions. The history of astronomy, therefore, is largely an account of the successive attempts to solve these problems, and of the conflict between the earlier, oversimplified cosmological systems, and those which endeavored to represent accurately every known variation in the movements of the stars and [26] planets. We have already observed that the approach of the ancient astronomers to these problems was truly scientific in its spirit; theories were devised to account for observed facts, and were modified when further observations made changes necessary. The Renaissance astronomer realized this; he was familiar with the ideas of the earlier scholars who had made notable contributions to the science of the stellar motions, and often cited them in his writings, though reserving the right to disagree with certain details of their theories. To look upon the contemporary state of astronomy with his eyes, therefore, we must first review the history, as he knew it, of the development of cosmological systems up to the mid-sixteenth century, noting as we proceed the leading names associated with the introduction of each important element of the usual pre-Copernican conception of the universe.
The well-known reverence for the authority of Aristotle in the late Middle Ages and the earlier years of the Renaissance might seem, at first thought, a compelling reason for beginning with an account of the Aristotelian cosmology. Aristotle, however, was preceded in ancient Greece by several important philosophers and scientists. Wherever his system is based upon the ideas of his predecessors, special consideration of their theories is unnecessary, for it was chiefly through Aristotle that their views were known to sixteenth-century Europe. There were, on the other hand, important schools of early Greek philosophers with whom Aristotle violently disagreed, and large sections of his scientific treatises are given over to attempts to refute their doctrines. The late Middle Ages knew of these earlier ideas chiefly through Aristotle’s prejudiced accounts of them. The significant revival of neo-Platonism in the fifteenth century, with the consequent reawakening of interest in the cosmological theories of Plato and the pre-Socratic philosophers, thrust these older ideas into the main current of European thought. An understanding of certain features of the pre-Aristotelian cosmological systems is therefore essential to our study.
We may safely neglect the primitive notions of the earliest [27] Greek thinkers, and begin with the atomic theory of Leucippus and his more brilliant disciple, Democritus, who lived in the fifth century B.C.[19] The planetary system expounded by these philosophers was a comparatively crude one, for clearly they did not have at their disposal any large body of methodical observations of the motions of the planets. It is the physical theories of Democritus that are important, rather than the details of his planetary system. He believed that the entire universe consisted of an infinite number of extremely small, indivisible, finite bodies, termed atoms, which moved in a void. Everything had its cause in the movements, combinations, and separations of these atoms. In infinite space, this infinite number of atoms produced an infinite number of worlds, which were subject to continual change. When two worlds collided, they perished. When our own universe began to be generated by a collocation of atoms, a kind of skin was formed around it, which by degrees became thinner as parts of it settled to the middle, owing to the vortex motion. The earth was formed of some of these particles, while others produced the fire and air that fill the space between earth and heaven. Some of the atoms, caught by the spherical outer membrane, crowded together into compounds, which finally caught fire, thereby producing the stars. Democritus believed that the number of universes similar to ours was infinite, and also had a correct conception of the nature of the Milky Way, the light of which he attributed to a multitude of very faint stars.
Democritus’ fame in the Renaissance for the atomic theory of matter and the idea of infinite worlds was paralleled by the [28] renown of the Pythagorean school of philosophers for their hypotheses concerning the arrangement and relative motions of the planets. Indeed, the reputation of the Pythagoreans was not related solely to their planetary theories, but embraced their entire philosophy, with its emphasis upon a mystical reverence for numbers. To them, number was not merely a representation of the relations between phenomena, but the very substance and cause of everything in the physical world. The universe itself was the product of harmonious mathematical relationships. The Pythagoreans, therefore, assigned to mathematics the foremost place in their philosophical system. It was thus only natural that they should take the lead in applying mathematics to the study of astronomy. Ancient writers attribute either to Pythagoras himself (sixth century B.C.) or to certain of his followers most of the important early discoveries of the nature of the world, such as the spherical shape of the earth, the fact that the morning and evening stars are one and the same, and that the moon shines with the reflected light of the sun. Alcmaeon, one of the Pythagoreans, pointed out that the planets move in separate orbits from west to east in a direction contrary to the fixed stars, thus superseding the older idea that they traveled from east to west, only somewhat more slowly than the stars.
After the discovery of the separate orbits of the sun, moon, and planets, the Pythagoreans doubtless felt it to be a flaw in the harmonious mathematical arrangement of the universe that the entire heavens should be rotating in the opposite direction. Consequently, they invented a system that had as its central feature the idea that the apparent daily rotation of the stars and the daily motion of the sun were caused by the earth’s being carried around the circumference of a circle once every twenty-four hours. The credit for the development of this system is usually given to Philolaus, a Pythagorean who lived at the end of the fifth century, and was therefore a contemporary of Socrates. Philolaus evidently perceived that, if the earth had an orbital motion with a period of twenty-four hours, the terrestrial observer would see the entire heavens make an apparent [29] revolution during the course of a day and night, and that in this arrangement all real motions would take place in the same direction, from west to east. The notion that the earth might be conceived as rotating about its own axis seems never to have occurred to Philolaus, although, as we shall see presently, later members of the Pythagorean school advanced the doctrine of the earth’s rotation.
In the Philolaic system, the earth did not occupy the central position in the universe. That place was assigned to a “central fire,” about which the earth and all the planets, including the sun and moon, revolved. This “central fire” caused a great deal of confusion, in later times, among medieval and Renaissance writers. Many of them totally misunderstood the nature of the system of Philolaus and mistakenly assumed that this “central fire” was the sun. Hence, in the sixteenth and seventeenth centuries, Copernicus was constantly referred to as a champion of the ancient doctrines of the Pythagoreans, because he made the earth revolve about the sun.[20] This error was never made by Copernicus himself, who seems to have rightly understood the nature of the Philolaic system, and to have known that the ancient accounts of it agreed in stating that the sun, as well as the earth, moved around the “central fire.”
The Pythagoreans explained the fact that no one had ever seen this “central fire” by maintaining that the known parts of our globe were all situated on the side of the earth which is always turned away from the center of its orbit. It would therefore be necessary to travel beyond India to view this mysterious fire, and even then it would be impossible to observe it, because another planet intervened between it and the earth. This hypothetical, unseen planet was given the name of the antichthon, or counter-earth, and was believed always to keep pace with the terrestrial globe. Doubtless the Pythagorean reverence for ten as the perfect number, comprising in itself [30] the whole nature of numbers, was responsible for the invention of the antichthon, in order that the total number of bodies encircling the “central fire” might be brought up to ten. These bodies would then be, in order from the center outward, the antichthon, the earth, the moon, the sun, the five planets, and the sphere of the fixed stars.[21] Aristotle gives a clear exposition of the Philolaic system,[22] as does Simplicius in his commentary on the De Caelo. Further interesting details are set forth in Aëtius’ epitome of the history of early Greek philosophy, showing the threefold division of the universe made by the Pythagoreans:
Philolaus calls the fire in the middle about the centre the Hearth of the universe, the House of Zeus, the Mother of the Gods, the Altar, Bond and Measure of Nature. And again he assumes another fire in the uppermost place, the fire which encloses (all). Now the middle is naturally first in order, and round it ten divine bodies move as in a dance, [the heaven] and <after the sphere of the fixed stars>, the five planets, after them the sun, under it the moon, under the moon the earth, and under the earth the counter-earth; after all these, comes the fire which is placed like a hearth round the centre. The uppermost part of the (fire) which encloses (all), in which the elements exist in all their purity, he calls Olympus, and the parts under the moving Olympus, where are ranged the five planets with the moon and the sun, he calls the Universe, and lastly the part below these, the part below the moon and round the earth, where are the things which suffer change and becoming, he calls the Heaven.[23]
From this passage it is clear that the lowest division of the Pythagoreans—the Heavens, or Ouranos, lying below the moon and containing all things subject to change and decay—agrees with the lower of Aristotle’s two divisions of the world. But above the moon the Pythagoreans placed two regions instead of one. With them, the sphere of fixed stars was the boundary between the Universe, or Cosmos, and the Olympus, which contained the outer fire surrounding the stellar sphere and was the place of the elements in their greatest purity. Surrounding the Olympus was infinite space, or the infinite air from which the world draws its breath.
It is interesting to note that, whereas the Pythagorean system did not definitely include the infinite worlds of Anaxagoras and Democritus, it did nevertheless picture an infinite region beyond the sphere of the fixed stars. This became especially important when the neo-Platonic philosophy, with its strong Pythagorean element, was revived in the Renaissance, for therein the fifteenth-and sixteenth-century philosophers found ancient authority for portraying a universe at once finite and infinite.
The Philolaic system truly marked a great advance in man’s attempts to account satisfactorily for the apparent motions of the heavens. It explained many phenomena in a much better fashion than the earlier theories. It provided reasons for the apparent rotation of the stellar sphere, for the recurrence of day and night, for the revolutions of the moon and planets, and for the motion of the sun in the zodiac.[24] Of course, it failed to account for the irregularities in the motions of the planets, but so did the simple geocentric system, and probably these irregularities had not yet been fully recognized in the time of Philolaus. Another, and greater, difficulty was that the motion of the earth, as the Philolaic system pictured it, ought to have caused a considerable variation in the apparent diameters of the sun and moon during the course of a single day, because those bodies had their orbits nearest the earth. To [32] overcome this objection, the distances of the antichthon and the earth from the “central fire” were assumed to be exceedingly small in comparison with the distances of the moon and sun.
The presence of this difficulty, however, together with their inability to prove the actual existence of the “central fire” and the antichthon, led later members of the Pythagorean school gradually to give up the Philolaic in favor of a geocentric system, transferring the “central fire” to the middle of the earth and eliminating the antichthon. Once this was done, the next logical step was to portray the earth as rotating about its own axis every twenty-four hours. We know for certain that this step was actually taken by Heraclides of Pontus (circa 388-310 B. C.), a contemporary of Plato and Aristotle, who, if he had not actually studied with members of the Pythagorean school, as asserted by Diogenes Laertius, was at least thoroughly familiar with their cosmological doctrines. Ancient writers also mention one Hicetas of Syracuse, and one Ecphantus of the same city, both styled Pythagoreans, who maintained that the earth rotated on its axis. Nothing further is known about the scientific ideas of these two men, and their lives are a complete mystery. It has been suggested that Hicetas and Ecphantus are merely the names of characters in some lost dialogues on scientific subjects written by Heraclides himself.[25] The writers of the Renaissance, however, knowing the ancient references to these two men, always list them together as Pythagoreans who gave their authority to the idea of the rotation of the earth.
Heraclides of Pontus also taught that the universe was infinite, that each star was a universe or world, suspended in the infinite ether, and comprising an earth, an atmosphere, and an ether. He maintained that the sun, not the earth, was the center of the orbits of Venus and Mercury. Although Ptolemy did not adopt this idea in his system, it was recorded by many ancient writers, notably by Vitruvius and Martianus Capella, and also by Macrobius in his commentary on Cicero’s Somnium [33] Scipionis. Thus the knowledge of this hypothesis was current throughout the Middle Ages, for the works just mentioned were among the most familiar and popular Latin writings during that period.
Aristotle, at the time of the writing of his De Caelo, apparently was not acquainted with the ideas of his contemporary, Heraclides. Otherwise, he certainly would have taken some notice of them, if only to set forth arguments against them, as he did against the atomic theories of Democritus and the planetary system of Philolaus. Before turning to Aristotle’s cosmological doctrines, however, something should be said concerning the ideas of his master, Plato. Also, a brief exposition of the mathematical system of homocentric spheres developed by Eudoxus and Calippus must be given, because Aristotle adopted their system and made it a part of his cosmology.
Plato’s theories concerning the construction of the universe are to be found chiefly in the Timaeus, and in the last part of the tenth book of the Republic, although scattered references occur in his other works. An extensive discussion of the cosmological ideas advanced in these books would be out of place in the present study. However, because of Plato’s enduring fame and the wide influence of his writings in the Renaissance, an understanding of the main features of his picture of the universe is essential, in order to note wherein he agreed with or differed from his predecessors among the Pythagoreans, on the one hand, and from Aristotle, on the other.
There is no doubt of Plato’s thorough familiarity with the chief ideas of the Pythagorean school, nor of the great influence that their theories had in the formation of his own philosophy. Plato’s high regard for mathematics and his tendency toward a mystical reverence for numbers were derived from this source. In fact, the dissemination of the Pythagorean beliefs was primarily due to Plato, in whose universally popular writings the doctrines of these earlier thinkers were sympathetically discussed and, in many instances, definitely adopted. In cosmology Plato contributed greatly to the spread of their teachings concerning the spherical figure of the earth and the [34] orbital motion of the planets from west to east, contrary to the apparent motion of the fixed stars. While accepting these two features of the Philolaic system, he did not adopt it in its entirety. Instead of picturing the earth as revolving in a circle about the “central fire,” he taught that the earth was motionless in the center of the universe and that the heavens revolved about the earth once every twenty-four hours. Because of a difficult, often disputed, passage in the Timaeus,[26] many writers have claimed that Plato there set forth the idea of the daily rotation of the earth in order to account for the apparent motion of the heavens, but most modern authorities have concluded that there is no justification for so construing the passage.[27] A misinterpretation of this section of the Timaeus by Renaissance authors, however, could well have led them to consider Plato as one of the ancient authorities favoring the theory of the earth’s rotation.[28]
Plato’s system may therefore be described briefly as follows: in the center was the motionless earth, about which the firmament revolved once every twenty-four hours, carrying the planets with it. The planets, however, had their own separate orbits, in which they traveled in a direction opposite to the sphere of the fixed stars. Plato placed the planets in an order corresponding to the relative speeds with which they completed their circuit of the heavens, and assigned distances to them proportional to the figures derived from the two geometrical progressions, [35] 1, 2, 4, 8, and 1, 3, 9, 27. His order, therefore, was: Moon, Sun, Venus, Mercury, Mars, Jupiter, Saturn. The sun, Venus, and Mercury were grouped together because they completed their revolutions in the same period—one year; but Plato noted that they at times moved in a direction contrary to that of the sun.[29] He was also aware that the motions of the planets were more intricate than such a simple system could fully explain. He says:
Of the other stars [except the sun and moon] the revolutions have not been discovered by men (save for a few out of the many); wherefore they have no names for them, nor do they compute and compare their relative measurements, so that they are not aware, as a rule, that the “wanderings” of these bodies, which are hard to calculate and of wondrous complexity, constitute Time.[30]
On the much disputed question of whether there was an infinite number of worlds, or only a single, finite universe, Plato takes his stand in favor of the latter hypothesis.[31] But after referring to the ideas of the atomists, he goes on to say that whether one should describe the world as one, or as five, is a debatable question. This is the starting point for his description of the four elements, in which he adopts a number of the atomistic ideas. To each of the four elements he assigns one of the regular solids as the proper form for its particles. These elements, because of their differences in weight and stability, have a tendency to group themselves about the earth in concentric spheres. Earth, of course, is in the center, then comes water, then air, and lastly fire. Beyond the sphere of fire lie the planets and the stars, composed of a fifth element which corresponds to the dodecahedron and is the most perfect element, since its figure most nearly approximates the sphere. It is therefore the appropriate constituent of the bodies having circular motions.
In the Timaeus, all the heavenly bodies are looked upon as divine beings, and this animistic character of Plato’s system is seen in his portrayal of the universe as the home of a hierarchy [36] of spirits, the lowest being those whose habitation is the earthly region, and the highest dwelling in the changeless heavens.[32] One other point must be mentioned. In Plutarch’s life of Numa, the author says, speaking of the Pythagoreans’ doctrines:
For they are of opinion, neither that the earth is unmoveable, nor yet that it is set in the middest of the world, neither that the heaven goeth about it: but saye to the contrarie, that the earth hanged in the ayer about the fire, as about the center thereof. Neither will they graunte, that the earth is one of the first and chiefest partes of the world: as Plato helde opinion in that age, that the earthe was in another place then in the very middest, and that the center of the world, as the most honorablest place, did apperteine to some other of more worthy substaunce than the earthe.[33]
It is interesting to note that Thomas North, in his translation, made Plato’s adherence to the Philolaic system even more explicit than had Plutarch himself. The latter had merely said that it was reported that Plato, in his “old age,” had come to believe in the Philolaic system, with its “central fire.” Whether Plutarch’s statement accurately represents Plato’s later ideas is extremely doubtful. Nevertheless, the universal popularity of Plutarch’s Lives in the sixteenth century made this passage the most widely known description of Plato’s cosmological theories, and gave additional authority to the belief that he was a supporter of the Pythagorean system, and hence, by virtue of the prevailing misconception of that system, one who was in favor of the heliocentric hypothesis.
Plato, as we have observed, was well aware that none of the cosmological systems prevailing in his time accounted fully for certain conspicuous irregularities in the motions of the planets. One of these irregularities was the movement of the planets in latitude. This, as we now know, is due to the inclination of [37] the planetary orbits to the plane of the ecliptic, which causes these wandering stars to be seen sometimes north, and sometimes south, of the ecliptic circle. A far more difficult problem, however, was that of the retrograde motions of the planets. Eudoxus (circa 408-355 B.C.), a younger contemporary of Plato, took upon himself the task of working out a mathematical system of the planetary movements which would successfully solve these problems. The system he evolved consisted of twenty-seven homocentric spheres, whose centers were the center of the earth. One sphere was assigned to the fixed stars, three each to the sun and moon, and four each to the five planets. Of the four spheres assigned to a planet, the first and outermost rotated in twenty-four hours about an axis passing through the celestial poles, and had for its function the representation of the apparent daily motion of the entire heavens. The planet itself was pictured as attached to the equator of the innermost sphere, and the axis of each sphere had its poles attached to certain points in the sphere immediately inclosing it. By assigning the proper inclinations to these axes, and the proper periods of rotation to each of the globes, Eudoxus sought to make the combined movements of his various spheres produce in the planet a series of motions exactly corresponding to actual observations.
Eudoxus, so far as we know, was the first to work out a complete mathematical system of the universe taking into account the retrograde movements of the planets. His theory deserves genuine admiration, in spite of its defects. For Saturn, Jupiter, and Mercury, his system was entirely adequate to the task of accounting for the inequalities which, up to that time, had been observed in their motions. He was not so successful, however, with Mars and Venus. Moreover, there was one assumption inherent in his theory for all the five planets—namely, that they were always at the same distance from the earth. The variable brightness of the planets was difficult to explain under such a hypothesis.
Calippus, the immediate successor of Eudoxus, did not attack this latter difficulty, but he greatly improved Eudoxus’ [38] theoric for Mars and Venus by introducing a fifth sphere, and perfected that for Mercury by the same device. He also added two extra spheres apiece for the sun and the moon, to account for the unequal speeds of those bodies in their orbits—a fact which had been discovered about one hundred years earlier by Meton and Euctemon, but had not been taken into consideration by Eudoxus. Calippus’ system, therefore, contained thirty-three planetary spheres, plus the sphere of the fixed stars. In his work, and that of his master, we have the earliest recorded instance in which a mathematical theory was worked out, then compared in detail with observations, and subsequently modified to bring it into closer agreement with those observations.
We now come to Aristotle, and, because of his great influence for over two thousand years, we must consider his cosmological doctrines in some detail. His system was very largely eclectic. He adopted the ideas of certain of his predecessors and gave them the stamp of his great authority, so that they continued to pass current for many centuries. The beliefs of others of the earlier philosophers, however, were mentioned in his works only to be violently refuted, so that they had little chance of being revived successfully so long as Aristotle retained his supreme reputation for infallibility.
First of all, Aristotle accepted the mathematical system of homocentric spheres of Eudoxus and Calippus, well realizing that this was the most advanced attempt to represent geometrically the complex motions of the planets.[34] He was not content, however, to regard this system merely as a mathematical device for portraying and calculating the planetary movements. He definitely conceived the spheres as solid, material bodies, to which the planets were rigidly attached.[35] To explain the motions, he assumed that the outermost sphere of fixed stars, [39] as it rotated at the tremendous speed necessary to complete one circuit every twenty-four hours, affected the movements of all the planetary spheres it inclosed. These latter spheres, which, through their own proper motion, were traveling in the opposite direction, were nevertheless dragged along by the superior force of the sphere of fixed stars, which, according to Aristotle, was the first mover, or primum mobile. The planet closest to this stellar sphere consequently had the greatest difficulty in overcoming its force, and therefore required the longest time to complete its own revolution in the contrary direction. The moon, on the other hand, being nearest the earth and farthest from the primum mobile, took the least time to accomplish its circuit of the heavens.[36] Aristotle thus followed Plato in placing the planets in an order corresponding to their sidereal periods of revolution.
The system of homocentric spheres of Eudoxus and Calippus, valuable as Aristotle perceived it to be from the mathematical point of view, seemed to him to present a difficulty when he sought to combine it with his own physical theory that each sphere transmitted the greater part of its own motion to the next one inclosed within it. To overcome this difficulty, he introduced twenty-two additional spheres to counteract the varied motions produced by the spheres of Eudoxus and Calippus. Accordingly, between the set of spheres assigned to a certain planet and the set belonging to the planet immediately below it, Aristotle placed a number of “unrolling spheres,” the total in each instance being one less than the number used by Calippus in representing the motion of the upper planet. To each of these inserted spheres Aristotle assigned a motion of rotation about the same axis as one of the regular planetary spheres, but with an equal speed in the opposite direction. Thus, as he thought, he neutralized the movement of every sphere of that particular planet except its first, or outermost, sphere, which represented the diurnal motion of the stars. This left only the movement of the sphere of fixed stars to be [40] passed on to the first sphere of the planet immediately below. In all, Aristotle’s system involved fifty-five homocentric spheres.
Inasmuch as Aristotle had accepted the idea of the geocentric universe, he naturally rejected the older system of Philolaus. As an argument against it, he points out[37] that, if the earth revolved about a “central fire,” apparent changes in the relative positions of the fixed stars ought to be perceptible. Since this is not the case, and since, at any given latitude on the earth, the stars always rise and set in the same locations, he concludes that the earth must be in the center, and motionless. He does not seem to have known of Heraclides’ idea of the earth’s rotation about its own axis, whose poles coincided with the poles of the celestial sphere. At least, he failed to understand that this theory was intended to account for, and to replace, the motion of the fixed stars, and that it actually represented the observed facts just as accurately as the hypothesis of the earth’s immobility.[38]
Had Aristotle fully realized the importance and the implications of Heraclides’ proposal, he would have been forced to devote considerable space to its refutation. Most of the mathematical demonstrations offered in the first book of the De Caelo to prove that the universe was finite became automatically invalidated the moment the possibility of the earth’s rotation about its own axis was admitted as an alternative hypothesis to the theory of the earth’s stability. These proofs had been based upon the assumption that the heavens actually rotated about a motionless earth, and were designed to show that the infinite cannot be traversed in the finite time of twenty-four hours. Obviously, if one pictured the earth as the moving body, and the fixed stars as motionless, Aristotle’s proofs could not be applied.
One of the most striking features of the De Caelo is Aristotle’s evident concern over the ideas of Democritus and the atomistic school of philosophers, and his eagerness to demolish their doctrines, especially their assertion that there was an infinite [41] number of worlds and their theory of the atomic constitution of matter. Almost the whole of Book I of the De Caelo is given over to proving that, contrary to the ideas of the atomists, the universe was finite, whereas Book III is largely devoted to a refutation of atomism. Whereas Plato had been inclined to treat the doctrines of the atomists sympathetically, and even to accept some of their ideas, Aristotle was steadfastly opposed to their entire scientific philosophy. Consequently, the finiteness of the universe became a fundamental principle in the latter’s cosmology. Aristotle portrayed a tiny, motionless, spherical earth, located in the center of the universe, surrounded by the various planetary spheres, and definitely bounded by the sphere of the fixed stars, beyond which nothing whatever existed. He would not even admit the outer fire, or the infinite air beyond the stars, which was a part of the Philolaic system. He explicitly states: “There is therefore no infinite body beyond the heaven. Nor again is there anything of limited extent beyond it. And so beyond the heaven there is no body at all.”[39] In a later passage, he argues:
It is therefore evident that there is also no place or void or time outside the heaven. For in every place body can be present; and void is said to be that in which the presence of body, though not actual, is possible; and time is the number of movement. But in the absence of natural body there is no movement, and outside the heaven, as we have shown, body neither exists nor can come to exist. It is clear then that there is neither place, nor void, nor time, outside the heaven. Hence whatever is there, is of such a nature as not to occupy any place, nor does time age it . . .[40]
This finite universe, according to Aristotle, was eternal; it had had no beginning, and could never be destroyed.[41] The latter idea was again directly opposed to the atomists’ belief that worlds from time to time collided and were thus destroyed. On this point, at least, the atomists were in better accord with the later Christian doctrines of the creation of the world, and its coming destruction at the time of the Last Judgment. From the time of the revival of Aristotle’s scientific [42] works in the late Middle Ages, his assertion that the world was eternal, without beginning or end, was felt to be inadmissible and contrary to Christian beliefs, and was the only feature of his cosmology to be universally rejected by the Christian philosophers. Indeed, his doctrine of the eternity of the world was the main ground for nearly all the religious attacks on Aristotle’s natural philosophy in the sixteenth and seventeenth centuries.
On a priori grounds, Aristotle was convinced of the spherical shape of the earth, and of the universe itself, because of his metaphysical belief that the circle and the sphere were the most perfect figures. Nevertheless, he proceeds to offer very sound proofs of the earth’s sphericity. He notes, for example, that the earth’s shadow during an eclipse of the moon has a circular outline.[42] As the most cogent evidence supporting his hypothesis, he quite rightly brings forward the fact that the meridian altitudes of the fixed stars vary in direct proportion to the latitude of the observer, and, incidentally, mentions that this phenomenon also proves that the earth is comparatively insignificant in size. Because so many people today have the mistaken notion that the belief in the insignificant size of the earth dates from Copernicus, Aristotle’s statements on this question deserve special attention:
Again, our observations of the stars make it evident, not only that the earth is circular, but also that it is a circle of no great size. For quite a small change of position to south or north causes a manifest alteration of the horizon. There is much change, I mean, in the stars which are overhead, and the stars seen are different, as one moves northward or southward. Indeed there are some stars seen in Egypt and in the neighbourhood of Cyprus which are not seen in the northerly regions; and stars, which in the north are never beyond the range of observation, in those regions rise and set. All of which goes to show not only that the earth is circular in shape, but also that it is a sphere of no great size: for otherwise the effect of so slight a change of place would not be so quickly apparent. Hence one should not be too sure of the incredibility of the view of those who conceive that there is continuity between the parts about the pillars of Hercules and the parts about India, and that in this way the ocean is one. As further evidence [43] in favour of this they quote the case of elephants, a species occurring in each of these extreme regions, suggesting that the common characteristic of these extremes is explained by their continuity. Also, those mathematicians who try to calculate the size of the earth’s circumference arrive at the figure 400,000 stades. This indicates not only that the earth’s mass is spherical in shape, but also that as compared with the stars it is not of great size.[43]
Discussion up to this point has been confined to those broader aspects of the Aristotelian cosmology which have to do with the size of the universe, and the order and movements of the planets. Something must now be said of Aristotle’s physical theories, which were intimately connected with his astronomical system. The fundamental principle upon which his physics is based is a distinction between natural motion, and unnatural, or constrained, motion. Certain bodies, such as the four elements and the stars, are asserted to possess a principle of movement in their own nature, and are therefore termed simple bodies.[44] All others are compound bodies, and their movements are determined by the simple body which prevails in their composition. Each simple body has one, and only one, simple motion which is natural to it. Any other movement it undergoes is the result of some external force, and cannot be perpetual, since this external force cannot be perpetually applied. Aristotle recognized two types of simple motion, the rectilinear and the circular. The four elements—earth, water, air, and fire—are simple bodies, having natural motions in a straight line, either downward toward the center of the universe, as earth and water, or upward from the center, as air and fire. Each of these elements is thus paired with its opposite, which has a natural motion in a direction contrary to its own. Therefore, the region of the elements must [44] be subject to constant change or decay, for those alterations are produced by the conflict of contraries. But there must be another simple body whose natural motion is circular, and since, according to Aristotle, this type of movement has no contrary, it is essentially nobler, and the simple body to which circular motion is natural will not be subject to change but will be eternal. He therefore concludes that the simple body to which circular motion is natural is to be identified with the fifth element, of which the heavenly bodies are composed, since these bodies move in circles and are unchanging. He declares:
The mere evidence of the senses is enough to convince us of this, at least with human certainty. For in the whole range of time past, so far as our inherited records reach, no change appears to have taken place either in the whole scheme of the outermost heaven or in any of its proper parts. The common name, too, which has been handed down from our distant ancestors even to our own day, seems to show that they conceived of it in the fashion which we have been expressing. The same ideas, one must believe, recur in men’s minds not once or twice but again and again. And so, implying that the primary body is something else beyond earth, fire, air, and water, they gave the highest place a name of its own, aither, derived from the fact that it ‘runs always’ for an eternity of time.[45]
We see, therefore, that Aristotle gave his sanction to certain cosmological ideas connected with the doctrines of the four elements and the nature of motion and change which had already been suggested by Plato and other earlier philosophers. By combining these various theories into a logical and coherent system, he made them an essential part of almost every physical theory of the universe proposed during the next two thousand years. His fundamental distinction between the sublunary regions, the realm of the four elements where all was subject to change and decay, and the eternal, changeless, ethereal region, beginning with the moon and extending upward to the primum mobile, persisted well into the Renaissance. According to this theory, the ether was a fifth element, the constituent of the heavenly bodies and the vast spaces [45] through which they moved in circular paths. The space inclosed by the moon’s sphere was portrayed as filled by the four concentric spheres of the elements. The solid earth was in the center, and was necessarily globular in form, because all heavy things were seeking the center of the universe, which was located at the center of our terrestrial globe. In fact, our earth was originally formed by the process of the heaviest element seeking this center. The watery sphere encompassed that of the earth, but the boundaries between the two were irregular, because the higher parts of the land projected above the oceans which surrounded our globe. The sphere of air came next, and above it, but below the moon, was the fiery sphere, for fire possessed more of the spirit of “levity” in its nature, and hence tended to rise above the air. All unusual and transitory celestial phenomena, such as meteors and comets, were thought to take place either in the air, or in the fiery sphere just below the moon. They could not be pictured above the moon in the Aristotelian cosmology, because that region was considered eternal and unchanging.[46]
In Aristotle, therefore, we find almost every detail of the pre-Copernican cosmology set forth and supported by arguments which, if one grants his often fallacious basic assumptions, are most logical and convincing. The animistic strain of Plato, which led to the peopling of the spheres with a hierarchy of celestial spirits, is missing, but that was an excrescence which could readily be supplied by those who felt it desirable. The Aristotelian universe was inclosed in the finite spherical shell of the orb of fixed stars. At the center of this shell, scarcely more than a speck in comparison with the whole, was our earth, surrounded by the spheres of the other elements, and the orbs of the moon, sun, and the five planets. For the purpose of mathematical calculation and representation of the intricate movements of the planets, each of these wandering stars might be pictured with a group of several spheres appertaining to it (the sum of the spheres of Exodus and Calippus [46] and the “unrolling” ones added by Aristotle). The popular discussions, however, following Aristotle’s example in the De Caelo, passed over these complex mathematical details, and portrayed only a single sphere for each planet. This practice eventually gave rise to much confusion, for whereas the mathematical system of representing the planetary motions necessarily changed from time to time, in order to bring itself into agreement with the newly observed facts, the popular accounts of the structure of the universe often remained unchanged. Consequently, Aristotle’s cosmology, with its system of homocentric spheres, maintained its supremacy, even to the extent of causing the more advanced epicyclic theory to provide itself quite unnecessarily with the trappings of material spheres, in order to bring it into closer accord with the outgrown hypothesis of the great Greek philosopher.

Schema huius præmissæ diuisionis Sphærarum.
Fig. I.—Typical Pre-Copernican Diagram of the Universe
From the 1539 edition of Peter Apian’s Cosmographia
From the point of view of Renaissance thought, Ptolemy, with his mathematical system of eccentric circles and epicycles, made the most important modification of the Aristotelian cosmology before Copernicus. His work, while profoundly affecting the theories upon which the geometrical representation and calculation of the heavenly motions were based, influenced but slightly the underlying physical ideas of most students of astronomy. The precise nature of Ptolemy’s contribution to astronomy may be better understood if we first sketch briefly the progress of that science during the four and one-half centuries intervening between Aristotle’s day and his own, keeping in mind the outline of the elementary facts of the planetary motions which was given earlier in this chapter.
The system of homocentric spheres received no further development after Aristotle. The reason was obvious, and was clearly stated by certain ancient writers on the history of astronomy, notably by Simplicius in his commentary on the De Caelo.[47] The great variation in the brightness of the planets when at different points in their orbits, particularly noticeable in the cases of Venus and Mars, made the idea of uniform [48] distance from the earth untenable. Moreover, it was noted that the disk of the moon varied almost ten per cent in diameter during the course of a month. Consequently, the astronomers and mathematicians sought to work out a new system, which should represent satisfactorily the changing distances of the planets. The progress of astronomy was greatly furthered during this same period by the establishment of the Museum at Alexandria, where a school of observers arose who determined the position of the stars by means of graduated instruments, and kept a record of their findings over several centuries. The resulting increase in the quantity of accurate astronomical data proved of inestimable value to the mathematicians in checking their calculations.
The system gradually developed during these centuries, which received its final synthesis and expression in Ptolemy’s Mathematical Syntaxis,[48] portrayed the movements of the planets by means of eccentric circles and epicycles. First, apparently, the theory of movable eccentrics was worked out. The centers of the planetary orbits were placed, not in the earth, but on a straight line joining the earth and the sun. Thus, as the sun proceeded on its apparent course about the earth, this line of the centers swept over a circle whose center was the earth, and the center of each planetary orbit described a circle about the earth in the course of a year. The system of movable eccentrics would work only for the superior planets, Saturn, Jupiter, and Mars. For the inferior planets the epicyclic theory had to be substituted. In this system the planet moved on the circumference of a small circle, the epicycle, whose center lay on the circumference of another circle, the deferent, which was concentric with the earth. The center of the epicycle moved around the deferent in a period of one year, in the case of the inferior planets; meanwhile, the planet was moving around [49] the circumference of the epicycle in a period corresponding to the cycle of its progressive and retrograde motions, or, in terms of modern astronomical theory, its period of revolution about the sun.
Once the epicyclic theory was developed, the geometricians soon discovered that it could represent the motions of the superior planets just as well as the method of movable eccentrics, and had the advantage of more clearly illustrating the stationary points and retrograde motions of the planets. It was only necessary to make the period of the center of the epicycle about the deferent equal to the sidereal period of the superior planet, and the planet’s own period in its epicycle equal to one year. A consideration of the geometrical properties involved in this simple epicyclic system will clearly reveal its ability to solve satisfactorily a number of troublesome problems connected with the planetary motions. First of all, it could account for the variable distances of the planets, because at one point of its orbit the planet would be at a distance from the earth corresponding to the sum of the radii of the deferent and the epicycle, while at another point its distance would equal the difference of those radii. Furthermore, by a proper selection of the ratios between the radii of deferent and epicycle, the retrograde arcs of the planets could be represented in accordance with the observed facts, for the apparent direction and velocity of a planet would be the resultant of the combined motions of the epicycle and deferent. The variations in the latitudes of the planets could likewise be well accounted for by the expedient of giving the plane of the epicycle the required inclination to the plane of the ecliptic, which coincided with the plane of the deferent.[49]
The simple epicyclic system was used by Hipparchus (fl. 140-129 B.C.), Ptolemy’s famous predecessor.[50] But even in Hipparchus’ time the known inequalities in the orbital velocities of the sun, moon, and planets had become so complex that he suggested that in the future it would be necessary to combine the epicyclic theory with the movable eccentrics by using eccentric circles for deferents.
The combination of the epicyclic and eccentric systems received its final development at the hands of Ptolemy (fl. 127-150 A.D.). In the Almagest the motions of the sun, moon, and planets are all worked out geometrically by the use of these eccentric deferents and epicycles. Ptolemy also introduced an added refinement, necessary in order to make theory and observation agree, by having the center of the epicycle move around the deferent with an angular velocity which was uniform, not with respect to the center of the deferent, but with respect to another point, the equant. This point was so located that it was the same distance from the center of the deferent as the latter was from the center of the earth, but on the opposite side, so that the center of the deferent was midway between the equant and the earth. By this device the changing velocity of [51] the sun, moon, and planets in their orbits was more accurately represented.
There is no need to go more deeply into the complex mathematics of Ptolemy’s great work. It is essential, however, to emphasize the fact that he regarded his system primarily as a set of mathematical constructions designed in order to calculate accurately the positions of the planets.[51] At the beginning of his Hypotheses of the Planets[52] he says that this work is a précis of his Almagest, and declares that he does not pretend to give the reasons for all the planetary movements, but merely to make clear his system for representing geometrically the observed motions. This same attitude had been maintained throughout his greater work.
In common with his contemporaries, Ptolemy accepted the physical theories of Aristotle: the central position of the earth, and the doctrine of the four elements, each with its own sphere in the sublunary region. Like Aristotle, he thought of the starry sphere as rotating about a motionless earth; but, in order to account for the precession of the equinoxes, he was forced to assume a ninth sphere, above the fixed stars. This ninth sphere became the primum mobile, turning about once every twenty-four hours, whereas the eighth sphere, holding the fixed stars, was now given a movement of its own of about one degree in one hundred years, in a direction opposite to that of the first mover.[53] Ptolemy, however, attempted no mechanical explanation of the movements of the planets. Instead, he sought merely to discover the “how” of these phenomena, leaving the “why” to others, and was content with [52] a mathematical system which, to use the term so common in the Renaissance, would “save the phenomena.”
Ptolemy gave his sanction to a change in the Aristotelian order of the planets that had been introduced some two centuries earlier by the Stoic school of philosophers. The Stoics placed the sun in the middle of the seven planets, so that three were above it (Saturn, Jupiter, and Mars) and three below it (Venus, Mercury, and the moon). Although this order had prevailed among the Babylonians from early times, the Stoics were the first to adopt it and give it currency in the Mediterranean world, and they did so because it happened to fall in with their notion that the sun was the ruling power in the universe. Ptolemy accepted this order as the most probable, but remarked that there was no means of settling the question, because none of the planets had a sensible parallax and hence there was no way of measuring their actual distances from the earth.[54] He nevertheless concluded that one might reasonably suppose that the sun was between the planets that never wandered far from it, and those that wandered at will.
Ptolemy’s mathematical system of the universe deserves our whole-hearted respect. He attacked the problems he had set for himself in a thoroughly scientific manner, and sought only to devise a method whereby all the complexities of the planetary motions might be portrayed and calculated. He did not allow himself to be diverted by any preconceived metaphysical notions as to first causes, nor seek to simplify his task by ignoring any of the observed facts. The great proof of the excellence of his achievement is that his system did in truth represent the motions of the heavenly bodies with a fidelity to the observational data fully equal to the accuracy of those data [53] in his own time. Moreover, as additional variations were discovered, they could readily be made a part of his mathematical theory by a further application of his methods. It is therefore no wonder that his system remained the foundation of scientific astronomy for fourteen centuries, easily surviving all attempts to supplant it by hypotheses which proved, on close examination, to have evaded the problem of accounting for the more troublesome facts of the movements of the stars.
Ptolemy’s successors, however, were not content with a theory that was merely mathematical, and began immediately to inject additional assumptions into the body of his scheme. First, they sought to give physical reality to his deferent and epicyclic circles by picturing them as the equators of material spheres. His epicycles, for example, were portrayed as small, solid, crystalline spheres, moving within the annular space between two other solid spheres eccentric to the earth. The planet itself was attached to the equator of the epicyclic sphere. In this fashion all of Ptolemy’s mathematical constructions were given material form, and the resulting system approximated the solid, crystalline spheres of Aristotle’s cosmology. These spheres, however, were no longer homocentric, and the celestial mechanics involved in the conception was no longer simple, but infinitely and incredibly complex.
Some sanction was given to this attempt to combine the Aristotelian and the Ptolemaic astronomy by a work attributed to Ptolemy himself. This work purports to be the second book of the Hypotheses of the Planets, and has been preserved only in an Arabic translation, although copies of the first book of the Hypotheses have survived in the Greek original. The Arabs, to whom we owe the preservation of the writings of Ptolemy and the other Greek scientists during the period when European science had sunk to the low level of the Middle Ages, all adopted this Aristotelian idea of solid spheres. They made the conception an integral part of the Ptolemaic astronomy, and so passed it on to the western world. Because of the second book of the Hypotheses, which they attributed to Ptolemy, they had apparent authority for this [54] action, but the ruling motive was doubtless the earnest desire to reconcile the two systems.
The ancients introduced two additional foreign elements into Ptolemy’s cosmology, in both instances without any authority whatsoever in his own writings. The first was the idea that the distances of the planets from the earth were accurately known. The epicyclic system could give no clue whatever to the actual distances of the planets. It could only give the ratio, for each planet, of the radii of deferent and epicycle, which was calculated from the observed length of the retrograde arc. Later writers were unwilling to be left in the dark concerning the dimensions of the planetary orbits, and Proclus (410-485 A.D.), one of the last of the important writers on astronomy in the ancient world, tells us that by his time some people, supposing the actual distance of the sun and moon to be known,[55] assumed that there was no vacant space in the universe, and filled all the intervals with the various planetary spheres. The greatest distance of the moon (64-1/6 earth radii) was assumed to equal the least distance of Mercury, while the greatest distance of Mercury was equal to the least distance of Venus, and so on, out to the sphere of the fixed stars. The Arabs adopted the notion, worked out the dimensions of the spheres according to this hypothesis, and incorporated the results of their calculations in the system of Ptolemaic astronomy which they passed on to Europe in the twelfth century.
The second idea imposed upon the astronomy of Ptolemy was that the precession of the equinoxes was not uniformly progressive in one direction, but oscillated backwards and forwards through an arc of eight degrees. When, at a later date, Arabian observers found that Ptolemy’s figure for the rate of precession was too small, this oscillatory motion was combined with the theory of uniform precession, and the idea of variable precession, or trepidation, obtained a foothold among [55] astronomers. To represent this imaginary phenomenon of trepidation, the Arabs added a tenth sphere to the system. This extra sphere now became the primum mobile, the ninth sphere accounted for the progressive motion of the equinoxes around the heavens, while the sphere of the fixed stars had its poles moving about small circles located on the surface of the ninth sphere, thereby producing the supposed periodic inequality of precession. This theory received its final development in the Alfonsine tables, completed in 1252 by Alfonso X of Castile and a group of astronomers working under him. According to these tables, the equinoxes moved around the heavens in 49,000 years, while the period of the trepidation was 7,000 years.
We have already observed how Greek astronomy was kept alive and developed by the Arabs during the Middle Ages, and have noted some of the changes they incorporated in the Ptolemaic system. Among the western nations astronomy was almost nonexistent as a science from the sixth until the twelfth century, and the original works of Ptolemy, Aristotle, and the other Greek scientists were unknown. Such knowledge as men had of the ideas of these ancient writers was gleaned at second hand, from references in the works of the early leaders of the Christian church, or in the Latin encyclopedias that happened to be preserved and read during those centuries. The most important of these encyclopedic works were Pliny’s Natural History, Chalcidius’ commentary on Plato’s Timaeus, Macrobius’ commentary on Cicero’s Somnium Scipionis, and Martianus Capella’s De nuptiis Philologiae et Mercurii et de septem artibus liberalibus. Almost all of the detailed astronomical information found in most medieval writings is traceable to one of these four sources. Because the last three of them mentioned the theory of Heraclides which made Venus and Mercury revolve about the sun, we find many references to this idea in the Middle Ages, but in most cases the medieval author in question clearly lacked the general astronomical knowledge to understand what was really meant by this hypothesis.[56]
In addition to these encyclopedias of ancient science, a second significant influence on the astronomical thought of the Middle Ages is to be found in the writings of the early Fathers of the Church. Some of these Christian theologians, notably Lactantius, bitterly attacked all scientific learning, taught that the earth was flat, and, in general, reverted to the most primitive ideas of the nature of the universe, backing up their contentions by quotations from the Scriptures. Churchmen of Lactantius’ sort need not seriously concern us, however, for by the time of the Renaissance even the Church no longer defended their ignorant bigotry. An entirely different group of early Church Fathers included such figures as Clement of Alexandria, Origen, Basil, and Augustine. These men all had some familiarity with Greek philosophy, particularly with that of the neo-Platonic school, and were sympathetic towards the ideas of Greek science, whose findings they sought to incorporate in their theology wherever they did not conflict with fundamental Christian dogmas. Moreover, most of the early Christian theologians were, like the four just mentioned, profoundly influenced by the doctrines of Plotinus and the ancient neo-Platonists. Thus most of the mystical beliefs of the Church came to be permeated with neo-Platonism, and particularly with its idea of a hierarchy of spirits inhabiting the celestial spheres. Consequently, the picture of the heavens as consisting of eight spheres encircling the earth, and the conception of these spheres as the homes of the various orders of angels, gradually became one of the accepted tenets of Christianity. In this picture the abode of God was placed in an immovable region above the fixed stars—and also above the primum mobile, whenever the latter was portrayed as a distinct sphere, outside the firmament. To represent the dwelling place of God and the highest orders of angelic spirits, an extra sphere, the empyrean, was added to the old cosmology. This sphere shone perpetually with the purest and most brilliant light. Taken with the name “empyrean,” this quality clearly indicates that the ultimate source of the conception was probably the old Philolaic idea of the Olympus and the outer fire.
Finally, in the twelfth century, the science of astronomy began to be revived in Europe, chiefly through translations into Latin of the Arabic versions of the works of Ptolemy and Aristotle. At the same time Arabic treatises based upon these and other ancient scientific writings were also translated and became known in western Europe. Of the Arabian astronomical writers who in consequence acquired great influence and renown, the two most prominent were Al Fargani (fl. 861 A.D.), commonly known in Europe by the Latinized form of his name, Alfraganus, and Al Battani (circa 858-929), known as Albategnius. These Mohammedan astronomers had redetermined some of the astronomical constants given in Ptolemy, and had slightly modified a few of his figures to make them agree more closely with recent observations.[57] Both Alfraganus and Albategnius accepted the idea that the greatest distance of each planet from the earth was equal to the least distance of the planet next above it, and worked out tables of the stellar distances upon this basis.[58] Having thus, as they thought, accurately determined the distance of each planet, they proceeded, from measurements of the apparent planetary diameters, to compute their sizes. Alfraganus’ figures are worth recording, because they appear in most of the popular works on astronomy published during the Renaissance, and were accepted with only slight modifications by Copernicus. The Arab astronomer recorded the size of the moon as 1/39 of that of the earth, Mercury as 1/32,000, and Venus as 1/37 of the earth in volume. The sun was set down as 166 times [58] as large as the earth; Mars as 1-5/8 times, Jupiter as 95 times, and Saturn as 90 times. The smallest of the fixed stars were declared to be considerably larger than the earth.[59]
The works of Alfraganus were translated from Arabic into Latin in the twelfth century by John Hispalensis and Gerard of Cremona, and those of Albategnius by Robert of Chester and Plato of Tivoli.[60] During the same period the first translations of the Almagest were made. Gerard of Cremona translated Ptolemy’s work from Arabic into Latin about 1175, but a less-known translation from the Greek had been made in Sicily some fifteen years earlier.[61] At last the astronomical science of the ancient world, as summarized in the Almagest and the writings of the Moslem astronomers who had preserved this learning throughout the intervening centuries, was made available to the nations of western Europe.
Coinciding with this recovery of the mathematical astronomy of Ptolemy was the revival of interest in Aristotle’s scientific works. These were first translated from Arabic into Latin by Gerard of Cremona in the second half of the twelfth century.[62] During the Middle Ages, only those works of Aristotle dealing with dialectics had been known in Europe. The impetus for the revival of the study of Aristotelian science came originally from Spain. There, during the twelfth century, a school of Moslem philosophers arose which enthusiastically accepted Aristotle as the infallible master of all scientific knowledge, and spread his doctrines to the Christian world. Averroës (1126-1196) was the most famous of these Mohammedan philosophers, while Ibn Tofeil (d. 1186) and [59] his pupil, Al Bitrugi, known in Europe as Alpetragius, were the most eminent astronomical writers. Because of their worship of Aristotle as a scientist, the acceptance of his system of homocentric spheres, or some modification of it, seemed a necessity to these Moslem scholars, and they consequently rejected the system of epicycles. Alpetragius was the author of a novel theory designed to revive the principle of the concentric spheres, although the original idea may have been due to his master, Ibn Tofeil.[63] He went back to the primitive notion that the first mover produced all the motions of the lower spheres, and rejected the independent movement of the planets from west to east. This, in itself, was definitely a backward step. But Alpetragius clearly saw that the simple, pre-Aristotelian theory was wholly inadequate unless some modifications were introduced. It was necessary to account, not only for the fact that the poles of the ecliptic differed from the celestial poles, but also for the motions of the planets in latitude, and their variable velocities in longitude. He endeavored to represent these motions by letting the poles of each planet’s orbit describe small circles around their mean positions (the poles of the ecliptic) in a period equal to the synodic period of the planet.[64] Because the “lagging” of Venus, in his theory, was smaller than that of the sun, Alpetragius altered the order of the planets, placing Venus between Mars and the sun.
Alpetragius never calculated all the details of his system mathematically, probably because of the difficulties he encountered in trying to make it account accurately for the observed retrograde arcs of the various planets. For this reason, it could be of little use to scientific astronomers, who saw in it the additional defect that it assumed a planet to be always at the same distance from the earth. This was the very objection that had caused the abandonment of the system of Eudoxus and Aristotle many centuries before. The great interest to us of the [60] theory of Alpetragius lies in the evidence it gives of the earnest desire of the Spanish Aristotelians to overcome the difficulties of reconciling the Ptolemaic system with the physical theories of Aristotle, and their conviction that the hypotheses set forth in the Almagest were no more than convenient schemes for computing the stellar motions and had nothing to do with the physical realities.
The treatise of Alpetragius, written about 1190, was translated from Arabic into Latin in 1217 by Michael Scot, who also translated Averroës’ commentaries on the scientific works of Aristotle.[65] Well before the middle of the thirteenth century, therefore, both Aristotelian science and Ptolemaic astronomy, as handed down by the Arabs, became the property of the Schoolmen. The introduction of these works at the universities of Paris and Oxford brought about a prolonged strife between the Aristotelian and the Ptolemaic systems of the world. By the middle of the thirteenth century Aristotelian natural philosophy had become firmly established at the Scholastic seats of learning. The two most eminent Schoolmen, Albertus Magnus (1193-1280) and his disciple, Thomas Aquinas (1227-1274), devoted their energies to working out a synthesis of Aristotelian science and Christian theology. Both men at first were inclined to adopt the system of Alpetragius, and Albertus even went so far as to simplify it to the extent of making it quite useless. But these Scholastic writers, as they went deeper into the study of astronomy, gradually abandoned Aristotle for Ptolemy. Thomas Aquinas wrote an able commentary on Aristotle’s De Caelo, in which he pointed out the reasons why later astronomers, and particularly Ptolemy, had been forced to modify the system of homocentric spheres.[66] He clearly perceived a fact which had been brought home inexorably to every thorough student of astronomy—namely, that it was easy enough to work out some fairly simple and apparently logical theory of the universe, so long as one was content to represent only a few of the principal phenomena [61] and ignore the others. The complexity, and likewise the superiority, of the Ptolemaic system was due to its taking into full account every known detail of irregular motion.
Through the influence of their most noted leaders, the Schoolmen’s astronomical doctrines came to be based upon Aristotle, but combined his physical theories with the mathematics of Ptolemy in much the same way as the later Greeks and the Arabs had done. Hence, they either regarded the constructions of the Almagest as purely theoretical, or, more generally, gave them material existence as solid, crystalline spheres. The elementary textbook of astronomy written by Joannes de Sacrobosco (d. 1256) therefore accorded perfectly with the ideas of the Scholastic philosophers, although it was merely an epitome of the works of Alfraganus and Albategnius.[67] The commentaries by other writers, which frequently accompany both the manuscripts and the printed editions of Sacrobosco’s Sphaera mundi, usually supplement his descriptions by more detailed information gathered from the works of the same Moslem writers. It is therefore easy enough to understand why Sacrobosco’s treatise became the most popular astronomical textbook and was regularly used in the Schools.
The synthesis of astronomical theories made by the Schoolmen, however, brought with it the germs of its own destruction. Scholasticism accustomed men to examine the various cosmological ideas in the light of reason. At the same time, in the works of Aristotle which they were eagerly studying, they found numerous references to other hypotheses concerning the construction of the universe. Thus, independent and inquiring minds began to ponder upon the arguments that might be offered in favor of the systems which Aristotle had rejected. Meanwhile, as more and more of the ancient writings containing references to Greek astronomical speculations were recovered and made available to scholars, the information relating to these earlier cosmological theories rapidly increased. Seneca’s Naturales Quaestiones, which contained references [62] to the idea of the earth’s rotation,[68] became known in the twelfth century, about the same time as Aristotle’s scientific works.[69] In 1266 Simplicius’ commentary on Aristotle’s De Caelo was translated from Greek into Latin by William of Moerbeke,[70] and was used by Thomas Aquinas in his own treatise on the heavens.
During the fourteenth and fifteenth centuries European scholars continued their efforts to discover and make available additional literary and scientific works of ancient Greece and Rome. Translations from Greek writings multiplied, and the knowledge and appreciation of the ideas of the early Greek philosophers advanced with each succeeding decade. Plato, quite naturally, held the chief place among these philosophers, and as the humanists became better acquainted with his works a strong and most influential neo-Platonic school grew up, which reached its full flowering in the famous Platonic Academy of Florence in the fifteenth century. Marsilio Ficino (1433-1499), who completed a translation of Plato into Latin in 1477,[71] and Giovanni Pico della Mirandola (1463-1494) were the most famous members of this academy. These neo-Platonists set Plato up as a greater philosopher than Aristotle, and endeavored to work out a synthesis of his ideas with Christian theology. The Pythagorean number mysticism, a strong belief in the value of mathematics, and a conviction that the universe was made up of geometrical units arranged according to principles of mathematical harmony, were among the fundamental characteristics of the neo-Platonic philosophy, which received its best-known expression in the writings of Pico della Mirandola. In this school, too, we find another revival of the animism of Plato with its peopling of the universe with a hierarchy of spirits which, in agreement with Christian theology, were imagined as angels of various ranks. The fifteenth-century neo-Platonists also gave their support to the idea of an infinite realm beyond the finite sphere of the primum [63] mobile, pictured as the home of God and the highest order of spirits and the region of purest ether.[72]
As we have already noted in the first chapter, the mathematical, Pythagorean elements in this neo-Platonic philosophy were opposed to the prevailing tendency of Aristotelianism to minimize the importance of mathematics in the interpretation of the material world. Thus it was the neo-Platonists who gave the philosophical sanction and impetus to the new scientific investigations of physical phenomena. Their first function, however, was to call into question the settled ideas of the supporters of Aristotle, and to push forward Plato and the pre-Socratic philosophers as opposing authorities. Consequently, at the beginning of the sixteenth century, the problems of cosmology were very real and vital subjects of philosophical dispute, and the clash of conflicting ideas was evident in almost all serious, up-to-date works on astronomy.
It was this state of warfare between rival theories that prompted men to make earnest efforts to ascertain the true words and meaning of the ancient texts. No longer content with Latin translations of Arabic paraphrases, scholars sought out the Greek originals and rendered them into Latin. Georg Peurbach (1423-1469), one of the ablest astronomers of the time, was led by his desire to become better acquainted with the true text of the Almagest to seek for a Greek copy of that work through the aid of Cardinal Bessarion. Peurbach was a keen student of Ptolemy, and wrote an excellent textbook entitled Theoricae novae planetarum, in which he described the latter’s constructions, but adopted the Arabic idea of solid, crystalline spheres. Unfortunately, Peurbach died before he achieved his aim of making a thorough study of the Greek text of the Almagest, but his work was completed by his distinguished pupil, Regiomontanus (1436-1476), whose book, Epitome [64] in Ptolemaei Almagestum, was first printed at Venice in 1496.
The printing press contributed greatly to the spreading of conflicting astronomical ideas throughout Europe. By 1543, the date of the publication of Copernicus’ De revolutionibus, every important work on ancient astronomy was available to scholars in printed editions, except for the writings of Archimedes (famous for their detailed references to the system of Aristarchus of Samos), which were first published in the following year.[73]
Let us now summarize the situation as it existed on the eve of the appearance of De revolutionibus. The system of the world most generally accepted was almost wholly Aristotelian as far as physical theories were concerned. However, all scientists who had made any thorough study of astronomy had discovered that the system of homocentric spheres was entirely inadequate for the representation of all the facts of the motions of the heavens. Therefore, the Ptolemaic system of epicycles and eccentric circles had been merged with the Aristotelian cosmology, but, following the practice of the Arabian astronomers, the circles employed in the Almagest were usually transformed into a complex mechanism of solid spheres. Many Christian writers, attracted by the mystical elements in neo-Platonism, had added the Platonic idea that the spheres were inhabited by a hierarchy of spiritual beings. But by the fifteenth century the revival of knowledge concerning the speculations of Plato and the pre-Socratic philosophers had brought the problems of cosmology again to the fore, and the true scheme of the universe, instead of being a settled issue among scholars, was the subject of bitter dispute in which all the diverse theories gathered from ancient writers were being once more debated by the learned world. As yet, however, there was no mathematical system for calculating the planetary motions which could seriously rival that of Ptolemy. From the scientific point of view, therefore, the supporters of Ptolemy were justified in maintaining that his was the only system that could both fully and accurately represent the observed facts.
The pre-Copernican cosmological theories discussed in the preceding chapter were all familiar to scholarly Englishmen of the early sixteenth century. Many owned manuscripts of astronomical works, such as Latin translations of the Almagest, or of the works of the famous Arabian astronomers. Manuscript treatises based on these books were even more common, as were translations of Aristotle’s scientific works and the commentaries thereon by Simplicius and Averroës.[74]
Manuscripts, however, were costly, and only the wealthy could afford to own many of them. With the invention of printing, a far greater number of scholars found it possible to acquire libraries in which the important books dealing with astronomy were well represented. Although the early editions of these books were all the product of continental presses, numerous copies found their way to England and became available to English scholars.[75] This was also true of the astronomical works by foreign scholars of the fifteenth and sixteenth centuries. In this class belong the writings of Peurbach, Regiomontanus, Nicholas of Cusa, John Stöffler, Peter Apian, Gemma Frisius, and Oronce Finé.
There was a second class of astronomical books which, although written in Latin, had a far wider audience than the more advanced and learned treatises we have just discussed. These were the popular textbooks designed, not for the expert, [67] but for the average student interested in learning only the elementary facts of astronomy. The most famous of them was the Sphaera mundi, written in the middle of the thirteenth century by an Englishman, John of Hollywood, or Joannes de Sacrobosco, as he was commonly called. This little treatise sets forth the basic principles of the Aristotelio-Ptolemaic astronomy as handed down by the Arabs. The author draws his material principally from Alfraganus, and consistently follows the Moslem writer wherever he diverges from Ptolemy, so that he evidently had no first-hand knowledge of the Almagest. His book pictures the sublunary spheres of the elements and nine moving spheres in the usual order, with the primum mobile as the ninth sphere, above the firmament. It explains the rising and the setting of the stars, the diversity in length of days in different seasons and different parts of the world, the causes of eclipses, and many other matters of this sort. Only at the end does it mention that the planets move on epicycles, saying that this accounts for their retrograde motions. It makes no attempt to go into any of the complex details of these motions.
The Sphaera mundi, in short, did not include anything beyond the simplest and most obvious movements in the heavens. Because it failed to take up the more complex details of astronomy, it was often accompanied, both in the manuscripts and the early printed editions, either by commentaries or by additional treatises which aimed to carry the reader deeper into the subject of the planetary motions. The earliest printed edition I have seen, that printed in Venice in 1478 (Hain, No. 14108), is followed by Gerard of Cremona’s Theorica planetarum. More frequently, Peurbach’s Theoricae novae planetarum accompanies these early editions of Sacrobosco.[76] The commentaries on the Sphaera mundi most often found in the pre-Copernican editions are those by Cecco d’Ascoli (1257-1327) and Jacques Le Fèvre d’Étaples (circa 1455-1537), known as Jacobus Faber Stapulensis. Some idea of the great [68] popularity of Sacrobosco’s book may be gathered from the fact that no less than twenty-seven editions, either singly or with commentaries, are listed by Hain in his Repertorium Bibliographicum[77] as printed before 1501; and Copinger, in his supplement to Hain’s work, records three more editions.[78] By the middle of the seventeenth century, at least seventy Latin editions had been printed.[79]
An even more elementary work than Sacrobosco’s was Proclus’ Sphaera. It was first printed by Aldus Manutius in his Scriptores astronomici veteres in 1499; both the Greek text and a Latin translation by the Englishman, Thomas Linacre, were included in this volume. Linacre’s translation of Proclus was many times reprinted on the Continent, and was well known in England in the early sixteenth century.[80]
Other popular textbooks of astronomy were Gregory Reisch’s Margarita philosophica (Friburg, 1503) and Peter Apian’s Cosmographiae introductio (Ingolstadt, 1529-31). The astronomical section of the former work attempts to go deeper into the subject than Sacrobosco, but its material is essentially the same. In fact, what Reisch tries to do is to combine the matter of the Sphaera mundi, and the commentaries thereon, with Peurbach’s Theoricae novae planetarum, at the same time condensing the whole. Thus, especially in the later portions, his work suffers from the usual faults of unduly abbreviated discussions of highly complex questions. Apian’s Cosmographiae introductio, on the other hand, gives an even shorter exposition of the elements of astronomy than is found in Sacrobosco, and then proceeds to a presentation of what we would today class as geography.[81] Both his work and the Margarita philosophica were reprinted many times during the sixteenth century.
There were many other Latin works dealing with astronomy which were well known to Englishmen in the first four decades of the sixteenth century, but those mentioned were the most important and representative. One other book should be noted here, although, because it did not become generally known in England until after 1543, the discussion of its contents and influence will be reserved until a later chapter. The work in question is the Latin poem entitled Zodiacus vitae, written by Marcellus Palingenius. First published about 1531, it became one of the most popular Latin poems of the Renaissance, rivaling the eclogues of Mantuan in influence and renown. Its astronomical sections are of particular significance because Palingenius was thoroughly imbued with neo-Platonism, did not hesitate to criticize Aristotle, and mentioned in his verses many of the cosmological speculations of the pre-Socratic philosophers.
More important than these Latin works, so far as disseminating a knowledge of the elements of astronomy among all classes was concerned, were the books written in English. In 1543, however, no good astronomical text in English had yet been published. Therefore, those who could not read Latin were limited to the information set forth in those sections of the popular encyclopedias which dealt with cosmology. Among the earliest works printed by Caxton and his successors were translations of medieval works of an encyclopedic character, such as the De proprietatibus rerum of Bartholomaeus Anglicus or the Image du monde of an unknown French poet of the thirteenth century.
The first dated book printed by William Caxton in England, [70] The dictes or sayengis of the philosophhres (1477),[82] might seem, on first thought, to be a compendium of this sort, since Pythagoras, Plato, Aristotle, and Ptolemy are among the philosophers considered. However, it is nothing more than a compilation of moral maxims and proverbial sayings, made by a medieval author who had no knowledge of the works of any of the philosophers listed. The opening of the section on Ptolemy is a fair sample of the true nature of the book:
Tholom was a ryght wyseman and well vnderstanden & in especyall in foure scyencis yt is to wytte geometrye/ musike arysmetryke/ & astrologye/ and he made many good bokes amonge ye whiche one is called Almageste the whiche is of astrologye.[83]
Quite different in character from the Dictes was the Image du monde, translated from the French by Caxton himself and published in 1481 under the title of The Mirrour of the World. The original was a rhymed poem written in 1245, apparently by a certain Gossouin.[84] The author was thus a contemporary of Sacrobosco and drew upon the same sources for his astronomical knowledge. About half of the work is devoted to an exposition of the nature of the physical universe and the rest deals mainly with geography. The ideas set forth represent, on the whole, the best astronomical thought of the thirteenth century, and the author shows himself a thorough master of the general knowledge of his time. Although his method is purely descriptive, rather than mathematical and analytical, he succeeds in giving a clearly defined and unified picture of the entire system of the universe as it was conceived by the best-educated writers of the late Middle Ages and the early Renaissance. [71] Caxton’s translation, therefore, became the best and most thorough presentation in English of the science of astronomy, and remained so until after 1543. The Mirrour of the World contained far more actual astronomical data than Sacrobosco, although it did not, like the Sphaera mundi, present the mathematical proofs of the earth’s spherical shape and other matters of that sort. The twentieth chapter, entitled, “Of the meuynges of heuen and of the vii planetes, and of the lytilnes of therthe vnto the Regarde of heuen,” is a good illustration of the general character of the work:
Owr Lord God gaf meuyng vnto the heuen whiche goth so swyftly & so appertly that noman can comprise in his thought; but it semeth not to vs for his gretenes, nomore than it sholde seme to a man, yf he saw fro ferre an horse renne vpon a grete mountayne, it shold not seme to hym that he wente an only paas; and for somoche as he sholde be most ferre fro hym, somoche the lasse sholde he seme to goo. And the heuen is somoche hye and ferre aboue vs, that yf a stone were in thayer as hye as the sterres be, and were the most heuyest of alle the world, of leed or of metall, and began to falle fro an hye aboue, this thyng is proued and knowen, that it shold not come to therthe tyl thende of an hondred yere, so moche and ferre is the heauen fro vs, the whiche is so grete that alle the erthe round a boute hath nothyng of gretenes ayenst the heuē, nomore than hath the poynt or pricke in the myddle of the most grete compaas that may be, ne to the grettest cercle that may be made on therthe.
. . . . . . . . . .
Thus gooth and cometh the sonne the whiche neuer shal haue reste ne neuer shal fynysshe to goo wyth the heauen, lyke as the nayle that is fixed in the whele, the whiche torneth whan she torneth. But by cause that it hath meuyng ayenst the cours or tornyng of the firmament, we shal saye to yow another reson: Yf a flye wente rounde aboute a whele that wente rounde it self, and that the flye wente ayenst it, the whele shold brynge the flye with her. And so shold it falle that the whele shold haue made many tornes whilis that the flye shold make one torne, and er she had gon round aboute the whele vnto the first poynt. So ye muste vnderstonde that in suche manere goon the mone and the sonne by a way that is comune to the vii planetes that ben on the heuen, whiche alle goo by the same way, alleway to ward the eest. And the heuen torneth to ward the weste, lyke as nature ledeth hym.[85]
Compared with the straightforward, consistent cosmology given in The Mirrour of the World, the astronomical sections of the De proprietatibus rerum of Bartholomaeus Anglicus[86] present a hodgepodge of conflicting notions drawn from a variety of sources—Martianus Capella, Plato, Aristotle, and the early Church Fathers—with only a bare smattering of Ptolemy and his Arab commentators. As an introduction to the elements of astronomy it could only be extremely confusing, without giving the reader any clear idea of the fundamental conceptions of the science.[87]
The sixteenth-century Englishman found a much better exposition of cosmology than Bartholomew’s in that encyclopedic work, the Kalender of Shepherdes, a translation of the French book, Le Compost et Kalendrier des bergiers. The earliest known French edition of the work was published at Paris in 1493. It proved an extremely popular compilation of a great variety of lore. The concluding portion consists of an exposition of astronomy and astrology, with special emphasis on the latter. The book was translated three different times into English—in 1503, 1506, and 1508. Later editions were based upon the last and best of these translations, that made by Robert Copland for Wynkyn de Worde’s edition of 1508, but drew upon Pynson’s edition of 1506 for some additional material.[88] [73] The work continued to be reprinted down to the latter part of the seventeenth century.
The astronomical sections of the Kalender of Shepherdes, though neither quite so clear nor so extensive as those in the Mirrour, are of greater interest to us because they reached a far wider audience. Not only was the Kalender itself extremely popular, but also, about 1532, Robert Wyer, in that period the most flourishing printer of small handbooks of knowledge for the middle classes, extracted the astronomical and astrological portions from the 1528 edition of the Kalender and reprinted them in a little octavo booklet entitled The Compost of Ptholomeus, Prynce of Astronomye. This sort of piracy seems to have been characteristic of Wyer, who got the material for his cheap manuals of scientific learning in the easiest way possible.[89] All that he did in the case of his Compost of Ptholomeus was to change the word “Shepherd,” wherever it occurred in the text, to “Ptholomeus” or “Astrologian,” and then he proceeded to reprint word for word from the Kalender. A good example of the sort of astronomical learning that was set forth both in the Kalender and Wyer’s Compost is found in the section on the movements of the planets:
Some mouyngs ben of the skyes and planettes/ that excedeth the vnderstādynge of the Astrologyens as the mouynge of the fyrmament: in the which ben the sterres agaynste the firste mobyle in an hondred yere one degre/ and the mouynge of the planettes in theyr epicycles/ of the whiche howe well that Astronomyers be nat ygnoraunt of all/ yet they make no mencyon here/ for it suffyseth them onely of two/ Whereof the one is from oryent in to the occydent aboue the erth/ and from occydent in to the oryent vnder it/ that is called the dyurnall mouynge/ that is to saye that it maketh from daye to daye .xxiiii. houres/ by the whiche mouynge the .ix. skye/ that is the firste mobyle draweth after/ & maketh the other skyes to tourne that ben vnder it. [74] The other moment is of the .vii. Planettes/ and is from occydent to oryent aboue the erthe: and from oryent in to the occydent vnder it/ and is contrary to the firste/ & ben the two mouynges that Astrologyens knowlegeth/ and howe well that they ben opposytces/ yet moue they contynually/ and ben possyble/ as it is shewed by ensample. If a shyp on the see came from oryent in to occydent/ & that he of his owne mouynge went in the shyp softely towarde oryent/ this man shuld moue a double mouynge whereof one shulde be of the shyp and of hymselfe togyder: & the other shuld be of his owne mouynge that he maketh softly towarde orynet [sic]. Semblably the planettes ben/ transported with theyr skye from oryent in to occident by the dyurnall mouynge of the firste mobyle. But later and otherwyse than the fyxed sterres/ by that that euery planet hath his propre mouynge contrary to the mouynge of sterres: For the moone maketh a course lesse in a moneth aboute the erth than a sterre fyxed/ & the sonne a course lesse in a yere: and the other planettes in certayne tyme eche/ after the quātyte of his mouynge. Thus it apperyth that the planettes moue two mouynges. Ptholomeus saythe/ pose by ymagynacion that all the skyes seased to moue of the dayly mouynge/ the moone wolde make a course in goynge from the occydent in to the oryent in as moche tyme as lasteth now .xxvii. dayes/ and .viii. houres/ and Mercury/ Venus/ and Sol wolde make in lyke maner course in the space of a yere/ and Mars in two yere/ and Saturne in .xxx. yere or theraboute. For now they make theyr course or reuolucions: & accomplysshe theyr propre mouynges in the tyme here named. The propre mouynge of planetts is nat streyghte from occydent to oryent/ but it is a syde waye/ and Astrologyens se them sensyble/ For whan they se the moone before a sterre one nyght/ the seconde/ or the thirde nyght/ it is behynde nat streyghte towarde oryent/ but shall be drawen one tyme towarde Septemtryon/ and another tyme towarde mydday/ & this is bycause of the latytude or largenes of the Zodyake/ in the whiche ben the .xii. sygnes/ vnder whom the planttes [sic] reygneth.[90]
The Compost of Ptholomeus was a “best-seller” in its day, but of its many editions only a very few copies have survived.[91] For the members of the middle classes unable to afford the [75] larger encyclopedias, it became the chief source of astronomical knowledge during the first half of the sixteenth century. Robert Wyer also published another little book containing discussions of astronomical problems. Like the Compost, it was a small octavo. The date of its printing is uncertain, but was after 1536; at least, the colophon of the only surviving copy was the one used by Wyer after that date. The volume is entitled, The Boke of Demaundes, of the scyence of Phylosophye, and Astronomye, Betwene kynge Boctus, and the Phylosopher Sydracke. It contains a collection of questions and answers, chiefly on astronomical topics, such as the cause of the moon’s phases, of eclipses, the size and shape of the earth, and the like. Here, again, Wyer has extracted his material from another source: a much larger, better printed, and hence more costly book, The history of kyng Boccus & Sydracke.[92] This work, printed about 1530, is in Skeltonic verse, and consists of a prologue and three hundred and sixty-five questions and answers on matters relating to theology, ethics, philosophy, and natural science. Wyer has selected the questions dealing with astronomy and astrology, and had them paraphrased in awkward prose.
Wyer’s crude books certainly did not greatly advance the cause of the science of astronomy, but they indicate the extent of the interest in astronomical matters among the middle classes.[93] There was, however, a more strictly scientific, though rather specialized and technical, work written in English that saw its first printing at about the same time as Wyer’s handbooks. This was Chaucer’s Treatise on the Astrolabe, which was included by Thynne in his edition of Chaucer’s works, printed in 1532.[94] But this book dealt only with the use [76] and operation of a scientific instrument, and Chaucer left it unfinished, never reaching the fourth part, which he promised “shal ben a Theorike to declare the moeving of the celestiall bodies with the causes.”
The poor quality of the discussions of the science of astronomy in the English language prior to 1543 has been made clear enough by the examples cited. England could boast of no important original work on astronomy, nor any good textbook adequately setting forth its fundamental principles. Yet it would be a serious error to assume that these vernacular works gave a true indication of the state of astronomical learning in England. In this earlier period scholars had not yet begun to adopt the English tongue for learned treatises and textbooks on the sciences. The vernacular movement in scientific writings did not get under way until the 1540’s, but from that time onwards it gained in scope and influence until the end of the century. The first important astronomical books belong to the next decade, and are the work of Robert Recorde (1510?-1558) and John Dee (1527-1608), two learned scholars who were completing their university training at the time of the publication of Copernicus’ De revolutionibus.
Recorde and Dee were universally recognized as the two founders of the school of able mathematical scientists which arose in England during the last half of the sixteenth century. Nearly every subsequent writer acknowledged his indebtedness either to their books or to their personal teaching. The work and influence of Recorde and Dee will be discussed at length in Chapter V; here it is important to understand the long tradition of English scholarship in mathematics and astronomy to which these men and their friends and followers were the conscious and grateful heirs. Recorde and Dee certainly owed much of their attitude towards science and its problems to their study of the works of their English predecessors, and freely testified to this obligation in their writings. They both traced their scientific ancestry back to Roger Bacon.
The respect of these sixteenth-century scientists for Roger Bacon and his successors serves to remind us of the pre-eminence [77] of England in mathematics and astronomy in the thirteenth and fourteenth centuries. Her former leadership in these sciences must be taken into account in estimating the state of mathematical learning in the early Tudor period. We must recall that, at the very time when scholastic philosophy was conquering Europe, the spirit of experimental science and the devotion to the Platonic conception of the importance of mathematics as the key to the secrets of the material world were being preserved by English scholars.
Throughout the Middle Ages the only great work of Greek philosophy known in the West was the Timaeus, available in the Latin translation and commentary of Chalcidius. Before the rediscovery of Aristotle’s scientific works late in the twelfth century, the Timaeus, together with the mathematical textbooks of Boethius[95] and Macrobius’ commentary on the Somnium Scipionis of Cicero, were the most influential writings on the mathematical and physical sciences. Then, with the recovery of Aristotle, the thirteenth-century Schoolmen at the University of Paris developed a “natural theology” which was a synthesis of the Aristotelian, rather than the Platonic, scientific philosophy and Christian theology. This synthesis, chiefly the work of Thomas Aquinas, resulted in the enthronement of Aristotle as the infallible dictator in all natural philosophy. The consequent attitude of the Schoolmen toward science, wherever the Thomist influence predominated, was one that was inimical to progress. According to an eminent student of Platonism, the two things missing in this new Scholastic conception of science were:
(1) the Platonic conviction that the basis of any satisfactory physical science must be sought in mathematics, and (2) the Platonic [78] sense of the provisionality of all results attained in physical science and the consequent necessity of systematic and accurately registered experimentation if we are to be duly acquainted with the ‘appearances’ to be ‘saved’ by scientific theory.[96]
Both of these points were kept in the forefront by the leading scholars in thirteenth-century England, Robert Grosseteste and Roger Bacon. In England the Aristotelianism of Thomas Aquinas never completely displaced the earlier Platonism, and the attitude toward mathematical and experimental science that was implicit in Plato’s philosophy made possible a full utilization of the scientific knowledge of the ancients, then becoming available after the lapse of many centuries through the recovery of the works of the Greeks and the Arabs. The truly scientific spirit of Grosseteste and Bacon, and of their contemporaries at Oxford, was of tremendous significance, coming just at the time when the University of Paris was abandoning the mathematical sciences and turning its back on experimental methods. Professor A. E. Taylor goes so far as to say:
We have probably to thank the independent attitude of the University of Oxford for the very preservation to Europe of mathematics and physical science during the critical time while the resounding success of St. Thomas was turning the minds of the ablest men in the University of Paris to the employment of philosophy in the construction of natural theology and the refutation of the ‘infidel.’[97]
The devotion to the mathematical sciences characteristic of Bacon and Grosseteste was passed on to a long succession of scholars at Oxford. It can rightly be said that “the influence of his [Bacon’s] thought is clearly discernible in Oxford teaching up to the time of the Renaissance.”[98] In the fourteenth century the fame of the group of mathematicians and astronomers [79] which flourished at Merton College was unrivaled in Europe. Among the most famous of the Oxford scientists of this period were Richard of Wallingford, Simon Bredon (Biridan), John Maudith, William Rede, John Ashenden, and Thomas Bradwardine.[99]
The fifteenth-century astronomers at Merton College were a less distinguished group,[100] but there can be little doubt that they kept alive the tradition of scientific teaching, and passed on the ideas of their more noted predecessors. To this period probably belongs William Batecumbe, about whom little is known except the lists of his works given by Leland[101] and Bale,[102] and the fact that he seems to have been connected with Oxford in the fifteenth century. Batecumbe’s writings were chiefly on astronomy, and Bale states that he had examined a copy of one of them in the library of Robert Recorde. Another of his treatises is listed among the manuscripts belonging to John Dee.[103]
The presence of manuscripts of Batecumbe’s works in the libraries of the two most eminent English scientists of the mid-sixteenth century indicates that there was a far greater continuity in English scientific scholarship than has commonly been supposed. If works by earlier men of such comparative obscurity as Batecumbe were known and studied in the sixteenth century, we may well expect the influence of Bacon, Grosseteste, and their fourteenth-century successors on English scientific thought to have been practically uninterrupted. We [80] can prove that their writings were familiar to all the ablest scientists of the Tudor period. For example, if one runs through the list of Dee’s manuscripts, one is struck by the fact that works by Roger Bacon outnumber those by any other author. Manuscripts of Grosseteste are numerous, and the various fourteenth-century English mathematicians and astronomers are well represented.
Other English scientists of the Tudor period, notably Leonard and Thomas Digges, proclaim their indebtedness to Bacon’s works, and indicate that manuscripts of his treatises were greatly prized by scholars and zealously studied with the aim of repeating and amplifying his experiments. Thomas Digges, speaking of his father’s early experiments with the telescope, states:
. . . he was able by Perspectiue Glasses duely scituate vpon conuenient Angles, in such sorte to discouer euery particuliaritie in the Countrey rounde aboute, wheresoeuer the Sunne beames mighte pearse: As sithence Archimedes, (Bakon of Oxforde only excepted) I haue not read of any in Action euer able by meanes natural to performe ye like. Which partly grew by the aide he had by one old written booke of the same Bakons Experiments, that by straunge aduenture, or rather Destinie, came to his hands, though chiefelye by conioyning continual laborious Practise with his Mathematical Studies.[104]
Another indication of the continuity of English mathematical and astronomical learning is found in the list of astronomical writers which Robert Recorde, in 1556, recommends to the student. After mentioning Cleomedes, Proclus, Sacrobosco, Oronce Finé, and Stöffler, he says: “Dyuers Englyshe menne haue written right well in that argument: as Grostehed, Michell Scotte, Batecombe, Baconthorpe, and other dyuers, but fewe of their bookes are printed as yet, therefore I will staye at those three for this tyme.”[105]
The scientists of sixteenth-century England were indeed fortunate in the tradition of learning and the spirit of independent research that they inherited from their compatriots of an [81] earlier era. They were likewise favored by the sympathetic attitude toward the mathematical sciences that was characteristic of most of their leading humanists of the late fifteenth and early sixteenth centuries. The scholars who played the leading part in the revival of Greek learning in England did not confine their interest solely to literary works, but lent their support to the promotion of scientific knowledge and the study of the ancient Greek texts of treatises on mathematics and astronomy. They were well aware that the first requisite for the progress of science was a more accurate and more widely disseminated knowledge of what the Greeks had discovered, so that scholars could apply themselves intelligently to the verifying and augmenting of the body of scientific data that was their heritage from the ancient world. Without subscribing in any way to the idea that the ancient writers were infallible, these scholars were eager to determine the exact meaning of their works. This led them to seek out Greek manuscripts, and to abandon the earlier Latin texts, which had so often been greatly corrupted by successive translations from Greek, to Arabic, to Latin. Once a satisfactory Greek text was discovered, the next task was to make it available to all scholars. Here full advantage could be taken of the recently discovered art of printing, either to multiply copies of the rare Greek manuscripts, or to publish new translations in Latin, made directly from the original Greek. Not until accurate texts of the whole corpus of ancient science had been made accessible to the learned scientists throughout Europe could there be an adequate foundation for rapid progress. In the history of science the great achievement of the early sixteenth century was its making fully effective the Renaissance recovery of the scientific treatises of the ancient world.[106]
In this necessary work of making Greek science more accurately and widely known, no man had a greater share than Thomas Linacre (circa 1460-1524), the earliest of the great English humanists. Linacre directed his classical scholarship almost wholly to scientific ends. His name is pre-eminent in the history of medicine in England, not only as the founder of the College of Physicians in 1518 and of lectureships in medicine at Merton College, Oxford, and St. John’s College, Cambridge, but also as the author of numerous Latin translations of Galen’s works. In the physical sciences, in addition to the Sphaera of Proclus, which has already been mentioned,[107] he translated commentaries on Aristotle’s Physica and Meteorologica; but these remained unpublished.[108]
Of the other noted English humanists, including Linacre’s friends, Grocyn and Latimer, and the slightly younger group composed of Sir Thomas More, John Colet, and Cuthbert Tunstall, only Tunstall, apparently, made any original contribution to mathematical or astronomical scholarship. All, however, were in sympathy with scientific learning, and did not share the scholastic idolization of Aristotle. Instead, their attitude was one of eagerness to recover the genuine Greek texts of all the ancient scientific works, in order not only to get at the true Aristotle but also to compare his ideas with those of other writers so as to determine which of the ancient theories best agreed with reason and observation. This spirit of intelligent, unprejudiced criticism of all earlier authors was the one which dominated English scientific thought for the rest of the century. The conception of science which it implied was fundamentally that of Plato, rather than that of scholastic Aristotelianism, and it is noteworthy that the sixteenth-century [83] English humanists were, on the whole, students and admirers of Plato in preference to Aristotle. Colet and More, in fact, were ardent neo-Platonists, who gave to Ficino and Pico della Mirandola a pre-eminent place among their favorite authors.[109] More, indeed, translated the life of Pico in 1504-5, and published it shortly afterward under the title of The Life of Iohn Picas, Earle of Mirandula.[110]
More, it seems, was attracted chiefly by the ethical and moral elements in Plato, rather than by the Pythagorean aspects of his philosophy; but his friend, Cuthbert Tunstall (1474-1559), who was Master of Rolls under Henry VIII and later Bishop of London and of Durham, was not only an able Greek scholar but also noted for his mathematical learning.[111] In order to improve the quality of arithmetical teaching, Tunstall wrote a lengthy Latin textbook on that subject, De arte supputandi libri quattuor,[112] which he dedicated to Sir Thomas More.
The writings of Sir Thomas More, and the lives by Roper, Harpsfield, and Stapleton, his early biographers, all bear witness to his keen interest in science and especially in astronomy.[113] King Henry VIII often drew upon More’s knowledge of these subjects for his own instruction. Roper tells us that “in the night would he [the King] have him up into the leads, there to consider with him the diversities, courses, motions, and operations of the stars and planets.”[114] Mathematics and astronomy [84] were among the principal subjects of study in More’s household. The astronomical tutor to More’s children was Nicholas Kratzer, a noted scientist of the day who had lectured on astronomy at Oxford before joining More’s circle at Chelsea. More’s ward, Margaret Gigs, who married John Clement, was famous for her profound scientific learning.
In view of More’s keen personal interest in science, there is little wonder that he did not confine his patronage of classical scholars to those who were engaged in editing or translating literary works, but gave equal encouragement to scientific studies. Of special importance to us is the aid given to Simon Grynaeus, the scholar who supervised the first Greek editions of the most important works in mathematical science left us by antiquity, Euclid’s Elements and Ptolemy’s Almagest. Grynaeus visited England in 1531 and was cordially received by Tunstall, More, and the other scholars at Henry’s court, and was entertained in More’s household. Two years later, in 1533, the first Greek edition of Euclid, under Grynaeus’ editorship, was published at Basel and dedicated to Cuthbert Tunstall. In 1534 the second edition of the Greek text of Plato’s works, together with Proclus’ commentary on the Timaeus and Diogenes Laërtius’ life of Plato, was published at Basel under Grynaeus’ supervision. In the dedicatory epistle, addressed to John More, Sir Thomas’ son, Grynaeus speaks of his entertainment at the Chancellor’s house during his English sojourn:
I was there received with great kindness, was entertained with greater, was dismissed with the greatest of all. For that great and excellent man your father, so eminent for his high rank and noble talents, not only allowed me, a private and obscure person (such was his love of literature), the honour of conversing with him in the midst of many public and private affairs, gave me a place at his table, though he was the greatest man in England, took me with him when he went to court or returned from it, and had me ever by his side, but also with the utmost gentleness and candour inquired, in what particulars my religious principles were different from his; and though he found them to vary greatly, yet he was so kind as to assist me in every respect, and even to defray all my expences.[115]
When Grynaeus published the first Greek edition of the Almagest in 1538, Sir Thomas More had already been executed for defying the will of his sovereign. Consequently, the work was dedicated to a new English patron, King Henry himself, to whose favor Grynaeus had been introduced seven years earlier by More.
Another noted scholar who owed much to the patronage of More and his circle was Juan Luís Vives, famous for his advanced ideas on education. In his system of instruction Vives gave a very important place to scientific subjects. His De Tradendis Disciplinis (Antwerp, 1531) discusses at some length the teaching of the mathematical sciences, giving a list of books to be studied which includes most of the best works in print at that time.[116] In the preface to this book, Vives, while professing sincere respect for Aristotle, vigorously asserts the right to criticize all opinions received from the ancients, maintaining that “much of truth has been left for future generations to discover.”[117]
Vives was also an ardent advocate of directing all studies toward practical and useful ends, and placed a high value on the works written in the vernacular for the wider dissemination of knowledge. Similar ideas were proclaimed by another important member of More’s circle—his brother-in-law, John Rastell. In his A new interlude and a mery of the nature of the .iiij. elementes,[118] Rastell made an earnest plea for the use of English in learned scientific works, and for the translation into [86] English of the best ancient books on scientific subjects. This interlude, written and published shortly after 1517, was really a lesson in the fundamentals of astronomy and cosmography, disguised in dramatic form. The character, “Experyence,” representing the experimental scientist, even brings his instruments on the stage to demonstrate his conclusions. The Messenger’s speech at the beginning of the play is most significant. Through his lines Rastell makes a stirring appeal for the use of the English language in works of solid learning, inveighs against the lack of anything but trifling books in the vernacular, and maintains that English is now fully equal to the task of conveying the most abstruse philosophical and scientific ideas. The Messenger makes the customary apologies for the author, and continues:
yet the auctour hereof requiryth you all
Though he be yngnorant and can lytyll skyll
To regarde his only intent and good wyll
¶whiche in his mynde hath oft tymes ponderyd
what nombre of bokes in our tonge maternall
Of toyes and tryfellys be made and impryntyd
And few of them of matter substancyall
For though many make bokes yet vnneth ye shall
In our englyshe tonge fynde any warkes
Of connynge that is regardyd by clerkes
¶The grekes the romayns with many other mo
In their moder tonge wrot warkes excellent
Than yf clerkes in this realme wolde take payn so
Consyderyng that our tonge is now suffycyent
To expoun any hard sentence euydent
They myght yf they wolde in our englyshe tonge
wryte workys of grauyte somtyme amonge
¶For dyuers prengnaunt wyttes be in this lande
As well of noble men as of meane estate
whiche nothynge but englyshe can vnderstande
Than yf connynge laten bokys were translate
In to englyshe/ wel correct and approbate
All subtell sciens in englyshe myght be lernyd
As well as other people in their owne tonges dyd[119]
The importance of Sir Thomas More and his circle in the early history of the English drama has recently been established by Professor A. W. Reed,[120] and Professor R. W. Chambers has pointed out the significant position of this same group in the development of English prose.[121] It would be interesting if the beginnings of the vernacular tradition in English science could also be definitely traced to More’s circle. Some of the original inspiration may well be due to these men, for Rastell’s plea in the Interlude of the Four Elements would seem to indicate as much. Except for this work of Rastell’s, however, More’s family and friends apparently did little toward furthering the praiseworthy aim of making scientific learning available to Englishmen in their own language, but left the task for later generations of their countrymen. Perhaps one reason for their failure in this respect may have been the realization that the recovery and publication of the original texts of the chief Greek scientific treatises was an essential preliminary to the task of translation. We have just seen that their support and patronage were freely given to the scholars engaged in this indispensable preparatory work.
The group of English humanists, and More’s circle in particular, were the chief promoters of both classical scholarship and scientific learning in the early sixteenth century. Their influence was interrupted, however, by More’s execution and the voluntary exile of most of his friends and followers. It is difficult to estimate the importance of this check to the normal flow of scientific progress in England. Certain it is, however, that except for the loss of support at the court the setback was only temporary. A new generation of scholars soon arose which, while not regaining for England her former international pre-eminence, kept the enthusiasm for learning alive in that country. This generation, in which the two most prominent figures were Sir John Cheke (1514-1557) and Sir Thomas [88] Smith (1513-1577), made Cambridge University, and especially the colleges with which they were associated, inspiring centers of classical study during the fourth and fifth decades of the sixteenth century. Through their students their influence was passed on and dominated English scholarship for the remainder of the century.
Both Cheke and Smith were ardent believers in the value of Greek studies, and gave the scientific works in that language a prominent place in their own teaching. Cheke, who was to become in 1540 the first Regius Professor of Greek, was a fellow of St. John’s College[122] from 1530 to the summer of 1544, when he joined the court as tutor to Prince Edward, later Edward VI. He still maintained contact with the university, however, and, after his election as Provost of King’s College in 1548, returned to Cambridge from time to time to direct the affairs of the college. Richard Mulcaster, who was a student at King’s College at the time, gives the following account of Cheke’s encouragement of mathematical studies:
The worthy, and well learned gentleman Sir Iohn Cheeke, in the middest of all his great learning, his rare eloquence, his sownd iudgement, his graue modestie, feared the blame of a mathematicall head so litle in himselfe, and thought the profession to be so farre from any such taint, being soundly and sadly studied by others, as he bewraid his great affection towards them most euidently in this his doing. Being himselfe prouost of the kings colledge in Cambridge, in the time of his most honored prince, and his best hoped pupill, the good king Edward, brother to our gracious soueraine Queene Elizabeth, he sent downe from the court one maister Bukley somtime fellow of the saide colledge, and very well studyed in the mathematicalls to reade Arithmeticke, and Geometrie to the youth of the colledge: and for the better encouraging of them to that studie gaue them a number of Euclides of his owne coast. Maister Bukley had drawne the rules of Arithmeticke into verses, and gaue the copies abroad to his hearers. My selfe am to honour the memorie of that learned knight, being partaker my selfe of his liberall distribution of those Euclides, with whom he ioyned Xenophon, which booke he wished, and caused to be red in the same house, and gaue them to the studentes, to encourage them aswell to the greeke toungue, as he did [89] to the mathematikes. He did I take it asmuch for the studentes in S. Iohns colledge, whose pupill he had once bene, as he did for vs of the kinges colledge whose prouost he then was. Can he then mislike the mathematicall sciences, which will seeme to honour Syr Iohn Cheeke, and reuerence his iudgement?[123]
Sir Thomas Smith, who became a fellow of Queens’ College in 1529, lectured on natural philosophy in the schools, and on Greek in his own rooms. He traveled abroad from 1540 to 1543, studying at Paris, Orleans, and Padua, and on his return became the first Regius Professor of Civil Law at Cambridge. In addition to his Greek and legal studies, he was an able scholar in astronomy. Gabriel Harvey, his fellow townsman, in the memorial volume he published after Smith’s death,[124] particularly emphasizes Smith’s skill in the mathematical sciences, and, above all, in astronomy, proclaiming him greater than Ptolemy and a hundred Alfonsos.
During his life Smith gathered together a remarkable library, which included most of the important mathematical and astronomical works of his day. The catalogue of “Sir Thomas Smith’s library, Aug. 1, 1566, in his gallery at Hillhall,” is published by Strype in his life of Smith.[125] It lists a copy of the first edition of Copernicus’ De revolutionibus. The date on which Smith acquired this book cannot be determined, but he may well have heard of Copernicus’ forthcoming work during his travels abroad, or through the advance notices given by Rheticus and Reinhold, and have obtained his copy soon after publication. Among the other astronomical treatises he owned, the most important were the first Greek edition of the Almagest, the works of Euclid and Archimedes, of Peter Apian, [90] Gemma Frisius, Regiomontanus, and John Stöffler, and the Prutenic Tables of Reinhold.
It must be remembered that in the early sixteenth century a mastery of Greek was recognized as an indispensable part of the equipment of any scholar interested in the sciences. Men realized that a first-hand knowledge of the ideas and discoveries of the ancient scientists was the foundation upon which further progress must be based, and that the Greek language was the necessary key to such knowledge. Thus, although Cheke and Smith did not themselves make any original contributions to science, their teaching and influence at Cambridge played a significant part in training the men who were to be among the early leaders in the new scientific movement in England. Robert Recorde, after taking his B.A., and probably his M.A., at Oxford, transferred to Cambridge, where he took the degree of Doctor of Medicine in 1545. He was therefore present at the university during the very period when the influence of Cheke and Smith was at its height. The details of his connections with Cambridge are unknown, but his later works show him as a thorough Greek scholar, who had studied the principal scientific writings in their original texts.[126]
John Dee, the other chief founder of the English scientific school, matriculated at St. John’s College, Cambridge, in 1542. This was Cheke’s own college, and Dee, therefore, came under his influence and doubtless was one of his pupils. After leaving for the court, Cheke kept in touch with Dee’s progress. In 1551, after the latter’s return from a visit to the University of Paris, where he had created a sensation by reading “freely and publiquely Euclide’s Elements Geometricall, Mathematicè, Physicè et Pythagoricè; a thing never done publiquely in any University of Christendome,”[127] Cheke secured for him the patronage of Edward VI, through the Secretary of State, William Cecil, Cheke’s brother-in-law.[128]
William Cecil, later Lord Burghley and Treasurer under Queen Elizabeth, had also been one of Cheke’s pupils at Cambridge, and owed to him his interest in classical and scientific scholarship. Other noted Englishmen who had studied under Cheke, besides Richard Mulcaster (already mentioned), were William Bill, Roger Ascham, and probably Anthony Ascham, the writer on astronomy. Bill had also been a pupil of Sir Thomas Smith’s, along with Richard Eden and John Ponet. All of these men were famous among their contemporaries for their mathematical and scientific, as well as their classical, learning.[129] Bill was physician to Henry VIII and Edward VI. Eden became one of the most important translators of scientific works dealing with navigation and the New World,[130] and also assisted Geminus in preparing the 1559 edition of his Compendium of Vesalius.[131]
Roger Ascham, in his later years, was inclined to give the mathematical sciences a much lower place in comparison with classical literature than any of the other noted scholars among Sir John Cheke’s pupils. It must be remembered, however, that in 1539 Ascham had earnestly sought for himself a mathematical lectureship at the University of Cambridge, so that mathematics had certainly not been omitted from his early studies with his master. In our present study, Roger Ascham’s chief importance lies in his connection with the establishment, in England, of the vernacular tradition for technical and scientific exposition. His Toxophilus (1543) is one of the earliest examples of an eminent and learned scholar’s turning to the [92] English language when writing a work of that sort, with the avowed aim of making technical knowledge available to his less learned countrymen. For this purpose, Ascham deliberately cultivated a direct and simple style, following, as he says, “thys councel of Aristotle, to speake as the cōmon people do, to thinke as wise men do: and so shoulde euery man vnderstande hym, and the iudgement of wyse men alowe hym.”[132] The aims and the theories of vernacular style that Ascham thus proclaimed in his Toxophilus were the same as those so enthusiastically adopted by Recorde and the other English scientific writers who followed him.
The system of cosmology that prevailed in the early sixteenth century has been described in some detail in Chapter II. The method there followed consisted, first, in making clear the nature of the astronomical phenomena which any system had to account for in order to maintain itself among thorough students of the stellar motions; and, second, in tracing the historical evolution of the various elements that went to make up the conception of the universe generally accepted in 1543. My purpose in following this method was twofold. On the one hand, by means of a historical analysis, I sought to make clear the true nature of the traditional cosmology, setting forth the causes which led to its creation and development. On the other hand, I endeavored to portray the diverse elements which lay behind most pre-Copernican theories concerning the system of the universe, in order to reveal the attitude of various groups towards the new heliocentric system, and to define more exactly what modifications of old beliefs were necessary before a sixteenth-century Englishman would be prepared to accept the Copernican hypothesis.
Most of the misunderstanding in the past concerning the effect of the new astronomy on sixteenth-century thought has been due to a lack of appreciation of the composite character of the so-called Ptolemaic system, and to a failure to realize that certain intellectual forces were already producing a disintegration of the old cosmological beliefs. The history of astronomical thought during the hundred years following the publication of the De revolutionibus is one of progressive modification of the traditional ideas because of the impact of new theories and discoveries. Without a thorough preliminary analysis of the scientific foundations of the geocentric astronomy, [94] it would be impossible either to sift the old notions from the new as they turn up in the astronomical literature of the sixteenth and seventeenth centuries, or to recognize the significance of the modifications that gradually crept into even the most conservative treatises on cosmological doctrines. Similarly, a clear conception of the four most important elements out of which the Renaissance theories of the universe were evolved is essential. Only thus can we comprehend the inter-relation between the intellectual forces which were to be engaged in the struggle over the transferring of the center of the world from the earth to the sun.
In surveying the chief constituents of pre-Copernican cosmological ideas—Aristotelian physics, Christian theology, Ptolemaic mathematics, and neo-Platonic philosophy—it becomes clear that this order represents the relative zeal with which the partisans of each of these four currents of thought would feel impelled to defend the old astronomical system. At the core of that system lay the physical theories of Aristotle, and the Aristotelians had adopted the mathematics of Ptolemy only after transforming his abstract constructions into material spheres. To accept the new system meant denying some of the fundamental postulates of Aristotelian natural philosophy, and all those who believed in Aristotle’s infallibility were bound to oppose Copernicus to the last. The theological dogmas of the Church, however, were not so inextricably involved with the old astronomy as to make acceptance of the heliocentric theory impossible. The synthesis of Christian theology and Aristotelian science made by the Schoolmen of the thirteenth century was the chief barrier which prevented the Church from being entirely neutral concerning the new astronomical doctrines. Had the Christian theologians not previously committed themselves to Aristotelian science, they would have found no great difficulty in reconciling passages in the Scriptures with the ideas of Copernicus. The idea that these passages were to be interpreted figuratively, as statements of the way things appeared to the common man rather than as scientific truths, had already been invoked when the Church [95] had made a place in its theology for the basic axioms of Greek science. By no other means could the references to the “four corners of the earth” and to the sun and moon as the “two great lights” have been brought into accord with Greek astronomy, with its spherical earth and its geometrical proofs that the moon was actually smaller than the planets.
The Aristotelians, therefore, together with the less liberal theologians, could be depended upon to oppose the Copernican theory. The mathematicians, on the other hand—at least the abler ones who had mastered Ptolemy’s own work rather than derived their knowledge of it at second hand, from the Arab commentators—could be expected to be very tolerant toward the new hypothesis. The old system, based upon Ptolemy’s able mathematical treatment of the facts of the heavenly motions, had been growing increasingly complex as new inequalities were discovered and taken into account. Therefore, any simplification of this system that was both mathematically sound and an adequate representation of the known observational data would be welcomed by the mathematicians. The Aristotelians among them might deny its physical truth, and yet accept it because it “saved the phenomena” and was a valuable short cut in astronomical calculations. On the other hand, those who were profoundly influenced by neo-Platonism would be inclined to adopt it without qualification. In the first place, the neo-Platonists had put forward Plato and the pre-Socratic philosophers as authorities equal to Aristotle, or even greater. The fact that the new hypothesis contradicted Aristotelian dogmas would not condemn it in their eyes. Furthermore, the neo-Platonic philosophy included the Pythagorean belief in the fundamentally mathematical structure of the universe. The notion that number was “the first model of things in the mind of the Creator” and that explanations of material phenomena were to be sought in the harmonious mathematical relationships discoverable in them, was the basis of Pythagoreanism. Hence, to the Renaissance neo-Platonist, the simplest and most harmonious mathematical system capable of representing the facts would, by virtue of those very qualities, [96] be closest to reality, and consequently the most acceptable system.
It was among the fifteenth-century neo-Platonists, therefore, that the greatest dissatisfaction had arisen with the increasing complexity of the Ptolemaic system. This same school of philosophers were also the most eager students of those ancient speculations concerning the universe which disagreed with the theories of Aristotle, and were responsible for giving these older ideas a prominent place in current discussions of cosmology.
When Nicholas Copernicus (1473-1543) went to Italy, he plunged into an intellectual atmosphere surcharged with neo-Platonic ideas. During his stay south of the Alps (which, with minor interruptions, lasted for over nine years, from 1497 to 1506), Copernicus not only became acquainted with the postulates of Pythagorean philosophy but also made himself thoroughly familiar with the early Greek astronomical speculations, in so far as they were then known in Europe. His friend and teacher at the University of Bologna, where he studied for several years, was Domenico Maria da Novara, an ardent neo-Platonist who fully subscribed to the Pythagorean doctrines and vigorously criticized the existing Ptolemaic astronomy for its cumbrous complexity.[133] Doubtless because of Novara’s influence, Copernicus conceived the idea of devoting himself to the task of working out a new and simpler geometrical system of astronomy, which would overcome the current objections to Ptolemy and be in closer accord with the neo-Platonic idea that the universe was designed by the Creator in terms of harmonious mathematical laws.
Copernicus, through his extensive reading in the astronomical theories of the past, beginning with the references to the earliest Greek hypotheses, and extending through the works of the Arabian astronomers down to the writings of his immediate predecessors, was able to determine for himself the precise nature of his problem. The ancient systems which [97] assigned motions to the earth, either of rotation about its axis or of revolution about some other body, or both, gave him his most useful clue. The question, as he eventually defined it, was: If we assume that the earth rotates about its axis and revolves in an orbit about the sun, what mathematical consequences will follow from this assumption; and can a system be worked out mathematically on this basis which will be just as adequate as the Ptolemaic system and much more simple? His great work, the De revolutionibus orbium coelestium,[134] published in 1543, gave his affirmative answer to the last part of this question. The course of Copernicus’ thinking with reference to the astronomical ideas of the past is clearly indicated in the preface and in the first book of his work. His knowledge of Heraclides’ theory of the earth’s rotation, and of the system of Philolaus, is evident in the following passage:
Since the heavens which contain and retain all things are the common home of all things, it is not at once comprehensible why a motion is not rather ascribed to the thing contained than to the containing, to the located rather than to the locating. This opinion was actually held by the Pythogoreans Heraclides and Ecphantus and the Syracusean Nicetas (as told by Cicero), in that they assumed the earth to be rotating in the center of the universe. They were indeed of the opinion that the stars set due to the intervening of the earth, and rose due to its receding. . . .
It would thus not be strange if someone should ascribe to the earth, in addition to its daily rotation, also another motion. However, it is said that the Pythagorean, Philolaus, a not ordinary mathematician, believed that the earth rotates, that it moves along in space with various motions, and that it belongs to the planets; wherefore, Plato did not delay journeying to Italy to interview him, as is told by those who have described Plato’s life.[135]
In the tenth chapter of the first book of the De revolutionibus, headed “De ordine coelestium orbium,” Copernicus briefly surveys the previous planetary systems, as a preliminary to describing and giving arguments for his own. I quote from the English translation published by Thomas Digges in 1576, because this was the version familiar to Elizabethan England.
And of these strayinge bodyes called Planets the old philosophers thought it a good grounde in reason yt the nighest to the center shoulde swyftlyest mooue, because the circle was least and thereby the sooner ouerpassed and the farder distant the more slowelye. Therefore as the Moone beinge swyftest in course is founde also by measure nyghest, so haue all agreed yt the Orbe of Saturn being in moouinge the slowest of al ye Planets, is also the highest: Jupiter the next, and then Mars, but of Venus & Mercury ther hath bene great controuersie, because they stray not euery way from the Sūne as the rest doo. And therefore some haue placed them aboue the Sūne as Plato in his Timaeo: others beneath, as Ptolemy and the greater part of them yt folowed him. Alpetragius maketh Venus aboue the Sunne and Mercury beneath, and sūdry reasons haue bene of al sides alledged in defence of their opinions. They that folowe Plato (supposinge that all starres should haue obscure & darcke bodyes shyninge with borrowed light like the Mone) haue alledged that yf those Planets were lower then the Sun, then should they sometyme obscure some part of the body of the Sunne, and also shyne not with a lyght circulare but segmentary and that varyable as in the Moone: Which when they see by experience at no time to happen, they conclude with Plato. On the cōtrary part sutch as will maynteyn them beneath, frame a likelyhoode by reason of the lardge space betwene the Orbes of Sun & Moon. For the greatest distance of the Moon is but .64.-1/2 semidiameters of the Earth & to the nighest of the Sunne are .1160. so that there remayneth betwene ye Moon and the Sun .1095. semidiameters of the earth. And therefore yt so hudge a space should not remayne emptie, there they situate the Orbes of Mercury and Venus. And by the dystance of their Absides whereby they serche the thicknes of their Orbes they find that they of all the rest best aūswere that situation, so as the lowest of Mercuries Orbe may reache downe almost to the highest of the Moones, & the toppe of Mercury to the inferiour part of Venus sphere, which with his Absis should reach almost vnto the Sunne. For betwene the Absides of Mercury by their Theoricks they supputate .177. semidiameters of the earth and then the [99] crassitude of Venus Orbe beinge .910. semidiameters doth vary nyghe supplye and fill the residue. They therefore will not confesse that these Planets haue any obscuritye in their bodyes lyke the Moone, but that either with their owne proper light or els beinge thoroughly persed with solare beames they shine and shewe Circulare. And hauinge a strayinge course of latitude they seldom passe betwene the Sunne and vs, or yf they should their bodyes beinge so small coulde scarcelye hyde the hundred parte of the Sunne, and so small a spot in so noble a light could hardly bee discerned. And yet Auerrois in his Paraphrasis on Ptolomey affyrmeth that he sawe a litle spot in the Sūne at sutch time as by Calculation he had forecast a corporall Coniunction. . . . Againe yt reason of Ptolomey that the Sun must neades bee placed in the middest of those Planets that wander from him at liberty and those yt are as it were cōbined to him, is proved sensles by ye motiō of the Mone, whom we see no lesse to stray from the Sun then any of those other three superiour Planets. But yf they wyll neades haue these two Planets Orbes within an Orbe of the Sūne, what reason can they geue why they should not depart from ye Sunne at lardge, as the other Planets dooe, consideringe the increase of swiftnes in their motion must accōpany the inferior situatiō, or els ye whole order of Theoricks should be disturbed. Yt is therefore euydent that eyther there muste be some other Centre whereunto the order of these Orbes should be referred, or els no reason in their order nor cause apparāt why we should rather to Saturn then to Jupiter or any of the rest attribute the higher or remoter Orbe. And therfore seemeth it worthy of consideratiō that Martianus Capella wrote in hys Encyclopedia and certayne other latines held, affyrminge that Venus and Mercury dooe runne about the Sunne in their spheres peculiare, & therefore coulde not strey farther from the Sun then the capacity of their Orbes would geue them leaue . . . what other thinge would they heareby signify but yt the Orbes of these Planets should enuiron the Sunne as their Center. So may the sphere of Mercury beinge not of haulfe the amplitude of Venus Orbe, be well situate within ye same. And if in like sorte we situate the Orbs of Saturn Jupiter and Mars referringe them as it were to the same Center, so as theyr capacitye bee sutch as they containe and circulate also the earth, happely we shal not erre . . . For it is apparante that these Planets nigh the Sunne are alwayes least, and fardest distant and opposite are mutch greater in sight & nigher to vs, wherby it cannot be but the centre of them is rather to the Sun then to ye earth to be referred: as in the Orbes of Venus and Mercury also. But yf all these to the Sunne as a centre in this manner bee referred, then must there neades betwene the conuex Orbe of Venus and the concaue of Mars an hudge space be left wherein the earth & Elementare frame enclosed with the Lunare Orbe of duty must be situate. For from the earth the Moone may not be farre remooued, [100] beynge wythout controuersye of all other nyghest in place and nature to it: especially cōsideryng betwene the same Orbes of Venus and Mars there is roome sufficient. Therefore neade we not to be ashamed to confesse this whole globe of Elemēts enclosed with the Moones sphere together wyth the earth as the Centre of the same to be by this great Orbe together with the other Planets about the Sun tourned makinge by hys reuolution oure yeare. And what soeuer seeme to vs to proceede by the mouinge of the Sunne, the same to proceede in deede by the reuolution of the earth, the Sunne stille remayninge fixed & immoueable in the middest. And the distance of the earth frō the Sunne to be sutch as being compared with the other Planets maketh euidente alterations and diuersity of Aspects, but yf it be referred to the Orbe of starres fixed, then hath it no proportion sensible, but as a poinct or a Center to a circumferēce, which I hould farre more reasonable to be graūted, then to fal into sutche an infinyte multitude of absurde ymaginations, as they were fayne to admit that will neades wilfully maynteine the earthes stabilitye in the Centre of the world. . . .[136]
Later in the chapter, Copernicus proclaims, as the great merit of the system he has just expounded, that it is more symmetrical and harmonious than earlier systems, and offers a simpler and more logical explanation of the retrograde motions of the planets:
. . . In this fourme of Frame may we behould sutch a wonderful Symetry of motions and situations, as in no other can bee proponed: The times whereby we the Inhabitauntes of the earth are directed, are constituted by the reuolutions of the earth, ye circulation of her Centre causeth the yeare, the conuersion of her circumference maketh the naturall day, and the reuolutiō of the Moon produceth the monethe. By the onelye viewe of thys Theoricke the cause & reason is apparante why in Jupiter the progressions and Retrogradations are greater then in Saturn, and lesse then in Mars, why also in Venus they are more then in Mercury. And why sutch chandges from Direct [101] to Retrograde Stationarie. &c. happeneth notwithstandinge more rifely in Saturn then in Jupiter & yet more rarely in Mars, why in Venus not so cōmonly as in Mercury. Also whye Saturn Jupiter and Mars are nigher the earth in their Acronicall then in their Cosmicall or Heliacall rysinge. Especially Mars who rising at the Sunne set, sheweth in his ruddy fiery coollour equall in quantity with Iupiter, and contrarywise setting little after the Sunne, is scarcely to be discerned from a Starre of the seconde light. All whiche alterations apparantlye folowe vppon the Earthes motion. And that none of these do happen in the fixed starres, yt playnly argueth their huge dystance and inmēsurable Altitude, in respect whereof this great Orbe wherein the earth is carryed is but a poyncte, and vtterly without sensible proportion beinge compared to that heauen. . . .[137]
These quotations serve to emphasize the way in which Copernicus’ arguments in favor of his theory were consciously directed toward those who, like himself, accepted the tenets of neo-Platonic Pythagoreanism and considered the authority of Plato and the pre-Socratic philosophers equal to that of Aristotle.
Because of the many mistaken notions concerning the true nature of the changes introduced by Copernicus, a detailed analysis of the alterations he made in the older conceptions is necessary. Their essential features may be described quite briefly. Copernicus merely assigned a motion of rotation to the earth, replacing the diurnal rotation of the heavens in the Ptolemaic system, and then made the sun instead of the earth the center of co-ordinates to which all the planetary orbits (except the moon’s) were referred. The sun now became the fixed and motionless body at the center of our universe, and the earth one of the planets revolving about it. On the basis of this new center of co-ordinates, Copernicus proceeded to calculate the elements of the orbits of each of the planets, and to work out methods of representing the various inequalities in the planetary motions. He employed the same geometrical methods that Ptolemy had used, except that he cast aside the equant. The shifting of the center to the sun automatically eliminated one of Ptolemy’s circles for each planet: [102] the principal deferent in the case of the inferior planets, and the principal epicycle in the case of the superior. The main function of these circles had been to represent features of the planetary motions intimately connected with the apparent motion of the sun (according to the Copernican theory, they represented the actual motion of the earth in its orbit about the sun). Along with these principal circles, several minor ones, introduced because of the variable velocity of the sun’s apparent motion (actually due to the eccentricity of the earth’s orbit), were also eliminated. However, when the orbits of the various planets were referred to the sun, it was still evident that these wandering stars did not move uniformly about circles concentric with the sun. The actual eccentricity of their orbits had to be represented, and Copernicus resorted to eccentric deferents and epicycles exactly in the manner of Ptolemy.[138]
Copernicus, therefore, did not do away with Ptolemy’s eccentric and epicyclic circles. He merely reduced the number from some eighty to thirty-four. As a result, the new system was much simpler mathematically, but, aside from the mere change of co-ordinates, not essentially different from the old. The mathematician who had really mastered the Almagest and grasped the principle of the relativity of motion, would feel entirely at home in the De revolutionibus. It was to these learned mathematicians, who were best able to appreciate the relative simplicity and superiority of his system, that Copernicus appealed as the persons qualified to judge the intrinsic merits of his work.[139]
It must be emphasized that Copernicus made no changes in the old system that were not necessitated by his shifting of [103] the center of mathematical co-ordinates and his assigning motions of rotation and revolution to the earth. He did not question the Aristotelian distinction between the ethereal region outside of the moon’s orbit and the sublunary region of the elements surrounding our earth. How far he really believed in this distinction was uncertain, but it had no essential bearing on his new theories, and there was no cause for him to enter into conflict with Aristotelians on this point.
The system worked out in the De revolutionibus provided a new theoretical basis for determining the dimensions of the orbits of the planets in terms of the distance from the earth to the sun. Copernicus calculated the distances of the various planets in accord with his theory, using the mean radius of the earth’s orbit as a unit of measure. His results, expressed in this unit, were very nearly correct.[140] He accepted, however, Hipparchus’ erroneous value of 3′ for the solar parallax, and made the mean distance between the sun and the earth equal to 1142 times the earth’s radius (true value, approximately 23,500 earth radii). Consequently, the dimensions, in miles, of the solar system as pictured by Copernicus were only about one-twentieth of the true figures.[141] Although his computation of the sun’s distance was only very slightly less than Ptolemy’s, his figures for the distances of the planets were considerably less than those calculated by the Arabian astronomers on the theory that the greatest distance of any planet [104] was equal to the least distance of the one next above it.[142] Computed according to Copernicus’ figures, the greatest distance of Saturn would be about 12,000 times the radius of the earth. According to Alfraganus, it was over 20,000 earth radii. Similarly, if one retained the old values for the apparent diameters of the planets, their sizes (except for Mercury, which Copernicus had placed, relatively, much farther from the earth), would likewise become smaller than in the old astronomy, since their distances were less.
Inasmuch as the actual diameters of the planets would decrease in direct proportion to the decrease in their assumed distances, whereas their actual sizes would be proportionate to the cubes of the diameters, the Copernican system made the sizes of the two most distant planets very much smaller than before. Saturn, instead of being computed as 91 times the earth in size, would become only about 20 times as large as the earth, and Jupiter only about 13 times as great.[143]
It is therefore clear that, contrary to our modern impression, the Copernican theory made the dimensions of the solar system much smaller than before. It was only with respect to the size of the sphere of fixed stars that Copernicus increased the previously accepted estimates. Whereas, before, the firmament had been located just beyond the sphere of Saturn, in the Copernican system it had to be placed much farther off, leaving a vast space between. This step was made inevitable by the assigning of motions of rotation and revolution to the earth. In the new system, the sphere of fixed stars was supposed to be motionless, since its apparent movement was fully accounted for by the daily rotation of the earth. Therefore, if the fixed stars were not much farther off than Saturn, there would have to be a considerable change in their relative positions as seen from two points in the earth’s orbit 180° apart. In other words, what is known in astronomy as an annual parallax should be perceptible in these fixed stars. No such parallax could be discovered. Hence it was necessary either to give up the idea of the earth’s revolution about the sun or to assume that the distance of the stars was so great, in comparison with the diameter of the earth’s orbit, as to make the actual parallax too small to be detected by existing instruments. Copernicus freely made this assumption, even though it involved placing the fixed stars at an immeasurable distance.[144]
Other sixteenth-century scientists, however, raised an entirely valid objection to this phase of Copernicus’ theory, maintaining that he was here attempting to overcome a serious difficulty in his system by making a wholly unwarranted assumption. They pointed out that the only way in which the revolution of the earth about the sun could be definitely proved by observational methods was precisely through measuring and verifying the existence of some stellar parallax. This objection was [106] not overcome until 1838, when the first successful determinations of the parallaxes of stars were announced.[145]
Copernicus certainly realized that he might reasonably have maintained that the stars were scattered at infinite distances, throughout an infinite universe. He even went so far as to mention the question of the infinity of the universe when, in Book I, Chapter 8, of the De revolutionibus, he was refuting the Ptolemaic contention that the earth, if it rotated, would soon fly to pieces through the action of centrifugal force.
But whye should hee [Ptolemy] not mutch more thincke and misdought the same of the worlde, whose motion muste of necessity be so mutche more swift and vehemente then this of the Earth, as the Heauen is greater then ye Earth. Is therefore the Heauen made so huyge in quantitye that yt might wyth vnspeakable vehemencye of motion bee seuered from the Centre, least happily restinge it should fall, as some Philosophers haue affirmed: Surelye yf this reason shoulde take place, the Magnitude of the Heauen shoulde infinitely extende. For the more this motion shoulde violentlye bee carryed higher, the greater should the swiftnes be, by reason of the increasing of the circumferēce which must of necessity in 24. houers bee paste ouer, and in lyke maner by increase of the motion the Magnitude muste also necessarilye bee augmented. Thus shoulde the swiftnes increase the Magnitude and the Magnitude the swiftnes infinitely: But according to that grounde of nature whatsoeuer is infinite canne neuer be passed ouer. The Heauen therefore of necessity must stande and rest fixed. But say they without the Heauen there is no body, no place, no emptynes, no not any thinge at all whether heauen should or could farther extende. . . . Yet yf wee would thus confesse that the Heauen were indeede infinite vpwarde, and onely fynyte downewarde in respecte of his sphericall concauitye, Mutch more perhappes might that sayinge be verified, that without the Heauen is nothinge, seeinge euerye thinge in respect of the infinitenes thereof had place sufficient within ye same. But then must it of necessity remaine immoueable. For the cheefest reason that hath mooued some to thincke the Heauen limited was Motion, whiche they thoughte without controuersie to bee in deede in it. But whether the worlde haue his boundes or bee in deede infinite and without boundes, let vs leaue that to be discussed of Philosophers; sure we are yt the Earthe is not infinite but hath a circumference lymitted. Seinge therefore all Philosophers consent that lymitted [107] bodyes maye haue Motion, and infinyte cannot haue anye, whye dooe we yet stagger to confesse motion in the Earth beinge most agreeable to hys forme and nature, whose boundes also and circumference wee knowe, rather then to imagyne that the whole world should sway and turne, whose ende we know not, ne possibly can of any mortall man be knowne.[146]
We see, therefore, that Copernicus declined to commit himself definitely on the question of the infinity of the universe. His real purpose was to revise the arrangement of the planets, and to calculate their motions in accordance with a new system. Hence he refused to be drawn off into metaphysical discussions, leaving those to the “Philosophers.” In his diagram of the universe, he was content to portray the position of the stars by a finite, though motionless, circumscribing circle, inclosing the whole world. He made this sphere of the fixed stars so vast, however, that its surface was sufficiently distant from the center of our solar system for no stellar parallax to be perceptible.[147]
It has been customary to overestimate the effect on contemporary thought of the tremendous enlargement of the magnitude of the stellar sphere which followed from the Copernican theory. Long before the publication of the De revolutionibus, the earth had been considered an insignificant speck in comparison with the universe. It is thus a great mistake to think that man’s place in the old cosmology bulked very large in sixteenth-century eyes. Philosophy and theology might, in certain respects, sanction the idea that the material world had been designed by God to be useful to man and minister to his needs. On the other hand, they never ceased to emphasize the vastness of the Creation, and to exhort man to feel awe in the presence of the immensity of the universe and humility in the contemplation of his own insignificance. Even the earth on which man lived, which to him seemed so great, was but as a mathematical point in comparison with the firmament, not to mention the empyrean, where God himself dwelt in glory. This idea, which had its roots in the determinations of Greek science,[148] was constantly reiterated in all the astronomical works of the late Middle Ages and the Renaissance. It was emphatically set forth in Alfraganus,[149] in Sacrobosco,[150] in the Margarita Philosophica,[151] and in Bartholomaeus Anglicus.[152] Caxton’s Mirrour of the World makes similar [109] statements,[153] and examples from works expounding the traditional system of cosmology could be multiplied at will.[154]
It is obvious, therefore, that when Copernicus suggested that not only the earth itself, but also its orbit about the sun, was but a point in comparison with the sphere of fixed stars, the change he introduced was merely one of degree rather than of kind. He simply made what was already infinitely small still more infinitesimal. The revolution in metaphysical thought caused by this phase of the heliocentric system, considered by itself, was probably just as inconsequential as the philosophical reaction that occurs today when astronomers add a few more million light-years to the dimensions of the sidereal universe.[155]
The real objections made against the vastly increased distance given to the fixed stars in the Copernican system, instead of being metaphysical and theological, were primarily reasonable and scientific. Sixteenth-century astronomers, working before the invention of the telescope had revealed the stars as mere points of light without sensible diameters, had assigned fairly large apparent diameters to the most conspicuous stars.[156] Consequently, when these grossly exaggerated estimates of the apparent size of the stars were combined with the tremendous [110] distance at which Copernicus placed the stellar sphere, a few simple geometrical calculations sufficed to prove that the actual dimensions of the stars must, under his hypothesis, be incredibly large—in fact, many million times those of the earth.
The old astronomy had not pictured the stars as small bodies. The usual figures given were derived from Alfraganus and made the first-magnitude stars 107 times the size of the earth; second-magnitude, 90 times; third-magnitude, 72 times; fourth-magnitude, 54 times; fifth-magnitude, 37 times; and sixth-magnitude, the smallest visible to the naked eye, 18 times as great as the earth. Nevertheless, Copernicus’ opponents could quite rightly contend that the tremendous speed assigned to the rotating sphere of fixed stars by the Ptolemaic system was just as easy to believe as the immense size of the stars which was the inevitable corollary of his heliocentric theory.
In addition to the motions of rotation and revolution which Copernicus gave to the earth, his theory necessitated another motion to account for the precession of the equinoxes and the imaginary phenomenon of trepidation, which Copernicus, in common with his immediate predecessors, accepted.[157] The rotation of the earth had replaced the diurnal rotation of the tenth sphere, or primum mobile, of the old system. For the movement of the ninth sphere, which had had as its function the accounting for the precession of the equinoxes, Copernicus substituted a uniform movement of the earth’s axis, whereby it described the surface of a cone in a period slightly less than a year, the difference being the amount of the annual precession. Besides this “motion in declination,” as he called it, he assigned two lesser motions, or librations, to the earth’s axis, to represent both the supposed trepidation—hitherto accounted for by the oscillatory movement of the eighth sphere—and an imaginary irregularity in the change in the obliquity of the [111] ecliptic.[158] Thus the ninth and tenth spheres were eliminated, and the eighth was made motionless. But the earth, on the other hand, had been given a threefold movement: rotation, revolution about the sun, and a combined progressive and wobbling movement of its axis. Two motions of the earth were difficult enough to accept, asserted Copernicus’ scientific opponents, but three placed too great a demand on one’s credulity, particularly when this novel hypothesis was not supported by any observational evidence which could not be represented quite satisfactorily by the old system.
When the adversaries of the heliocentric theory maintained that there were no existing astronomical data which could not be adequately represented and calculated by means of the old Ptolemaic system, they were absolutely right. The De revolutionibus had not been based upon any new evidence, nor had Copernicus attempted to produce any new observations to confirm his theory. He had merely taken the existing material, and, using different initial assumptions, worked out a new mathematical system for portraying the motions of the heavens. Prior to 1543 there had been only one method by which the movements of the planets could be successfully calculated. Now there were two systems in the field, and astronomers could choose between them. From the mathematical point of view there could be no question of which system was true and which false. Both were equally true, because both could be made to give, on the whole, equally satisfactory geometrical representations of all the facts hitherto discovered by astronomical observations.
Accordingly, mathematicians would quite naturally prefer to save labor by using the simpler system of Copernicus in their calculations, regardless of whether they subscribed to the physical truth of his hypothesis. Complete astronomical tables computed upon the basis set forth in the De revolutionibus soon came into general use. The first set was published in 1551 [112] by Erasmus Reinhold (1511-1553), under the title of Prutenicae Tabulae Coelestium Motum.[159] The lack of recent observations against which positions derived from older works would be checked made Reinhold’s tables only slightly more accurate than the Alfonsine tables, or those of Regiomontanus. No marked improvement in the tables of the planetary motions was possible until a much larger body of dependable observations was available. These observations were to be provided later by Tycho Brahe, whose great work, the Progymnasmata, was published posthumously by Kepler in 1602. Meanwhile, the use of Copernicus’ methods for calculating the stellar movements continued to spread, more because of their greater simplicity than because of any outstanding superiority of the tables computed by his theory.
Since both the Copernican and the Ptolemaic systems were valid mathematically, and even the bitterest opponents of the new system admitted that it would “save the phenomena,” the truth or falsity of the heliocentric hypothesis had to be decided by an appeal to other branches of science and philosophy. Physical theory, most naturally, was the first to be brought into the discussion. Here again, the answer was equivocal. Both systems involved assumptions that seemed difficult to reconcile with common sense and reason. Intelligent, unprejudiced men could justly ask themselves whether the terrific speed assigned to the heavenly spheres by the old cosmology was inherently any more improbable than the vast distance and incredible magnitude of the fixed stars implicit in the new theory. Furthermore, the mechanical difficulties in the way of making truly workable the infinitely complex assemblage of over eighty material spheres might seem no greater than those involved in accepting the threefold motion of the earth. Even among conscientious empirical scientists the choice between the two systems had to be made on the basis of probability, rather than ascertainable facts, and the balance was poised almost evenly between the two.
Consequently, each man’s final choice was bound to depend largely on the philosophical background of his thinking. Confirmed Aristotelians, as we have previously observed, would naturally align themselves on the side of the old system, for the Copernican theory contradicted nearly every postulate in Aristotle’s doctrines of simple and compound motions, and of the natural motions inherent in the four elements and the ether. In addition, there was the belief, based upon Aristotelian physics, that the earth, if it rotated, would fly apart; also that objects projected vertically in the air, or dropped from a tall tower, would be left behind, falling far to the west of their starting point. To these latter assertions, Copernicus could well retort, “What holds together the rotating heavens in the Ptolemaic theory?”[160]
Proceeding further, the partisans of the heliocentric system, drawing support from the neo-Platonic philosophy that denied Aristotle’s infallibility and elevated other ancient philosophers to positions of equal or greater prominence, attacked the validity of some of Aristotle’s basic physical doctrines, and brought forward new interpretations of others. Copernicus himself suggested that the rectilinear motions assigned to the four elements were not natural, but constrained, and that circular motions were the only natural and uniform ones. Hence, all of the motions he assigned to the earth, being uniform and circular, were not constrained, but natural.[161]
The objections based on Aristotelian physics, although carrying some force at the time, rapidly diminished in importance during the century following Copernicus. We shall have occasion to note, in the two succeeding chapters, various important discoveries which proved that certain of Aristotle’s theories were altogether false. The resultant undermining of his authority helped to eliminate some of the most formidable opposition to the general acceptance of the Copernican system.
The absence, in 1543, of any clear scientific answer to the question of the physical truth or falsity of the heliocentric universe led some to seek an answer in the words of the Scriptures. Here, again, it was possible to find whichever answer was desired. Copernicus himself was a canon in the Cathedral of Frauenburg, and his De revolutionibus was dedicated to the Pope. Many of the early supporters of the new system were loyal churchmen. The Catholic church engaged in no official opposition to the Copernican theory for more than seventy years after its promulgation. Not until 1616, in connection with the attack on Galileo, was the De revolutionibus placed on the papal “Index,” and the doctrine of the earth’s motion declared heretical. Even then Copernicus’ book was allowed, provided all passages specifically declaring the motion of the earth were altered so as to assert that this idea, though false, was introduced merely as a mathematical hypothesis for simplifying calculations.[162]
The idea that Copernicus himself had advanced his new theory merely as a mathematical device, and did not consider it physically true, had already gained considerable credit in the sixteenth century. That false impression was created by the spurious preface inserted in the De revolutionibus by Andreas Osiander, a Lutheran theologian, when he was supervising the completion of the printing of the work in 1543. This anonymous preface is headed “Ad lectorum de hypothesibus huius operis,” and states that no blame should be attached to the author for his doctrine of the earth’s motion. The astronomer cannot find the real causes of the celestial motions, and his business is merely to devise some hypothesis by which their movements can be computed geometrically. The hypothesis need not be true, or even probable, so long as the calculations based upon it agree with observations. Many details of the Ptolemaic system are physically improbable, so that a new and [115] simpler theory may well be preferred, provided that its assumptions are explicitly recognized as mathematical devices having no relation to reality.
These remarks of Osiander’s expressed very clearly the attitude of mathematicians who recognized the practical usefulness and mathematical superiority of the Copernican system, but were unwilling, because of Aristotelian or theological prejudices, to countenance the reality of the new theory. A similar position was adopted by the church authorities. So long as the spurious preface was generally accepted as representing Copernicus’ own attitude towards his work, no action was taken by the theologians. But when, in connection with Galileo’s assertions of the physical reality of the heliocentric system, the Church realized what thorough students of the De revolutionibus had already perceived—namely, that its author clearly maintained the actual existence of the motions he attributed to the earth—the action of the papal authority was invoked. The Church merely required, however, that the body of the text be altered to agree with the ideas set forth in Osiander’s spurious preface. Thus the use of the Copernican system in astronomical calculations was never proclaimed heretical; only the belief in the reality of the earth’s motions was pronounced contrary to the Christian faith.
There was never any barrier, therefore, to the adoption of the Copernican theory by the mathematicians, so long as they did not accept it as a physical truth. On this point, neither Aristotelianism nor theology stood in the way. The extreme partisans of Aristotle had always looked upon Ptolemy’s epicycles and eccentrics as geometrical devices to “save the phenomena.”[163] We have just seen how the same attitude was officially adopted by the Church in 1616.
Aristotelian philosophy, however, did not dominate the thinking of most of the mathematicians of sixteenth-century Europe. Other things being equal, they were more likely to be drawn toward neo-Platonism. Furthermore, until 1616 loyal [116] Catholics were entirely free to interpret the scriptural passages as figurative statements rather than as scientific pronouncements, and Protestants, especially in England, never lost that freedom, being unaffected by the papal ban. Therefore the neo-Platonic influence was not necessarily counteracted by the theological. There was in consequence a large group, particularly among the leading scientific thinkers, to whom the chief positive argument of the Copernicans—the greater mathematical simplicity and harmony of their system—made a definite philosophic appeal. For them, the mere fact that Copernicus’ assumptions led to a more symmetrical scheme of the celestial motions would be ample justification for his making them, and cogent evidence in favor of their probable truth.[164]
This group would also include many who had been inspired by neo-Platonism to examine and test the Aristotelian scientific dogmas by experimental methods. They would thus be inclined to use the same scientific method in seeking further evidence in support of the new astronomy. Moreover, the keen interest of the neo-Platonists in the ideas of the early Greek philosophers, taken in connection with the Renaissance notion that Copernicus was reviving the Pythagorean system of the universe, inspired speculative minds to adopt additional theories derived from the ancients and attempt to incorporate them in the new astronomy. In this way the belief in an infinite number of worlds, and in the existence of inhabitants on the stars and planets, was to become joined to the heliocentric system, although never affirmed by Copernicus himself.[165]
The picture here given of the old conceptions of the universe and of the scientific and philosophical bearings of the new Copernican theory at the time of its first announcement provides [117] the background against which to examine the progress of astronomical thought in England during the century following the publication of the De revolutionibus. First, however, a warning must be sounded against confusing the problems and methods involved in working out theories of the celestial motions with the practical procedures of astronomical observation. The assertion that the great change introduced by Copernicus consisted in transferring the center of the astronomical co-ordinates from the earth to the sun, refers only to the theories whereby he calculated the positions of the planets. For observational purposes, the center remained, and always must remain, where the observer himself is located. Astronomical instruments, today as in the sixteenth century, are designed on the basis of a geocentric universe, since the astronomer looks out upon the heavens from a position on the earth, not the sun. Likewise, the positions of the planets, though computed by the heliocentric theory, are reduced to their directions relative to the earth before being entered in the astronomical tables.
Copernicus himself takes this question up in the De revolutionibus. After showing how to calculate what the position of a planet will be in its orbit at a given moment in the future, and what the earth’s position will be at the same moment, he explains the method of comparing the two positions and thereby deriving the planet’s direction from the earth.[166] This last fact is the only one with which the practical observing astronomer is concerned.
For this reason, all sixteenth- and seventeenth-century treatises on astronomical instruments such as astrolabes, cross-staffs, or celestial globes, assumed a geocentric system because they could not do otherwise. Only in models of the solar system—useful as illustrations of planetary theories but valueless and confusing as representations of the motions as seen by the terrestrial observer—is it possible to place the center elsewhere than in the earth. In the astrolabe, it is true, the instrument-maker, [118] by interchanging the fixed and moving parts, could demonstrate the earth’s rotation as replacing that of the heavens.[167] But in no instrument designed for practical use was it ever possible to represent the earth as revolving about the sun.[168]
Therefore, no conclusions as to an author’s actual beliefs concerning the true system of the universe can be drawn from a book dealing solely with the construction and use of an astronomical instrument. All books of that sort must assume the earth as the center from which the celestial motions are to be observed. With this final caution, we may proceed to examine the English astronomical writings of the century following Copernicus’ work.
The credit for spreading a knowledge of the new Copernican astronomy among English scientists is due chiefly to Robert Recorde and John Dee. These two men were the leaders in making sound learning in the mathematical sciences readily available to a wider group of English students in the third quarter of the sixteenth century. It was Recorde, far more than any other scholar, who was responsible for first establishing in England the custom of using the vernacular tongue for learned, yet popular, scientific works.
Robert Recorde (ca. 1510-1558) was not only a profound scholar, a master of Greek and Latin, and of mathematics, astronomy, and medicine; he was also an able teacher and a skilful writer of simple, clear English prose. The series of textbooks he wrote on the various mathematical sciences were for many decades the standard works on those subjects in England.[169] His Grounde of Artes, of which the earliest known edition was printed in 1543, was the first important work in English on arithmetic. In 1551 he published the first geometry in English, entitled The pathway to knowledg. Inasmuch as Recorde planned his successive works as a series of textbooks on the mathematical sciences, his treatise on astronomy, The Castle of Knowledge, came late in the sequence, not appearing [121] until 1556.[170] Before discussing it, therefore, the three English works dealing with astronomy which immediately preceded it will be briefly considered.
In an earlier chapter we saw how, in 1543, the only works on astronomy printed in English were translations from various medieval encyclopedias. The solitary exception was John Rastell’s Interlude of the Four Elements, in which the author made an eloquent, but long unheeded, plea for the translation into English of learned works on astronomy and other sciences. So far as astronomy was concerned, his plea went unanswered until about 1550, when a translation by William Salysburye of Proclus’ Sphaera was published by Robert Wyer as a tiny octavo volume. In the prefatory epistle “To his verye louynge cosen, John Edwardes,” the translator relates the circumstances which prompted him to turn this little elementary treatise on the sphere from Linacre’s Latin into English. Edwardes had written to Salysburye, asking him to procure a textbook of astronomy in English, and in response to this request Salysburye had searched through the London bookstalls for such a work. But let him tell his own story:
I walked my selfe, rounde aboute all Poules Churche yearde, from shop to shop, enquyrynge of suche a treatyse neyther coulde I here of any that eyther wrote of this matier proposely, nor yet occasyonallye. But what trowe you dyd I than by my fayth syr, I returned backe euen the same way (but wondrynge moche at the happe) and asked agayne for the same workes in laten, wherof there were .iii. or .iiii. of sondrye Aucthoures, brought, and shewed vnto me, amonge all whiche (for the breuyte and playnes) I chose Proclus his doynge. And this a Goddes name entended I than (for the accomplysshement of your wyll) to traducte into the Englysshe tonge. But wolde God that he, whiche translated it into the Laten, [marginal note: “That was M. Thomas lynacre.”]had taken so moche paine, as for his countre sake, as to englysshe the same also Englisshe was his natyue tonge. Greke and Laten, as well knowen, where as Englysshe to me of late yeares, was wholy to lerne, the Latyn not tasted of, the Greke not once harde of, [122] whom although euen at this present I might rather and truelye with lesse reproche, denye to haue any knowledge in it at all, than to professe the perfect phrase of any of theym three. Why than shall I attempte, for any mānes pleasure, to go aboute to translate a Scyence vnknowen, out of a tonge vnknowen, in to a tonge no better knowen vnto me.[171]
But Salysburye says that he does it for the love he bears his cousin, who “does stamer some what both in the Laten tonge, and in this science also.”
Two years later a very able treatise was published by Anthony Ascham, a physician and astronomer, who apparently had studied at Cambridge under Sir John Cheke and was probably the same person as the Anthony Ascham recorded as Roger Ascham’s elder brother. The book is entitled A Lytel treatyse of Astronomy, declaryng the leape yere, and what is the cause therof, and howe to knowe saynte Mathies day for euer,[172] and is dedicated to Sir John Cheke. It is an excellent elementary work on that branch of astronomy which has to do with the determination of the calendar, and explains the problems connected with calculating the exact length of the year and adjusting the calendar accordingly. The treatise makes no mention of Copernicus, but is based wholly on the old theories, which, incidentally, were entirely adequate for the treatment of the question in the sixteenth century, for the main difficulty at that time was the lack of sufficient accurate observations for the precise determination of the precession of the equinoxes. The author says that the writing of the book was suggested in a conversation he had with a company of “many right worshipful and honest men,” and he concludes with a plea for the reformation of the calendar.
A work of a different sort, which contributed greatly toward the wider dissemination of the principles of astronomy, was Leonard Digges’s A Prognostication of Right Good effect, [123] the earliest extant edition of which was printed by Thomas Geminus in 1555.[173] Both the title-page and the text, however, indicate that this edition was a revision and augmentation of an earlier one, dated 1553.[174] This book was again revised, and much new matter added, in 1556, at which time the title was changed to A Prognostication euerlasting. The subsequent editions reprint the contents of the one of 1556, although, as we shall see in the next chapter, the 1576 edition, revised by Leonard Digges’s son Thomas, contained an important addition by the latter, describing the Copernican system and proclaiming the idea of the infinity of the universe. No less than eleven extant editions of this work are recorded in the Short-Title Catalogue, and probably several others were printed of which no copies have survived.[175]
Leonard Digges’s Prognostication euerlasting was deservedly one of the most popular works of the period, since it was by far the best of the “perpetual almanacks” issued during the last half of the sixteenth century and was filled with all sorts of useful astronomical and astrological tables and rules. It contained, for example, astrological and meteorological rules for predicting the weather (the former tabulated at great length); descriptions of various meteorological phenomena and accounts of their causes; tables for calculating the calendar [124] and the dates of the movable feasts for several years to come; the rules for bloodletting as prescribed in astrological medicine; tables of the moon’s motion; and, finally, the description of an instrument for telling the hour at any time of day or night, together with the astronomical tables necessary for its use. Of special interest in connection with our study is Digges’s short account of the Ptolemaic system of the universe, with his table of the dimensions of the planets and their orbits, based upon the traditional figures of Alfraganus. In the 1556 and later editions, large diagrams are inserted portraying various spheres which illustrate the relative sizes of the earth, the sun, the moon, and the planets.
In view of the mistaken modern tendency to regard the frequent Elizabethan statements that the sun is in the midst of the planets as vaguely referring to the Copernican theory, Leonard Digges’s comment is worth noting: “The Sunne is placed in the middle of all the Planets: most cleare and brighte, the well of pure lighte: euery yeare finishing his course. Di. 11. ad 2.”[176] The rest of his discussion, and the diagram of the Ptolemaic universe on the opposite page, make it clear that he means that there are three planets (Saturn, Jupiter, and Mars) above the sun, and three (Venus, Mercury, and the moon) below it. That is precisely what all his contemporaries usually meant when they spoke of the sun as being “in the middle.”
The English books by Salysburye, Ascham, and Leonard Digges indicated the tendency to write about astronomy in the vernacular. Nevertheless, nothing had as yet been done to meet the real need of the Englishman who was not a master of Latin—a good astronomical textbook in his native tongue. Robert Recorde, in 1556, supplied this deficiency with the publication of his Castle of Knowledge, the first comprehensive, original treatise on the elements of astronomy to be printed in English. In this work Recorde was continuing his enlightened and far-sighted policy of providing his less learned [125] countrymen with first-class textbooks in all the important mathematical sciences.
The Castle of Knowledge is a handsomely printed small folio of some three hundred pages, containing many well-designed illustrations and geometrical diagrams. The book was dedicated to Queen Mary, and had a prefatory epistle addressed to Cardinal Pole. The plan and arrangement of the work demonstrate Recorde’s skill and insight as a teacher. He particularly emphasizes the importance of the proper method and order in instruction, insisting, in the first place, that the student must be well grounded in arithmetic and geometry before attempting to learn astronomy. For this reason, Recorde expects his two earlier books, the Grounde of Artes and the Pathway to knowledg, to have been thoroughly mastered before beginning the Castle. Assuming this preparation, Recorde proceeds, in accord with his ideas of the proper order in teaching, to present the fundamental principles and concepts underlying the science of astronomy, having the student construct his own celestial sphere to assist him in grasping these basic ideas.[177]
Since the book is written in the form of a dialogue between the Master and the Scholar, the latter is frequently made to ask questions which either involve matters too complex for him to understand until he has gone farther into the subject, or lead to difficult and disputed points of astronomical theory. In all such instances, Recorde merely gives a brief, general statement of the problem, cautioning the student that any satisfactory consideration of such matters must be postponed until he has proceeded much farther in the science and acquired sufficient knowledge to enable him fully to understand and judge the points at issue. Many of the earlier questions raised by the Scholar are later answered by the Master in the last and longest of the four books of this volume, “wherein are the proofes of all that is taught before, and other diuers notable [126] conclusions annexed therto, but nothing in a manner with out demonstration and good proofe.” However, since the work is designed only as an elementary treatise, Recorde does not attempt to take up the “theoricks” of the planetary motions, but defers all questions involving this knowledge till a later treatise,[178] which was never completed, apparently, because Recorde died in 1558.[179]
In view of Recorde’s well-defined method, his basic descriptions would naturally be given in terms of the Ptolemaic system. A clear understanding of the stellar motions as they actually appear to the observer was essential to the comprehension of any of the more complex questions of the planetary movements. To convey these concepts to the beginning student, the picture of the rotating spheres surrounding the earth was obviously the most suitable and easiest to understand. In addition, it could be illustrated by the astronomical instruments of the time, such as the astrolabe and the celestial sphere.[180]
All these considerations must be borne in mind in order to appreciate the full significance of Recorde’s reference to the Copernican theory, which has often been quoted in part, but never, I believe, reprinted in full with proper reference to its context. Recorde has just finished giving the traditional mathematical proofs that the earth is located at the center of the universe, which consist in assuming the earth placed at various positions other than at the center of the sphere of the fixed stars and showing that the geometrical consequences of such assumptions do not correspond with the observations. The [127] author then turns to the question of the earth’s movement of rotation, and has the Master say, in a distinctly ironic tone:
But as for the quietnes of the earth, I neede not to spende anye tyme in proouing of it, syth that opinion is so firmelye fixed in moste mennes headdes, that they accōpt it mere madnes to bring the question in doubt. And therfore it is as muche follye to trauaile to proue that which no man denieth, as it were with great study to diswade that thinge, which no man doth couette, nother any manne alloweth: or to blame that which no manne praiseth, nother anye manne lyketh.
Schol. Yet sometime it chaunceth, that the opinion most generally receaued, is not moste true.
Master. And so doo some men iudge of this matter, for not only Eraclides Ponticus, a great Philosopher, and two great clerkes of Pythagoras schole, Philolaus and Ecphantus, were of the contrary opinion, but also Nicias Syracusius, and Aristarchus Samius, seeme with strong arguments to approue it: but the reasons are to difficulte for this firste Introduction, & therfore I wil omit them till an other time. And so will I do the reasons that Ptolemy, Theon & others doo alleage, to prooue the earthe to bee without motion: and the rather, bycause those reasons doo not proceede so demonstrablye, but they may be answered fully, of him that holdeth the contrarye. I meane, concerning circularre motion: marye direct motion out of the centre of the world, seemeth more easy to be confuted, and that by the same reasons, whiche were before alleaged for prouing the earthe to be in the middle and centre of the worlde.
Scholar. I perceaue it well: for as if the earthe were alwayes oute of the centre of the worlde, those former absurdities woulde at all tymes appeare: so if at anye tyme the earthe shoulde mooue oute of his place, those inconueniences would then appeare.
Master. That is trulye to be gathered: howe bee it, Copernicus, a man of greate learninge, of muche experience, and of wondrefull diligence in obseruation, hathe renewed the opinion of Aristarchus Samius, and affirmeth that the earthe not only moueth circularlye about his owne centre, but also may be, yea and is, continually out of the precise cētre of the world 38 hundreth thousand miles: but bicause the vnderstanding of that controuersy dependeth of profounder knowledg then in this Introduction may be vttered conueniently, I will let it passe tyll some other time.
Scholar. Nay syr in good faith, I desire not to heare such vaine phantasies, so farre againste common reason, and repugnante to the consente of all the learned multitude of Wryters, and therefore lette it passe for euer, and a daye longer.
Master. You are to yonge to be a good iudge in so great a matter: it passeth farre your learninge, and theirs also that are muche better [128] learned then you, to improue his supposition by good argumentes, and therefore you were best to condemne no thinge that you do not well vnderstand: but an other time, as I sayd, I will so declare his supposition, that you shall not only wonder to hear it, but also peraduenture be as earnest then to credite it, as you are now to condemne it.[181]
Recorde clearly shows in this passage that he believes the Aristotelian and Ptolemaic arguments against the earth’s rotation to be entirely fallacious. The wording of his promise to expound the Copernican system more fully when the student shall have reached the stage where he will be able properly to understand it, definitely indicates that he was ready to go even farther, and accept the revolution of the earth about the sun, as well as its rotation.
The passage we have just quoted also illustrates Recorde’s familiarity with the history of Greek astronomical ideas, so far as they could be known in his time. Throughout the Castle of Knowledge, in fact, the wide range of Recorde’s learning and his thorough scholarship are apparent. Not only had he read Copernicus and mastered the arguments favoring his theory, but he also knew, at first hand, the Greek texts of Proclus, Ptolemy, and the other ancient astronomical writers. At the same time, he was well acquainted with the works of the Arabians, with the medieval treatises by Sacrobosco and others, and with the best books of his own day, such as those by Peurbach, Regiomontanus, Stöffler, and Oronce Finé.
The content of Recorde’s work, however, was by no means a mere synthesis and compilation derived from books by other authors. He applied to all of his authorities rigorous tests founded on his own wide learning, mathematical skill, and keen critical intelligence. In several instances he points out errors in the Greek texts of ancient authors, such as Proclus, Strabo, and others, which embody statements contrary to fact and common sense, and then proceeds to make the obvious emendations. One example, for Proclus, will show the nature of his corrections.[182] The text states that the star Canopus, [129] which can barely be seen above the horizon at Rhodes, is “invisible” (ἀφανής) at Alexandria, which, as Recorde rightly says, is “contrary to common sense.” He therefore emends to εὐφανής, “of good appearance” (i. e., plainly visible), since Canopus actually rises several degrees above the horizon at Alexandria.[183]
Recorde also offers some interesting comments on the mistakes made by Sacrobosco and other earlier writers because of their lack of knowledge of Greek:
Nowe this may suffise for the explication of the zodiake, after whom foloweth nexte the Colures, whiche take their names in Greeke of vnperfectnes, bycause they bee neuer seene all aboue the grounde in any oblique sphere: whereby it appeareth, that good Iohn de sacro bosco was much deceaued in comparing them to the cōpassed bowing of a wild bulles tayle, as thoughe they tooke their names thereof: but men must bear with the ignorance of that time, for lack of knowledge in the Greeke tonge.[184]
Besides carefully checking the texts of his authorities, Recorde examined all their ideas critically, and pointed out their mistakes in his book. He speaks of Erasmus Reinhold as “a manne not onlye of greate learning, but also of as greate honesty in seekinge to profite all men by his trauaile, although sometime hee wanted leasure to examine some of his writinges.”[185] Recorde then uses a demonstration of Reinhold’s which illustrates the curvature of the earth by showing that the surface of the Danube River at the mid-point of its course is several miles above the straight line joining the river’s source and its mouth. He criticizes Reinhold, however, for assuming that the Danube’s course would correspond to a great circle of the earth instead of a small circle.
The intelligent attitude toward authority which Recorde exhibits in this and in his other works is of tremendous significance for English science. The first great writer on the [130] mathematical sciences in English was no rabid anti-Aristotelian, yet at the same time he insisted that no statement, whether made by Aristotle or by any other eminent writer, should ever be accepted without previously being tested by mathematical reasoning and personal observation. What he has to say concerning Ptolemy is typical:
No man can worthely praise Ptolemye, his trauell being so great, his diligence so exacte in obseruations, and conference with all nations, and all ages, and his reasonable examination of all opinions, with demonstrable confirmation of his owne assertion, yet muste you and all men take heed, that both in him and in al mennes workes, you be not abused by their autoritye, but euermore attend to their reasons, and examine them well, euer regarding more what is saide, and how it is proued, then who saieth it: for autoritie often times deceaueth many menne.[186]
Recorde’s importance as a teacher, a scholarly scientist, and a sound critic of ancient authority has already been emphasized. A word must also be said regarding his mastery of English prose, for that contributed greatly to the influence and popularity of his book. R. W. Chambers has recently pointed out the significance of Sir Thomas More and his school in the history of English prose, and shown that an uninterrupted tradition of devotional writing lay behind them and gave them the models for their simple, yet forceful and vivid, prose style.[187] Whether Recorde was directly influenced by the More circle cannot be determined,[188] but his writing shows the same [131] characteristics and was doubtless the product of the same tradition. Note the beginning of Recorde’s “Preface to the Reader,” in the Castle:
When Scipio behelde oute of the high heauens the smallenes of the earth with the kingdomes in it, he coulde no lesse but esteeme the trauaile of men moste vaine, which sustaine so muche grief with infinite daungers to get so small a corner of that lyttle balle, so that it yrked him (as he then declared) to considre the smalnes of that their kingdom, whiche men so muche did magnifie. Who soeuer therefore (by Scipions good admonishment) doth minde to auoide the name of vanitie, and wishe to attayne the name of a man, lette him contemne those trifelinge triumphes, and little esteeme that little lumpe of claye: but rather looke vpwarde to the heauens, as nature hath taught him, and not like a beaste go poring on the grounde, and lyke a scathen swine runne rootinge in the earthe. Yea let him think (as Plato with diuers other philosophers dyd trulye affirme) that for this intent were eies geuen vnto men, that they might with them beholde the heauens: whiche is the theatre of Goddes mightye power, and the chiefe spectakle of al his diuine workes. There are those visible creatures of God, by which many wise philosophers attained to the knowledg of his inuisible power. There are those straunge constellations, by whiche Iob doth prooue the mightye Maiestie and omnipotency of God. There are those pure creatures, whiche waxe not werye with laboure, nother growe olde by continuance, but are as freshe nowe in beutye and shape, as the firste daye of their creation, and as apte nowe to perfourme their course, as they were the firste hower that they began. And thoughe time wholly depend of it, yet time can not vtter anye force in it. yea thoughe all other thinges in the worlde by tyme be consumed, and euen the moste harde metals freted into drosse, yet the liquide heauens not only gouerne time it selfe, but vtterly stande cleere from all corruption of time.[189]
Professor Chambers has also called attention to the skill of More and his school in the use of dialogue, and the vivid and truly dramatic qualities to be found in their writings.[190] Recorde, as we have seen, used the dialogue method in presenting [132] his scientific treatises.[191] Many other authors of the period, when composing works on science, philosophy, or theology, did the same, the vogue of this type of writing being traceable, ultimately, to Plato. But what distinguished Recorde’s dialogue was the dramatic quality he was able to infuse into it, even though his subject would seem far from amenable to dramatic treatment. The passage on the Copernican theory is an illustration of this, and other examples might be multiplied at will.
Enough has been said of Recorde’s textbook on astronomy to show how misleading is the statement in the Cambridge History of English Literature that Francis Bacon “was the first to write an important treatise on science or philosophy in English.”[192] The Castle of Knowledge deserves to rank as the outstanding introduction to the science of astronomy published during the sixteenth century. No other book of its type, either in Latin or in one of the European vernaculars, rivals it in its combination of intelligent pedagogical method, sound scholarship, literary style, and truly scientific attitude toward ancient authorities. Its value was recognized by Recorde’s fellow countrymen, and it became the standard work on the subject, holding this place for over half a century. The copyright was jealously guarded, all transfers being entered in the Stationers’ Register, and a new edition printed as late as 1596. Recorde’s book was imitated, three years after its first publication, by William Cuningham’s Cosmographical Glasse,[193] and copies of both of these works were included in the ship’s library on Frobisher’s first voyage, in 1576.[194] The catalogue, made in 1610, of the library collected by John, Baron Lumley (1534?-1609), lists a copy of the Castle of Knowledge, along with [133] two copies of Copernicus’ De revolutionibus.[195] Furthermore, Purchas includes Recorde among the authorities he lists at the beginning of the 1614 edition of Purchas his Pilgrimage.[196]
The outstanding merit and contemporary reputation of Recorde’s excellent book on astronomy probably explain why none of the famous Latin handbooks of that science, such as Sacrobosco’s Sphaera mundi, were ever printed in English translations. Only Proclus, issued before Recorde’s work, was published in English during the sixteenth century. Yet, in the wave of scientific translation which swept over England from 1560 onwards, the best-known popular treatises on every other type of science were turned into English. The fact that the astronomical textooks were passed over may reasonably be attributed to the recognition, on the part both of the publishers and the translators, that Recorde’s Castle of Knowledge made the Englishing of any of the standard Latin treatises unnecessary. Sacrobosco’s Sphaera mundi was translated and printed in every other important European language during the sixteenth century,[197] but the only recorded English translation, that made by William Thomas about 1551,[198] was never printed.
One other point must be mentioned in connection with Recorde’s writings. The prefaces and introductions to most of his works contain glowing eulogies of the mathematical sciences, and particularly emphasize the Platonic idea that the key to the secrets of the universe is to be found in mathematics, without [134] the aid of which any certain knowledge is impossible. The preface to the Whetstone of Witte furnishes an excellent example:
. . . I maie truely saie, that if any imperfection bee in nomber, it is bicause that nomber, can scarsely nomber, the commodities of it self. For the moare that any experte man, doeth weigh in his mynde the benifites of it, the more of them shall he see to remain behinde. And so shall he well perceiue, that as nomber is infinite, so are the commodities of it as infinite. And if any thyng doe or maie exceade the whole worlde, it is nomber, whiche so farre surmounteth the measure of the worlde, that if there were infinite worldes, it would at the full cōprehend them all. This nomber also hath other prerogatiues, aboue all naturalle thynges, for neither is there certaintie in any thyng without it, nother good agremente where it wanteth. Whereof no man can doubte, that hath been accustomed in the Bookes of Plato, Aristotell, and other aunciente Philosophers, where he shall see, how thei searche all secrete knowledge and hid misteries, by the aide of nomber. For not onely the constitution of the whole worlde, dooe thei referre to nomber, but also the composition of manne, yea and the verie substaunce of the soule. Of whiche thei professe to knowe no moare, then thei cā by the benifite of nomber attaine. Furthermore, for knowledge and certaintie in any other thynge, that mannes witte can reche vnto, there is noe possibilitie without nomber. It is confessed emongeste all men, that knowe what learnyng meaneth, that besides the Mathematicalle artes, there is noe vnfallible knoweledge, excepte it bee borowed of them.[199]
Recorde’s is the earliest known discussion of the Copernican system in an English book, but later in the same year, 1556, John Feild published in Latin his Ephemeris anni 1557 currentis iuxta Copernici et Reinholdi canones . . . ad Meridianum Londoniensem . . . supputata.[200] It consisted of a revision of Reinhold’s Prutenic Tables, reduced to the position of London for the convenience of English astronomers. The work contained a Latin preface by John Dee, in which he stated that he had persuaded his friend, Feild, to compile these tables, basing them on the Copernican theory. He had done so because the old tables were no longer satisfactory, now that the work of Copernicus, Rheticus, and Reinhold had supplanted them. [135] Dee expressed the hope that the “Herculean labors” of these men had become known to the English people, but concluded by saying that this preface was not the proper place to publish the details of the new Copernican hypothesis. Clearly, therefore, Dee fully recognized the mathematical superiority of the heliocentric theory, and urged its adoption in astronomical calculation. On the other hand, there is no certainty that he ever completely accepted the physical reality of the Copernican system of the universe. We may be sure, however, that, as the leading mathematical scientist in England and the most influential teacher and adviser in that field after Recorde’s death, he did not fail to make clear to his friends and pupils the precise nature of the problems raised by the conflict between the two systems of the universe.
John Dee succeeded Recorde as the guiding spirit of the English school of mathematicians in the third quarter of the sixteenth century. Dee, certainly, was less important than Recorde so far as the vernacular tradition was concerned. Except for his part in the great English translation of Euclid, published in 1570, all of Dee’s important printed works on the mathematical sciences were in Latin. As a writer of English prose, he was inferior to his predecessor, and also to his brilliant pupil, Thomas Digges. In learning and scholarship, however, Dee was Recorde’s equal—perhaps slightly his superior. Indeed, Dee’s fame was much greater on the Continent than Recorde’s, partly because of his having written in Latin, but chiefly because of his journeys abroad and his friendship and intimate correspondence with nearly all the leading European scientists of his day. Throughout the two decades following Recorde’s death in 1558, Dee was recognized as the supreme scientific authority in England, and was special adviser to the principal English voyages of the period, beginning in 1553 with the first Muscovy venture, to which Recorde also gave scientific counsel. Dee’s later career, during which his unrestrained optimism concerning the possibilities of natural science made him the dupe of the charlatan Edward Kelley and caused him to turn his energies to alchemy and crystal [136] gazing, has tended to obscure his real merit as a scientist and his very great services to his country. Even Dee’s modern biographer has emphasized his reputation as an astrologer, alchemist, and dabbler in spiritualism, at the expense of his significant work in legitimate science.[201] One recent scholar, however, has done much to restore the proper balance and give a truer picture of the man. Professor E. G. R. Taylor, in her Tudor Geography, devotes three chapters[202] to Dee’s labors in geography and the sciences directly related thereto. She gives the following brief summary of his position and contemporary influence:
In claiming for the mathematician John Dee an important place in the history of sixteenth-century English Geography, it is sufficient to state that he numbered among his teachers and consultants the five greatest of his geographical contemporaries: Pedro Nuñez, Gemma Phrysius, Gerard Mercator, Abraham Ortelius, and Orontius Finaeus. These men were not merely his teachers and his critics, they were his chosen and close friends, although as far as Gemma Phrysius was concerned, the friendship was cut short by premature death. To establish the fact of Dee’s influence in England, it is again sufficient to state that he was the technical instructor and adviser of Richard Chancellor, Stephen Borough, William Borough, Anthony Jenkinson, Martin Frobisher, Christopher Hall, Charles Jackman, Arthur Pet, Humphrey Gilbert, Adrian Gilbert, John Davis, Walter Raleigh and probably, but not quite certainly, Francis Drake. Among the influential men who are known to have valued his learning and judgment are most of those who played a leading part in promoting the great enterprises of discovery: the Duke of Northumberland and his sons the Dudleys, Sir Henry Sidney, the Earls of Arundel, Pembroke, Lincoln, and Bedford, Sir Francis Walsingham, Sir Christopher Hatton, Sir James Crofts, Sir William Winter, and Sir William Pickering, while, in writing to Burghley, Dee could refer to himself as ‘il favorito di vostra Excellentia’. The learned men who sought his company included all those who are themselves distinguished in the annals of English Geography: Dr. Record, Leonard and Thomas Digges, William Lambard, John Stow, William Camden, William Bourne, Thomas Blundeville, Cyprian Lucar, Abraham Hartwell, Thomas Harriot, and, foremost of all, both the elder and the younger Hakluyt.[203]
To Miss Taylor’s list of Dee’s friends on the Continent, which includes only the geographers, should be added the astronomer, Tycho Brahe.[204]
As the passage quoted indicates, Dee’s great significance in English science is due to his work as teacher, adviser, and friend to most of the English mathematicians, astronomers, and geographers of his day. His published works were very few, though he lists many manuscript treatises which were never printed.[205] Whereas Recorde’s influence, throughout the century, was transmitted by his excellent textbooks in the vernacular, Dee’s was exerted through his personal advice and teaching, and passed on by the pupils he had trained. The most famous scientist among these pupils was Thomas Digges, but many amateurs sought instruction at Dee’s house at Mortlake. Among them were several of the greatest noblemen at Elizabeth’s court, for the visits recorded by Dee in his diary[206] were not always the pilgrimages of mere curiosity seekers. In Sir Edward Dyer he had a loyal friend and patron, as well as pupil. Dyer and his friend, Sir Philip Sidney, according to the manuscript life of Sidney written in 1593 by Dr. Thomas Moffet, spent some time studying chemistry together under Dee.[207]
The center of Dee’s activities was his home at Mortlake, near London, where his library, his laboratory, and his astronomical instruments were located. London, and not the universities, became the scene of scientific study and scholarship [138] in this period. W. H. Woodward maintains[208] that the quality of scholarship in the universities declined after 1550, particularly with respect to the mathematical sciences. This is undoubtedly true, but he gives a distorted impression when he infers that English scientific learning sank to a low state in the latter half of the sixteenth century. Throughout this period groups of able scientists were actively carrying on their work outside the universities. As a consequence, the progress of English science was in no way impeded; instead, its development was promoted by its being directed toward practical rather than purely theoretical ends, and by its being brought into closer contact with the technical arts so essential in devising the instruments upon which most advances in experimental science have been based.
During the third quarter of the century, John Dee and his friends and pupils constituted the scientific academy of England. Through Dee’s intimate acquaintance and correspondence with all the most eminent scientists on the Continent, the English group was kept in constant touch with all the latest ideas and discoveries originating abroad. Dee’s unheeded plea to Queen Mary that the ancient books and manuscripts dispersed with the destruction of the monasteries be recovered, in order to found therewith a great National Library, is well known.[209] When he perceived that nothing was going to come of this suggestion, he set about forming his own library of scientific books and manuscripts, which, by 1583, had grown to over four thousand volumes. It was undoubtedly the greatest scientific library in England, and probably not surpassed in Europe, for Dee not only had collected a vast store of important medieval manuscripts on science (which he could get the more readily because they were little valued by the plunderers of the monastic houses), but he had also seen to it that all the latest printed works on the mathematical sciences should be found on his shelves.[210]
This great library was always at the disposal of Dee’s fellow scientists among his friends and pupils. If one believes that the first essential and the true center of any university is its library, Dee’s circle might truly be termed the scientific university of England during the period from about 1560 to 1583. Mention may be made, in passing, of the presence of two copies of Copernicus’ De revolutionibus on Dee’s shelves, along with the works of Nicholas of Cusa and the first Greek edition of Ptolemy’s Almagest.
Dee also realized the importance of the technical arts in scientific work and their value in developing and perfecting new and better instruments for scientific experiment and observation. Working with Richard Chancellor, who was an expert mechanician as well as a scholar, he constructed a number of astronomical instruments with specially devised transverse divisions on the scale, so as to make possible finer and more accurate readings. His most prized instrument was a huge radius astronomicus or cross-staff, ten feet long, “having the staff and cross very curiously divided into parts equall, after Richard Chancellour’s Quadrante-manner. The great instrument was in such a frame placed and layd, that it might most easily be weilded of any man to any position for practise in heavenly observation or mensurations on earth.”[211]
The position of Recorde and Dee as the outstanding and most influential English scientists at the beginning of the second half of the sixteenth century was universally conceded by their contemporaries among their countrymen.[212] Consequently, their [140] support of the Copernican theory has a special significance in the history of English astronomy. Recorde’s favorable notice of the new system, for example, would carry far more weight among later mathematicians than William Cuningham’s silence on the question. The first two books of the Cosmographical Glasse attempt to cover the same ground as the Castle of Knowledge, whereas the last two deal with geography, which Recorde had promised to treat in another book. Cuningham frequently recommends Recorde’s works to his students,[213] and the section of his volume which deals with astronomy is so obviously modeled on the Castle that it seems probable that it was the venture of a rival publisher, to compete with Recorde’s work.[214] It slightly surpasses the Castle in beauty of printing and in profusion of excellent diagrams, but is otherwise decidedly inferior—inferior to exactly the extent that Cuningham’s knowledge and scholarship fell short of Recorde’s. The Cosmographical Glasse, in fact, is merely a very able compilation from the works of generally accepted authorities, without any attempt to criticize their statements even where Recorde had already pointed out obvious errors. Cuningham goes so far as to imitate Recorde’s habit of referring to Greek texts but, instead of doing so for the purpose of making corrections, he merely gives the definitions of the chief astronomical terms, first in the Greek of Ptolemy or Proclus, then in the [141] current Latin translation of those authors, and, finally, in his own English translation.
It is an excellent commentary on the intelligent judgment of sixteenth-century astronomical workers in England that Recorde’s Castle of Knowledge retained its popularity, and was reprinted and often referred to, whereas Cuningham’s very similar volume gradually lost favor and was forgotten. The Cosmographical Glasse, incidentally, was not listed in the Lumley library, nor did its author appear among Purchas’ authorities.[215]
Another work of this period containing astronomical material of some interest is Martin Cortes’ Breve Compendio de la Sphera y de la Arte de navegar, first published at Cádiz in 1551, and translated into English in 1561 by Richard Eden, a pupil of Thomas Smith and friend of John Dee. The expense of the translation was borne by the Muscovy Company, which wished to make available in English for the use of their pilots the book that was admittedly the best modern treatise on navigation.[216] The work, published as The Arte of Nauigation,[217] went through numerous editions. Its opening chapters are really an elementary astronomical treatise based upon the traditional system, with special emphasis on the hierarchies of celestial spirits. Nevertheless, mention is made of the “Pythagorean system” in which the earth moved, because the Spanish author felt called upon to refute it by the usual Aristotelian arguments.[218] The English seamen, therefore, were made acquainted with the existence of other systems of the universe than the Ptolemaic, if they had not already acquired this knowledge from some other source.
In the preceding chapter we have seen that most of the arguments against the Copernican system were derived from the physical doctrines of Aristotle, and that, as his theories [142] in natural philosophy were attacked and disproved, the source of the most formidable opposition to the adoption of the new astronomy was being progressively weakened. Once Aristotle’s fallibility was conceded, his authority could no longer be used successfully to silence the adversaries of the formerly accepted postulates of science. The attacks upon Aristotelian physics, therefore, have a special bearing on our subject. The popular notion that the overthrowing of Aristotle’s mechanics was the single-handed achievement of Galileo at the beginning of the seventeenth century is utterly contradicted by the facts. Many of Aristotle’s doctrines had been opposed by Roger Bacon in the thirteenth century, while throughout the fourteenth and fifteenth centuries the Aristotelian physics was constantly being subjected to attack by independent scientific writers, such as Nicholas Oresme, Jean Buridan, William of Ockham, Albert of Saxony, Richard Swineshead or Suiseth, and Nicholas of Cusa.[219] Two of these men, it may be noted, were Englishmen.
In the early sixteenth century much important work was being done toward refuting Aristotle and laying the foundations for a true science of mechanics. Nicolò Tartaglia (1505-1557) greatly advanced the theory of projectiles, and Giovanni Battista Benedetti (1530-1590) wrote his Diversarum speculationum mathematicarum et physicarum liber (Turin, 1585) for the express purpose of disproving several of Aristotle’s theorems in mechanics.[220] Many years before the publication of this book, John Dee was fully acquainted with Benedetti’s ideas and experiments, and apparently had accepted and confirmed his conclusions. Dee says, in his “Mathematical Preface” to the first English translation of Euclid in 1570, after listing six principal conclusions out of Archimedes’ demonstrations relating to hydrostatics:
[143]By these verities, great Errors may be reformed, in Opinion of the Naturall Motion of thinges, Light and Heauy. Which errors, are in Naturall Philosophie (almost) of all mē allowed: to much trusting to Authority: and false Suppositions. As, Of any two bodyes, the heauyer, to moue downward faster then the lighter. This error, is not first by me, Noted: but by one Iohn Baptist de Benedictis. The chief of his propositions, is this: which seemeth a Paradox.
If there be two bodyes of one forme, and of one kynde, aequall in quantitie or vnaequall, they will moue by aequall space, in aequall tyme: So that both theyr mouynges be in ayre, or both in water: or in any one Middle.[221]
During the mid-sixteenth century Peter Ramus was the most notorious opponent of Aristotle and Aristotelianism in academic circles. He first attracted attention in 1536 by defending, in his master’s examination at the University of Paris, the sensational thesis: “All that Aristotle has said is false.” The earlier part of Ramus’ career was devoted to the reform of scholastic logic. His treatises on the sciences were not published until the latter part of his life—most of them within the decade preceding his death in the massacre of St. Bartholomew’s Day.[222] These works were designed by Ramus as a series of textbooks on the sciences making up the higher studies of the quadrivium. In the second book of his Prooemium mathematicum (1567), reprinted at the beginning of his Scholarum mathematicarum liber xxxi (1569), he deals with the applications of mathematics to astronomy. Here occurs the passage which, after praising Copernicus, pleads for a new science of astronomy which should discard all hypotheses and be founded entirely upon careful observations, developed by logic and mathematics.[223] Ramus was apparently objecting to [144] the fact that Copernicus had used combinations of eccentric circles and epicycles, just as Ptolemy had done, and thus was still retaining the old assumption that the planets must move in paths which were either circles or the result of some combination of circular motions. Ramus sought to have all preconceived notions as to the shape of the planetary orbits completely abandoned, and a new attempt made to ascertain what kind of orbit would satisfy a large number of observed positions of a planet. This was actually done some forty years later by Kepler, after Tycho Brahe had collected the body of accurate observations which made such an achievement possible. On the back of the title-page of his De motibus stellae Martis (1609), Kepler proudly proclaimed that if Ramus were still alive he would claim the reward that the French scholar had offered to the man who should produce an “astronomy without hypotheses”—namely, the surrender of his professorship at the Collège de France.
The Ramist attack, directed against both the dialectics and the scientific theories of Aristotle, played its part in weakening the latter’s authority in the eyes of the learned men of Europe. In England the scientific treatises of Ramus became well known after 1575, when they were involved in the controversy that raged over his philosophy at Cambridge University. This controversy will be further dealt with in the next chapter. It will suffice, for the present, to note that the intemperate and sweeping assault on all ancient authorities which was characteristic of some of the Ramists was not in harmony with the more reasonable and judicious attitude typical of the leading English scientists of the sixteenth century. The guiding purpose of the English investigators was to examine and test all the traditional theories and retain only those that proved to be valid. By this procedure they would avoid sacrificing what was valuable in earlier science and provide a broader foundation upon which to build for further progress. Men like Recorde, Dee, and the latter’s pupil, Thomas Digges, were all far abler and more learned in the mathematical sciences than Ramus, who did not turn to advanced mathematical studies until late [145] in life, in order to apply his new method of logic to the revision of the studies of the quadrivium. He himself tells us that until about 1559 he had been unable to get beyond the tenth book of Euclid.[224] Consequently, Ramus’ work in the sciences was directed more toward reform of pedagogical methods and to speculative and rather indiscriminate criticisms of older ideas, than to making any genuine contribution to scientific knowledge.
Throughout the sixteenth and early seventeenth centuries the sounder attitude and better-grounded knowledge of the leading English mathematicians continued to dominate English science.[225] The idea of casting aside all the accumulated learning of the past in order to create a new science of nature from the very beginnings would have seemed just as ridiculous to these men as the contention that the doctrines of Aristotle and the ancients should not be freely questioned, and as freely rejected if they failed to agree with the observed facts. The influence of the Ramists in scholastic circles, however, undoubtedly prepared the way for the more rapid acceptance of new discoveries which contradicted the Aristotelian theories.
In preparing English minds for the rejection of Aristotle’s scientific doctrines, the Zodiacus vitae of Marcellus Palingenius Stellatus played a very significant part. We have already mentioned briefly this extremely popular little book, first printed at Venice about 1531.[226] In England no other Latin poem of the Renaissance, except perhaps the eclogues of Mantuan, was so well known or so universally admired. The earliest extant Latin edition printed in England was issued by Henry Bynneman in 1572, but before that the poem had been reprinted many times on the Continent, at Venice, Basle, Lyons, and Paris, and these editions had found their way into England in great numbers. As early as 1560 an English translation, by [146] Barnaby Googe, of the first three books was published. A new edition, containing the first six books, appeared in 1561, and in 1565 Googe’s translation of the entire poem was printed by Henry Denham for Raufe Newberye under the title of The Zodiake of life. New editions of Googe’s translation were published in 1576 and 1588. Latin editions of the Zodiacus vitae printed in England were numerous after 1572, and on March 5, 1620, the book was entered as part of the English stock of the Stationers’ Company.
Additional evidence of the popularity of this poem is to be found in the fact that Palingenius was prescribed as a textbook in many of the grammar schools of the period. Foster Watson, in The Zodiacus Vitae of Marcellus Palingenius Stellatus: An Old School-Book (London, 1908), lists the schools of the time in which this poem is known to have been required reading, and discusses the nature and influence of this famous work. We may add that, in the inventory of the books of one Edwarde Beaumounte, a Bachelor of Arts at Oxford who died in 1552, the Zodiacus vitae of Palingenius appears along with Tunstall’s arithmetic and the works of the better known classical authors.[227]
The many references to Palingenius in Elizabethan literature,[228] together with the fact that most schoolboys had been required to study it and that many unlearned Englishmen had read it in Googe’s popular translation, prove that his influence on contemporary thought must have been very great. Like most long poems of the Renaissance, the Zodiacus vitae was intended by its author as a summary of all learning, and a wide variety of philosophic and scientific ideas of the past were introduced and discussed. Palingenius was an ardent neo-Platonist, and it is the neo-Platonic conception of the universe that he presents. His astronomical theories are set forth chiefly in the eleventh book of the Zodiacus vitae, entitled [147] “Aquarius,” although many important ideas on the subject are found in other books, especially “Libra” and “Pisces.” The earth is placed immovable in the center of the universe, with the changeable realm of the four elements, where everything is subject to death and decay, lying between the earth and the moon’s sphere. Beyond, or above the moon, lie the changeless, ethereal regions, through which the planets move in their orbits. But Palingenius introduces a number of ideas derived from the pre-Socratic philosophers, so that the poem is filled with scraps of information about their speculations. In connection with these ideas, the author on many occasions vigorously attacks the infallibility of Aristotle, and proclaims the necessity of examining every theory in the light of reason:
Whatsoeuer Aristotle saith, or any of them all,
I passe not for: since from the truth they many times doe fall.
Oft prudent, graue, and famous men, in errors chance to slide,
And many wittes with them deceiue when they themselues go wide:
Examples only serue, so much must errors folowed bee,
Let no man iudge me arrogant, for reason ruleth mee,
She faithfull guide of wisemen is: let him that seekes to finde
The truth, loue hir, and followe hir with all his might, and minde.[229]
Palingenius, although conceiving the stars to be attached to the eighth sphere, maintains that they are innumerable, that they are not of the same size (many of them being too small to be seen), and that the stars are many times the size of the earth. He also mentions, in passing, the idea of certain early Greek philosophers, especially Anaxagoras, Democritus, and Leucippus,[230] that every star was a world, and our earth merely one of the stars, and states:
. . . some have thought yt euery starre a worlde we well may call,
The earth they count a darkned starre, whereas the least of all.[231]
When he comes to consider what lies beyond the eighth sphere and the primum mobile, Palingenius adopts the neo-Platonic idea of a finite, spherical world, surrounded by infinite space filled only with the purest light and inhabited by the highest orders of spirits—an idea that has its source, as we have seen,[232] in the old Philolaic belief in the “outer fire”:
A sorte there are that do suppose, the end of euery thing
Aboue the heauens to consist, and farther not to spring,
So that beyond them nothing is: and that aboue the Skies
Hath Nature neuer powre to clime, but there amazed lyes.
Which vnto me appeareth false: and reason doth me teach,
For if the ende of all be there, where Skies no farther reach
Why hath not God created more? because he had not skill
How more to make, his cunning staied and broken of his will?
Or for because he had not power? but trueth both these denies,
For powre of God hath neuer end, nor bounds his knowledge ties.
. . . . . . . . . .
But learned Aristotle sayth there can no body bee,
But that it must of boundes consist: to this do I agree,
Because aboue the Skies no kinde of body we do place,
But light most pure, of bodye voyde, such light as doth deface
And farre excell our shining Sunne, such light as comprehend
Our eyes cannot, and endlesse light that God doth from him send,
Wherein together with their King the Sprites that are more hie
Doe well, the meaner sorte beneath in skies doe alwaies lie.[233]
The last quotation indicates that Palingenius makes use of the conception of the universe as inhabited by a hierarchy of spirits. Elsewhere in the poem, he is even more precise on this point, saying that the spirits inhabiting the realms of air and fire below the moon live long lives but die in the end, whereas “they that passe their life in starres, and in the purest skye, doe neuer dye.”[234] In many places throughout his poem Palingenius repeats the idea that
. . . creatures doth the Skies containe, and euery Starre beside
Be heauenly townes & seates of saincts, where Kings & Commons bide,
But perfect Kings and people eke, all things are perfect there.[235]
Although this most popular astronomical poem of the English Renaissance presents, on the whole, the conventional cosmology, it is significant that the points in which it varies from the traditional ideas came to be vitally connected with the movement toward the new astronomy of Copernicus and his successors. First among these points was its attack on the infallibility of Aristotle and the extolling of reason, not authority, as the sure guide in natural philosophy; second was the part the Zodiacus vitae played in the wider dissemination of cosmological ideas contrary to the accepted system; and third was the prominence it gave to neo-Platonic ideas and particularly to the notion that the stars were inhabited, albeit by creatures of a higher order than the mortal beings on our earth.
Religious objections to Aristotle’s cosmological theories also had their share in weakening the hold of the Greek philosopher’s ideas upon the minds of Renaissance Englishmen. The theological adversaries of Aristotle usually advanced as their authorities the words of the Bible, and the writings of the early Church Fathers and the ancient neo-Platonists. The main purpose of their attacks, as we have already noted, was to demolish the idea of the eternity of the world, and to prove that the world had a beginning in the Creation and was destined to be destroyed. Most of the religious treatises published during the latter half of the sixteenth century, and particularly those by Protestant writers, devoted from one paragraph to several chapters to proving that the world was not eternal.[236] Though far from scientific in spirit, and in other [150] respects supporting the old cosmology, these books created an attitude which made men more readily disposed to accept scientific evidence against the ancient theory of the changeless heavens.
The conflict between Aristotle’s De Caelo and the Christian doctrines of the Creation and the Last Judgment caused many writers to assign to Plato a position far superior to Aristotle among the philosophers of antiquity. An interesting illustration of this tendency is found in the short biographies of the two Greek thinkers given in the dictionary of proper names at the end of Thomas Cooper’s Thesaurus Linguae Romanae & Britannicae,[237] the great Latin-English dictionary of the Elizabethan age. Aristotle is allotted a relatively brief and perfunctory notice. The account of Plato, on the other hand, is much longer, and filled with unadulterated praise. Plato is “the prynce of all philosophers (in wysedom, knowledge, vertue, and eloquence, farre exceedyng all other Gentyles).” The compiler says: “He is called diuinus Plato, for his excellente doctrine, whiche conteineth many thinges (as sainct Augustine saieth) whiche accorde with holy scripture.”
Theological writers, however, were not the only ones in this period who were fond of quoting Plato and inclined to place him above his distinguished pupil. Platonic ideas were even more prevalent and influential among the scientists. Plato’s statements, in the seventh book of the Republic, that geometry is the knowledge of that which is everlasting and is productive of philosophic understanding, and his order that those in his ideal city must not omit the study of geometry, were cited time and again in treatises on natural philosophy.[238] Similarly, the [151] Pythagorean idea, developed in the Timaeus, that the world is made of numbers—that is, of geometrical units—became one of the most influential features of Renaissance neo-Platonism, and provided contemporary scientists with a philosophical justification for their efforts to interpret natural phenomena in terms of exact mathematical laws. A typical statement of this idea is found in John Dee’s preface to the first English translation of Euclid, where the following quotation is given, and attributed by Dee to Boethius:
All thinges (which from the very first originall being of thinges, haue bene framed and made) do appeare to be Formed by reason of Numbers. For this was the principall example or patterne in the minde of the Creator.[239]
Dee’s preface to Henry Billingsley’s translation of Euclid, in fact, contains the most forceful presentation of those aspects of Platonic philosophy which profoundly influenced the thinking of the mathematical scientists of the day.[240] This preface, which Dee dates, “Written at my poore House At Mortlake. Anno. 1570. Februarij, 9,” was, he tells us, hurriedly composed under constant pressure from the printer to complete it so as not to hold up the publication of the book. The preface is really an outline of all the branches of mathematical science, giving their nature, their relation to one another, their present state of advancement, and the chief desiderata for future progress. In short, it is a treatise on the “proficience and advancement” of scientific learning, written nearly thirty-five years before Francis Bacon’s English work, and fifty-three years before the publication of the latter’s larger Latin book, the De Dignitate et Augmentis Scientiarum. Though more restricted in scope, Dee’s work exhibits the same tendency to schematic arrangement that was characteristic of Bacon’s, but its contents [152] are of much greater scientific value, because it was written by a man who was really a scientist and actually familiar, not only with the existing state of knowledge in this field, but also with the lines upon which further research might most profitably be undertaken.
A modern reprint of this unduly neglected treatise is very greatly needed. For our present purpose, however, we must restrict ourselves to pointing out two facts: first, that Dee’s philosophy of the method of science is in its essentials based on that outlined by Plato; and second, that Dee had a clear understanding of what we mean today by the experimental method—that is, the continual alternation between the collection of data by observation, the mathematical elaboration of these data, and the devising of new experiments to check the validity of the theories deduced mathematically as probable consequences of the original observations.
In connection with the Platonic sources of Dee’s conceptions of science, we have already noted two pertinent passages in his preface to the English Euclid.[241] We may go farther, and mention his discussion of the “triple diuersitie” of “all thinges which are, & haue beyng.”[242] Dee divides them into supernatural, mathematical, and natural. His things supernatural are “immateriall, simple, indiuisible, incorruptible, & vnchangeable . . . of the minde onely, comprehended”—in other words, Plato’s “ideas.” Things natural, on the other hand, are “materiall, compounded, diusible, corruptible, and chaungeable . . . of the sense exterior . . . hable to be perceiued.” “In thinges Naturall, probabilitie and coniecture hath place: But in things Supernaturall, chief demōstration, & most sure Science is to be had.” Things mathematical are intermediate between the two, immaterial, yet by “materiall things hable somewhat to be signified.”
[153]A meruaylous newtralitie haue these thinges Mathematicall, and also a straunge participatiō betwene thinges supernaturall, immortall, intellectual, simple and indiuisible: and thynges naturall, mortall, sensible, compounded and diuisible. Probabilitie and sensible profe, may well serue in thinges naturall: and is commendable: In Mathematicall reasoninges, a probable Argument, is nothyng regarded: nor yet the testimony of sense, any whit credited: But onely a perfect demonstration, of truthes certaine, necessary, and inuincible: vniuersally and necessaryly concluded: is allowed as sufficient for an Argument exactly and purely Mathematical.
A comparison of the ideas which Dee proclaims with those set forth in Plato’s works reveals many striking similarities.[243] Dee’s references to Plato’s Epinomis and to Pico della Mirandola are also significant in this connection.[244]
To experimental science, as we understand the term, Dee gives the name “Archemastrie.” His explanation of this term, incidentally, shows his clear realization of the interdependence of all the sciences:
This Arte, teacheth to bryng to actuall experience sensible, all worthy conclusions by all the Artes Mathematicall purposed, & by true Naturall Philosophie concluded: & both addeth to them a farder scope, in the termes of the same Artes, & also by hys propre Method, and in peculier termes, procedeth, with helpe of the foresayd Artes, to the performance of complet Experiēces, which of no particular Art, are hable (Formally) to be challenged. . . . And bycause it procedeth by Experiences, and searcheth forth the causes of Conclusions, by Experiences: and also putteth the Conclusions them selues, in Experience, it is named of some, Scientia Experimentalis. The Experimentall Science. Nicolaus Cusanus termeth it so, in hys Experimentes Statikall, And an other Philosopher, of this land Natiue [Marginal note: “R. B.”; i.e., Roger Bacon] (the floure of whose worthy fame, can neuer dye nor wither) did write thereof largely, at the request of Clement the sixt. The Arte carrieth with it, a wonderfull Credit: By reason, it certefieth, sensibly, fully, and completely to the vtmost power of Nature, and Arte. This Arte, certifieth by Experience complete and absolute: and other Artes, with their Argumentes, and Demonstrations, persuade: and in wordes, proue very well their Conclusions.* But wordes, and Argumentes, are no sensible certifying: [154] nor the full and finall frute of Sciences practisable. [A hand in the margin points to this sentence, calling particular attention to it.] And though some Artes, haue in them, Experiences, yet they are not complete, and brought to the vttermost they may be stretched vnto, and applyed sensibly. As for example: the Naturall Philosopher disputeth and maketh goodly shew of reason: And the Astronomer, and the Opticall Mechanicien, put some thynges in Experience: but neither, all, that they may: nor yet sufficiently, and to the vtmost, those, which they do. There, then, the Archemaster steppeth in, and leadeth forth on, the Experiences, by order of his doctrine Experimentall, to the chief and finall power of Naturall and Mathematicall Artes.[245]
Some two years after the publication of the English Euclid, one of the most important events in the history of astronomy occurred. This was the sudden appearance, in November of 1572, of a super-nova in the constellation of Cassiopeia, which, when it first burst forth, shone brighter than Venus at its maximum brilliance, then gradually died out until, nearly seventeen months later, it became once more invisible to the naked eye. The research and discoveries in connection with this famous new star did more than anything else to bring about the downfall of the Aristotelian cosmology. According to Aristotle such a phenomenon could only appear below the moon, in the sphere assigned to the element of fire, or in the upper regions of the air. The realm above the moon was eternally changeless and no new object could appear in that ethereal region. But the one fact that was indisputably proved by contemporary astronomers was that this new star was located far above the moon’s sphere. Observations conducted throughout the months during which this star shone in the sky failed to reveal any perceptible parallax. Indeed, such research showed not only that the star must be beyond the moon, but also that it was beyond Saturn and in the firmament itself. Even the casual observer who followed it through the seventeen months during which it was visible could see that its position remained unaltered with respect to the other fixed stars.
The appearance of this star did not, of course, mark the first occasion on which Aristotle’s doctrine of the changeless heavens had been questioned. Ancient writers had placed comets above the moon and assigned regular courses to certain of them. Fredericus Nausea’s book on comets, published in Germany in 1531 and translated into English in 1577 by Abraham Fleming, mentioned the opinion of the “Pythagorists” that comets were not temporary, but perpetual, stars, having a regular course to run, as other stars have their revolution and circular motion.[246] In fact, as we have already shown, Aristotle’s theories were being constantly attacked by the scientists in the sixteenth century, and the idea of his infallibility was no longer maintained except by a few of the most bigoted of his followers. The nova of 1572, however, provided a most spectacular occasion for the refutation of one of Aristotle’s fundamental postulates, and insured the widest possible publicity for this particular demonstration of the error of his doctrine.
Certain consequences, also, followed of necessity from the proof that the new star was in the ethereal region, and helped to complete the destruction of the fundamental basis of Aristotle’s cosmological theories. First of all, if the heavens were subject to change and decay they must be constituted of matter not dissimilar to that of the terrestrial world, instead of the entirely distinct fifth element that Aristotle postulated. Furthermore, the idea of solid orbs had to be wholly abandoned. John Dee even suggested, as an explanation of the new star’s gradual disappearance, that it was moving away from the earth in a straight line.[247] Comets with their orbits lying above the moon would obviously have to pass through the various celestial spheres. The comet of 1577, five years later, gave astronomers the opportunity to secure added proof of the falsity of Aristotle’s physical theories.
Among the leaders in the research on the new star of 1572 were John Dee and his pupil, Thomas Digges. In fact, they [156] ranked next to Tycho Brahe in the importance of their contributions. Dee published, in March, 1573, a little book of trigonometric theorems for determining stellar parallax, entitled Parallaticae Commentationis Praxeosque Nucleus quidam.[248] A longer work on this new star is listed by Dee among his unpublished manuscripts, with the title “De Stella admiranda in Cassiopeiae Asterismo, coelitus demissa ad orbem usque Veneris, iterumque in Coeli penetralia perpendiculariter retracta. Lib. 3. A. 1573.”[249] Camden, in his Annales rerum Anglicarum, et Hibernicarum, regnante Elizabetha, ad annum salutis M.D.LXXXIX (London, 1615), speaks in the following terms of the new star and Digges’s and Dee’s researches:
I know not whether it be worth the labour to mention that which all historians of our time have recorded, to wit, that in the month of November, a new star, or if you will, a phenomenon was seen in the constellation of Cassiopeia, which (as I my self observed) in brightness excelled Jupiter in the Perigee or nearest point of the excentric and epicycle: and in the same place it continued full sixteen months, being carried about with the daily motion of the heaven.
Thomas Digges, and John Dee, Gentlemen, and Mathematicians amongst us, have learnedly proved by paralactic doctrine, that it was in the celestial, not in the elementary region: and they were of opinion that it vanished little by little in ascending. Certainly after the eighth month all men perceived it to grow less and less.[250]
Even more important than Dee’s book, however, was Thomas Digges’s Alae seu Scalae Mathematicae,[251] published at the end of February, 1573, slightly earlier than Dee’s work, and dedicated to Lord Burghley. Next to Tycho Brahe’s book on the new star of 1572, the best published observations of this star were those made by Thomas Digges and printed at the beginning of his Alae. So high was Tycho’s own opinion of Digges’s work that when, a few years later, he set out, in his Progymnasmata, to give a detailed analysis of all the books written [157] about this celestial phenomenon, he devoted over thirty pages to Digges’s treatise—nearly twice the space assigned to any other single work.[252] Judging from Digges’s own references to Richard Chancellor,[253] it seems highly probable that the instrument Digges used in making his surprisingly accurate observations was the famous ten-foot cross-staff designed by Chancellor and Dee, which has already been mentioned.[254]
Thomas Digges, apparently, had been trained from youth by John Dee. The son of the famous mathematician, Leonard Digges, he was born about 1546.[255] His father died in 1559, when Thomas was only thirteen years old. After his father’s death, he became intimately associated with John Dee, perhaps as his ward and pupil. In the preface to the Alae, Digges speaks of Dee as his “second parent” in mathematics and astronomy, saying that Dee had “sown many seeds of those most sweet sciences” in his mind during his “most tender years” and had “nurtured and increased others which previously had been sown in a most loving and faithful manner” by his father.[256] Dee, in the preface to his own book on the new star—to which Thomas Digges, incidentally, wrote an introductory epistle explaining why his own book had been printed before his master’s—speaks of Digges as, “charissimus mihi Iuuenis, Mathematicusque meus dignissimus haeres.”[257]
Thomas Digges fully justified Dee’s estimate of his ability, for by 1573, when only twenty-seven years old, he had taken his place beside Dee as one of the two leading mathematicians [158] and astronomers in England. Two years before, Digges had printed the Pantometria,[258] a work begun by his father, which he completed and augmented. This was instantly recognized as the best text in English on the practical applications of geometry to the problems of mensuration. His second book, the Alae, being in Latin, gained for him international fame, and secured him the friendship and admiration of so excellent a judge of its merits as Tycho Brahe.[259]
The main body of Digges’s book consists of new trigonometric theorems for determining stellar parallax, besides an account of his own observations of the new star.[260] Of special importance to our present inquiry, however, is the fact that in this work Digges definitely accepts the probable truth of the Copernican theory, proclaiming it far superior to the old hypothesis. From observations on this new star, he was hoping to obtain definite proof of the truth of the Copernican system. Having just described the extreme complexity and cumbrousness of the older system of the universe, with its mutually colliding epicyclic and eccentric orbs, and compared it to a man’s portrait made by taking the legs, the hands, the head, and the other members from entirely different pictures, Digges says that this senseless complexity was the principal reason that led Copernicus to propose a new system. He then continues:
This, at all events, I have determined to bring to mind; that opportunity is offered, and an especially opportune occasion, for proving whether the motion of the Earth set forth in the Copernican theory is the [159] sole reason why this star apparently is diminishing in magnitude; for, if it were thus, always decreasing towards the spring Equinox, it would be observed to be very small in its own magnitude. If, afterwards, increasing little by little towards the following June, it shall have continued in existence, it will scarcely be of the same brightness as when it first appeared, but in the autumn Equinox it will be seen of unusual magnitude and splendor. However, no cause of diversity of apparent quantities of this sort can be assigned other than that of its elongations from the earth, since not only would it be contrary to the basic principles of Physics that a star should increase or diminish in the Sky, but by the clear measures which have been set in this art, it will be perceived to be otherwise. Therefore, I have thought not only that a treatment of this subject is necessary, but also that Mathematics has rules for measuring the location, distance and magnitude of this stupendous star, and for manifesting the wonderful work of God to the whole race of mortals (who strive to understand something Celestial and lie not wholly buried in the earth); also for examining Theories and establishing the true System of the Universe, as well as for measuring most accurately the Parallaxes of Celestial Phenomena.[261]
The idea of attempting to verify, and, if necessary, to correct, the Copernican system of the universe by means of accurate astronomical observations of the new star and of other heavenly bodies is constantly reiterated in this work. In his preface Digges says:
I have perceived that the Ancients progressed in reverse order from Theories, which were clearly false, to seek after true Parallaxes and distances, when they ought rather to have proceeded in inverse order, and from Parallaxes, which have been observed and are known, they ought to have examined Theories. By this method it would be not at all difficult, if this remarkable Phenomenon should persist for a long time, to discern by exact judgment whether the Earth lies quiet and immovable in the center of the World, and whether that huge mass of moving and fixed Orbs rotates in a circle by a most rapid course in the space of 24 hours, or rather, that that immense sphere of fixed stars remains truly fixed and that apparent motion occurs only from the circular rotation of the Earth with reference to the celestial Poles themselves.[262]
In another place, he makes a special plea for co-operation [160] in securing the observations necessary to determine the true system of the universe, conceiving the task as a vast international project in which all astronomers should take part.[263] This appeal shows his keen appreciation of the chief desiderata of astronomy: a larger body of accurate observations, and the careful testing of all theories by the experimental method. It so happened that the observations upon which the next great advance was based were to be provided, not by himself, nor by any international group of scientists, but by his friend, Tycho Brahe. But Digges’s constant insistence on the experimental method showed that, while realizing the value of new and brilliant hypotheses in the advancement of science (witness his support of Copernicus), he was uncompromising in his demand that such hypotheses be put to the rigorous test of experiment and observation.
The research on the new star marked a turning point in the history of astronomy in England. The severe blow it dealt to the Aristotelian physical theories helped to remove one of the chief obstacles to the progress of the Copernican hypothesis. The way had already been prepared, in England, so that full advantage could be taken of such an opportunity. The English scholars of the early part of the century had promoted scientific learning, and the author of the first original astronomical textbook in the English tongue had given favorable notice to the heliocentric theory. His two successors as recognized leaders in mathematics and astronomy in England had likewise given their support to the new system. Digges, in particular, had definitely adopted it as the basis for further research, grounded upon sound experimental methods. Its scientific position, therefore, might now be considered as established. The next quarter of a century was to see a far wider dissemination of Copernicus’ ideas among the general public.
In his book on the new star, the Alae, Thomas Digges had not only won for himself a place beside John Dee as one of the two most eminent astronomers and mathematicians in England; he had also done great service to English science by his insistence on the experimental method. At the same time, he had become the recognized leader of the English supporters of the Copernican theory, and no one in Europe had shown greater eagerness to put the new heliocentric system to the test of observations and experiments which should either confirm it or necessitate some further modifications in Copernicus’ hypothesis. The Alae, however, had been written in Latin for an international audience. Digges’s next work was designed to make a knowledge of the essential features of the new system of the universe available to his less learned countrymen, and particularly to the skilled artisans and mechanics whose intelligent co-operation was so necessary to successful research in the sciences.
When, in 1576, the printer, Thomas Marshe, prepared to issue a new edition of Leonard Digges’s Prognostication euerlasting, Thomas Digges took advantage of this opportunity to revise his father’s work and to make some important additions. The most significant of these was a supplement describing the Copernican universe, entitled A Perfit Description of the Caelestiall Orbes according to the most aunciente doctrine of the Pythagoreans, latelye reuiued by Copernicus and by Geometricall Demonstrations approued. Besides a diagram of the heliocentric system, it gave an English translation of the principal sections of Book I of the De revolutionibus, in which the author had set forth the essential features of his new system and the chief arguments in its favor.
Digges clearly states, in his preface to the reader, the reasons [162] which prompted him to make this addition to his father’s book.[264] He was unwilling to allow the description of the universe according to the Ptolemaic theory to go unchallenged, since the new system of Copernicus was so much more logical and mathematically harmonious. He therefore “thought it conuenient together with the olde Theorick also to publish this, to the ende such noble English minds (as delight to reache aboue the baser sort of men) might not be altogether defrauded of so noble a part of Philosophy.”
The preface to Thomas Digges’s treatise on the Copernican theory also makes clear that the author was in no way deceived by the common assertion, based on Osiander’s spurious preface to the De revolutionibus, that Copernicus had put forward his hypothesis merely to simplify mathematical calculations and had not himself believed it to be physically true. Digges says:
And to the ende it might manifestly appeare that Copernicus mente not as some haue fondly excused him to deliuer these grounds of the Earthes mobility onely as Mathematicall principles, fayned & not as Philosophicall truly auerred. I haue also from him deliuered both the Philosophicall reasons by Aristotle and others produced to maintaine the Earthes stability, and also their solutions and insufficiency, wherein I cannot a litle commende the modestie of that graue Philosopher Aristotle, who seing (no doubt) the insufficiency of his owne reasons in seeking to confute the Earthes motion, vseth these words. De his explicatum est ea qua potuimus facultate howbeit his disciples haue not with like sobriety maintayned the same.[265]
The attitude toward Aristotle which Digges expresses in this passage is the one which we have already noted as typical of the ablest English scientists of the period. It is interesting, moreover, that, in his attack upon the Aristotelians who rigidly maintained their master’s infallibility in scientific matters, he quotes from the well-known work of Palingenius.[266] Digges’s [163] familiarity with the Zodiacus vitae was commented upon by Gabriel Harvey, who tells us that “M. Digges hath the whole Aquarius of Palingenius bie hart: & takes mutch delight to repeate it often.”[267] This knowledge is quite evident throughout the preface to Digges’s work. He makes a special point of Palingenius’ allusion to the early ideas of Anaxagoras and Democritus that every star was a world,[268] and reprints the poet’s lines in the following form:
Singula nonnulli credunt quoque sydera posse
Dici Orbes, TERRAMque appellant sydus opacū
Cui minimus Diuûm praesit &c.
The word “Terram” is printed in extremely large capitals, with the obvious design of calling attention to some of the startling implications of the new theory by means of the adroit use of a quotation from an author known and admired by nearly all of Digges’s fellow countrymen.
In translating the principal chapters of the first book of Copernicus’ great work, Digges followed the usual Elizabethan practice of working phrase by phrase, rather than word by word, so that the general result is an excellent piece of Elizabethan prose, which, although not an absolutely literal translation, is consistently faithful to Copernicus’ meaning.[269] When Digges varies from Copernicus, it is usually on the side of giving greater emphasis to the implied criticisms of some current cosmological ideas.[270] He also adds further evidence to support [164] Copernicus’ refutation of the Aristotelian contention that, if the earth rotated, objects dropped from a high tower would be left behind and finally hit the ground a considerable distance to the west of the tower. Digges brings forward the very pertinent experiment, which he had probably made himself, of dropping an object from the mast of a moving ship and noting that it appeared to fall to the deck in a straight line parallel to the mast. He says:
And of thinges ascēdinge and descendinge in respect of the worlde we must confesse them to haue a mixt motion of right & circulare, albeit it seeme to vs right & streight, No otherwise then if in a shippe vnder sayle a man should softly let a plūmet downe from the toppe alonge by the maste euen to the decke: This plummet passing alwayes by the streight maste, seemeth also too fall in a righte line, but beinge by discours of reason wayed his Motion is found mixt of right and circulare.[271]
By far the most important addition which Digges made to Copernicus, however, was his assertion that the heliocentric universe should be conceived as infinite, with the fixed stars located at varying distances throughout infinite space. Copernicus, as previously noted,[272] although bringing the question of the infinity of the universe into his refutation of his Aristotelian opponents, had refused to commit himself on this subject. Instead, he had retained in his diagram of the universe the finite sphere of fixed stars, merely making this sphere sufficiently large to account for the absence of any perceptible stellar parallax. Digges, however, clearly perceived that, the moment the rotation of the earth was conceded, there was no longer any necessity for picturing the stars as attached to a huge, rotating sphere at a definite distance from the earth. At the same time, Aristotle’s oft-quoted mathematical proofs of the finiteness of the universe were automatically invalidated.[273] Therefore, Digges had the courage to break completely with the older cosmologies by shattering the finite outer wall of the universe. He was the first modern astronomer of note to portray an [165] infinite, heliocentric universe, with the stars scattered at varying distances throughout infinite space.
Digges’s diagram of the universe, printed in the 1576 and in all later editions of the Prognostication euerlasting, was the representation of the new Copernican system most familiar to the average Englishman of the Renaissance.[274] It followed the plan printed in the De revolutionibus so far as the planets were concerned, but, instead of representing the sphere of the fixed stars by merely the customary circle standing for the eighth sphere, it scattered the stars out to the borders of the diagram, and inserted the legend: “This orbe of starres fixed infinitely vp extendeth hit self in altitude sphericallye, and therfore immouable; the pallace of foelicitye garnished with perpetuall shininge glorious lightes innumerable, farr excellinge our sonne both in quantitye and qualitye . . .”
In the text of his translation of Copernicus, Digges inserted the following paragraph of his own, emphasizing the same idea:
Heerein can wee neuer sufficiently admire thys wonderfull & incomprehensible huge frame of goddes woorke proponed to our senses, seinge fyrst thys baull of ye earth wherein we moue, to the common sorte seemeth greate, and yet in respecte of the Moones Orbe is very small, but compared with Orbis magnus wherein it is caried, it scarcely retayneth any sensible proportion, so merueilously is that Orbe of Annuall motion greater than this litle darcke starre wherein we liue. But that Orbus magnus beinge as is before declared but as a poynct in respect of the immēsity of that immoueable heauen, we may easily consider what litle portion of gods frame, our Elementare corruptible worlde is, but neuer sufficiently be able to admire the immensity of the Rest. Especially of that fixed Orbe garnished with lightes innumerable and reachinge vp in Sphaericall altitude without ende. Of whiche lightes Celestiall it is to bee thoughte that we onely behoulde sutch as are in the inferioure partes of the same Orbe, and as they are hygher, so seeme they of lesse and lesser quantity, euen tyll our sighte beinge not able farder to reache or conceyue, the greatest part rest by reason of their wonderfull distance inuisible vnto vs. And this may wel be thought of vs to be the gloriouse court of ye great god, whose vnsercheable worcks inuisible we may partly by these his visible cōiecture, to whose infinit power and maiesty such an infinit place surmountinge all other both in quantity and quality only is conueniente. But because the world hath so longe a tyme bin carryed with an opinion of the earths stabilitye, as the contrary cannot but be nowe very imperswasible, I haue thought good out of Copernicus also to geue a taste of the reasons philosophicall alledged for the earthes stabilitye, and their solutions, that sutch as are not able with Geometricall eyes to beehoulde the secrete perfection of Copernicus Theoricke, maye yet by these familiar, naturall reasons be induced to serche farther, and not rashly to condempne for phantasticall, so auncient doctrine reuiued, and by Copernicus so demonstratiuely approued.[275]
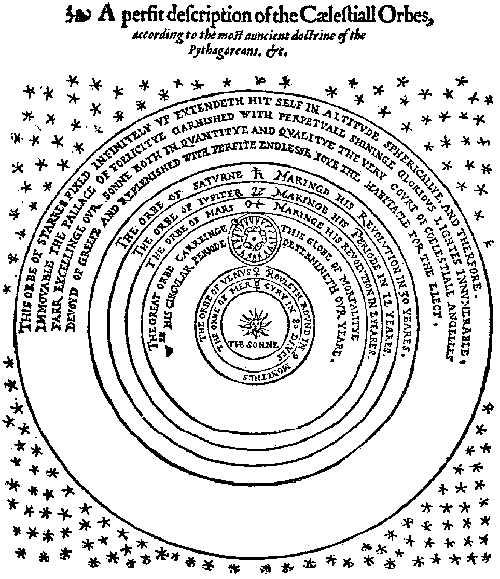
Fig. II.—Thomas Digges’s Diagram of the Infinite Copernican Universe
From A Perfit Description of the Caelestiall Orbes (1576)
It is worth noting that Digges fully realized the huge size of the stars which followed as a mathematical consequence of the Copernican hypothesis, for his legend asserts that these stars far excel the sun both in quantity and quality.[276] Furthermore, in the paragraph he added to Copernicus, he made a point of the fact that the essential merits of the new system could be fully appreciated only by the mathematicians, yet proceeded to give, out of Copernicus, the refutations of the usual arguments of the Aristotelians against the new system, even inserting, as we have observed, some additional evidence of his own against the current physical theories.
The influence of Digges’s treatise on contemporary astronomical thought can hardly be overestimated. The book in which it appeared was, as already indicated, one of the most popular works of the period. There are extant no less than seven editions containing Digges’s Perfit Description of the Caelestiall Orbes, dated 1576, 1578, 1583, 1585, 1592, 1596, and 1605. For each edition the volume was completely reprinted; there are no cases of the reissue of old sheets with a new title-page. There may well have been several other editions of which no copy has survived. In Digges’s book the average Englishman, who lacked the opportunity or the learning to read and understand Copernicus’ great work in the original, got his first authoritative exposition of the new heliocentric theory and the arguments in its favor. Digges’s reputation as one of [168] the leading mathematicians and scientists in England lent added weight to his support of the Copernican system. The manner in which he set forth his idea of the infinite universe, moreover, apparently led the majority of his countrymen to believe that the notion that the fixed stars were located at varying distances throughout infinite space was an integral part of the heliocentric hypothesis.[277]
The close association, in the English mind, of the new Copernican system and the conception of the infinity of the universe has usually been attributed to the influence of Giordano Bruno. Bruno was in England from 1583 to 1585, and the first works in which he published his speculations concerning the infinite universe were printed in England during that period. These books, however, were written in Italian, and Bruno himself spoke no English. During his sojourn in England he seems to have been known only to a limited circle, and references to his cosmological speculations in English books do not begin to appear until several years afterward.[278] Then they are based upon his later Latin works printed abroad, rather than on his Italian works printed in London.
It was Digges’s treatise proclaiming the idea of an infinite universe in conjunction with the Copernican system, and not Bruno’s speculations on this subject, that influenced the thought of sixteenth-century England. Digges, moreover, was an eminent scientist, and was eager to verify his ideas by experimental methods. Bruno, on the other hand, had arrived at his notions entirely through metaphysical speculations;[279] the Copernican theory was seized upon and incorporated in his philosophy merely because it could be made to give seeming proof, in the physical realm, of ideas already arrived at by methods in which mathematical science played no part. It is entirely possible that Digges’s brief treatise on the Copernican system first suggested [169] to Bruno’s mind the thought of using the new heliocentric theory as a physical proof of his highly speculative notions concerning the infinity of the material world. The Perfit Description of the Caelestiall Orbes had passed through at least two editions before Bruno’s arrival in England and was reprinted twice during his sojourn there, so that he had ample opportunity to know of the work and may even have met Digges himself. Edward Dyer, the friend and patron of Dee and Digges, was also a member of the Sidney-Fulke-Greville group, the circle Bruno knew in England. If a definite intermediary were to be suggested, Dyer would be the most probable person.[280]
Digges’s insistence, in his Alae seu Scalae Mathematicae, upon the need for experimental observations as a basis for determining the true structure of the universe by scientific methods, and his unwillingness to rest content with the purely metaphysical speculations of both ancient and modern philosophers, had great influence in guiding the course of English science for the next few decades. His writings directed attention to the problems raised by the conflicting cosmologies and pointed out the proper approach for investigators who desired to make some effort toward their solution. Digges gave no sanction to the tendency to fall back upon the traditional evasion of the moralists and the theologians: that such matters were improper subjects for human inquiry because it was sinfully presumptuous to attempt to discover the closely guarded secrets of the Deity.
The part that skilled artisans must play in designing and constructing new instruments and in improving various technical processes in order that further progress might be made in experimental science was fully realized by Thomas Digges, as it was by most of the leading English scientists of the sixteenth century. The translations of important scientific books and the [170] writing, in English, of sound and scholarly treatises setting forth the fundamental principles of the mathematical sciences and their many applications to practical works were parts of a patriotic program for the advancement of English science. Digges makes this motive clear in many places. His Pantometria was designed to teach the application of correct geometrical methods to difficult problems in surveying and all types of mensuration, and his Stratioticos showed the application of similar methods to military fortification and ballistics. In the dedication of the latter work to the Earl of Leicester, Digges speaks of himself as “having spent many of my yeares in reducing the Sciences Mathematicall, from Demonstratiue Contemplations, to Experimentall Actions, for the seruice of my Prince and Countrey.”[281]
In the second edition of the Pantometria (1591), Digges, speaking of another work of his then in preparation, publicly renounced further publication in Latin, saying:
And although by publishing the same my Treatize of Martiall Pyrotechnie and great Artillery in the Latin toong, I should I knowe greatlye amplifie myne owne Fame, and the admiration of such rare Mathematicians as this daye liue in seuerall Nations of Christendome, from whome I haue for farre inferior Inuentions Imprinted in my Treatize, Intituled Alae seu scalae Mathematicae, already receiued no small applause. Yet if I publish the same at all, I doe constantly resolue to doe it onely in my Natiue Language.[282]
Dee, likewise, states that the chief reason for the translation of Euclid into English was to make the whole science of geometry available to those without university training or skill in the Latin tongue, in order that they might put this knowledge to practical uses for their own good and that of the commonwealth. By the help of Euclid in their native language many students who otherwise would neglect scientific pursuits might become interested in them, and be inspired to [171] continue them, to the ultimate profit of mankind. He goes on to say:
Besides this, how many a Common Artificer, is there, in these Realmes of England and Ireland, that dealeth with Numbers, Rule, & Cumpasse: Who, with their owne Skill and experience, already had, will be hable (by these good helpes and informations) to finde out, and deuise, new workes, straunge Engines, and Instrumentes: for sundry purposes in the Common Wealth? or for priuate pleasure? and for the better maintayning of their owne estate?[283]
Many important English scientific writers of the period were men lacking a university education, who, because of the helps which scholars like Recorde, Dee, and Digges provided for them, were able to bring sound mathematical principles to the aid of their practical experience and knowledge and thus make genuine contributions and discoveries. Such men were William Bourne, the writer of many able and popular books on navigation; Robert Norman, who, in his book The New Attractive,[284] first demonstrated the dip of the magnetic needle; William Borough, comptroller of Queen Elizabeth’s navy and the author of a valuable book, A Discours of the Variation of the Cumpas;[285] and John Blagrave, the most famous designer of astronomical instruments in Elizabethan England. All of these self-educated scientists were greatly respected by men like Dee and Recorde for their genuine knowledge and achievements. Robert Norman presents with admirable directness the merited importance of the “Mechanicians” in the development of scientific learning:
But I doe verilie thinke, that notwithstanding the learned in those sciences, beeing in their studies amongst their bookes, can imagine great matters, and set downe their farre fetcht conceits, in faire shew, and with plausible wordes, wishing that all Mechanicians, were such as for want of vtterance should be forced to deliuer vnto them their knowledge and conceits, that they might flourish vppon them, & applie them [172] at their pleasures: yet there are in this land diuerse Mechanicians, that in their seuerall faculties and professions, haue the vse of those arts at their fingers ends, and can applie them to their seuerall purposes, as effectuallie, and more readilie, then those that would most condemne thē. For albeit they haue not the vse of the Greeke and Latine tongues, to search the varietie of authors in those artes, yet haue they in English for Geometrie, Euclides Elements, with absolute demonstrations: and for Arithmetike, Records workes, both his first and second part: and diuerse others, both in English, & in other vulgar languages, that haue also written of them, which bookes are sufficient to ye industrious Mechanician, to make him perfect and readie in those sciences, but especiallie to apply the same to the art or facultie which he chieflie professeth. And therefore I would wish the learned to vse modestie in publishing their conceits, & not disdainfullie to condemne men that will search out the secrets of their artes and professions, and publish the same to the behoofe & vse of others, no more then they would that others shuld iudge of them, for promising much and performing little or nothing at al. Aristotle sayth, that euerie man is best to be beleeued in his owne professed Art and Science. Now (curteous reader) I am to request thee to accept of this my discourse, wherein I haue taken some paines (as the trauaile it selfe may testifie) and bene at some charge, for the more carefull and orderlie handling of such matters as are necessarilie incident to this present treatise: All which I haue bene content to doe, that the worke (though it be not big, yet effectuall) by the common vse thereof, may yeeld profit accordingly, to them specially that are of capacitie to comprehend this new reuealed secret. To conclude, the chiefest & onely marke whereat I lay leuell, was the benefiting of my Countriemen, in whom I wish continuall increase of knowledge and cunning, as in all other commendable professions, so chieflie in those that are most necessarie and profitable.[286]
In addition to explaining his discovery of the dip of the magnetic needle, Norman, in his New Attractive,[287] discussed briefly the variations of the compass, showing that the actual observations of mariners proved that this variation was not uniform, as had been maintained by earlier writers, including Martin Cortes. William Borough, to whom Norman presented his book, penned his Discours of the Variation of the Cumpas to “be annexed to” The New Attractive, and the two works are usually found together in the same volume. Borough’s [173] treatise gives detailed instructions for the accurate mathematical determination of the variation, and records observations of his own, made on his northeastern voyages, which clearly disproved the theory that the compass needle always pointed to a certain magnetic pole. Borough often refers his readers to Copernicus’ De revolutionibus for the demonstration of certain mathematical propositions. His preface “To the Trauelers, Seamen, and Mariners of Englande” made a plea for the collection of accurate data on the variation of the compass in different parts of the world, so that the maps and sailing charts could be improved. Profound learning, according to Borough, was not essential for this task, because there were books in the English tongue “sufficient for an industrious and willyng minde to attain to greate perfection” in the necessary sciences of arithmetic, geometry, and astronomy.[288]
The practical and experimental nature of English science in the late sixteenth century cannot be too strongly emphasized, in view of the popular misconception of its character, derived largely from Bacon’s highly misleading portrayal of the aims and methods of the scientists of his day.[289] The leading scholars, such as Digges and Dee, were not interested in mere abstract theory, except in so far as it was necessary for determining fundamental principles. Like Bacon, they had a clear vision of the practical utility of science for the relief of man’s estate, and they sought the co-operation of all classes of workers in the realization of their dream, well aware of the potential value of each man’s specialized experience and technique when intelligently applied to some designated end.
In astronomical research the influence of this experimental attitude, which owed so much to the work of Thomas Digges, persisted throughout the period we are studying, although some time elapsed before we have any recorded instances of definite results. The hope which Digges had held in 1573 that the new star would afford experimental proof of the truth of [174] the Copernican system was doomed to disappointment. Although astronomers had the opportunity of observing it for over a year and a half, they were unable to detect any annual parallax for this most famous super-nova. The old dilemma consequently remained to be faced by all the sixteenth-century scientists: either they must accept the hypothesis that there was an incredibly great interval of apparently empty space between the orbit of Saturn and the nearest of the fixed stars, together with the corollary that every one of the visible stars must be many times larger than the sun; or they must reject the main features of the Copernican theory and return to Ptolemy’s cosmology or some less radical modification thereof. Digges’s treatise of 1576 on the Copernican system proved that, in spite of the failure of the new star to furnish experimental verification of the heliocentric theory, he was not only willing to choose the former alternative, but also ready to go the full length in that direction and proclaim the stellar regions to be infinite. In view of his consistent advocacy of the experimental method, one naturally wonders what reasons prompted Digges to take this course. His known descriptions of an early type of telescope instantly come to mind in this connection, together with the descriptive title he gave in 1579 for a commentary on Copernicus which he had started to write. Among the “Bookes Begon by the Author, heereafter to be published” which he lists at the time was
Commentaries vpon the Reuolutions of Copernicus, by euidente Demonstrations grounded vpon late Obseruations, to ratifye and confirme hys Theorikes and Hypothesis, wherein also Demonstratiuelie shall be discussed, whether it bee possible vpon the vulgare Thesis of the Earthes Stabilitie, to delyuer any true Theorike voyde of such irregular Motions, and other absurdities, as repugne the whole Principles of Philosophie naturall, and apparant groundes of common Reason.[290]
What these “late Obseruations” were we can only conjecture, for Digges’s treatise was probably never completed. The possibility that he had examined the heavens through a combination [175] of lenses and mirrors corresponding to our modern telescope cannot be ruled out, although definite proof may never be forthcoming.[291] Even the most casual observation of the sky with such an instrument would have provided Digges with ample experimental justification for his assertion that the stellar regions should be conceived of as infinite. His observations would have revealed to him the fact that the stars are infinitely more numerous than they seem to the naked eye. At the same time, he would have discovered that his instrument, in giving clearer definition to the stars, did not increase their apparent diameters but showed them as mere points of light. The incredible sizes of the stars as compared with our sun—a difficulty that had been one of the chief scientific objections to the Copernican theory so long as these stars were assigned diameters of from one to two minutes of arc—would no longer have to follow as an inevitable consequence of the new system, so that this very powerful argument of its opponents would have been overcome.
There are many references in Digges’s works to the marvels achieved in terrestrial observations by means of frames of lenses and mirrors, or “perspective glasses,” to use the customary Elizabethan term for them. The most detailed description occurs at the end of Chapter 21 of the first book of his Pantometria:
Thus much I thought good to open concerning the effects of a plaine Glasse, very pleasant to practise, yea most exactly seruing for the description of a plaine champion countrey. But marueilous are the conclusions that may be performed by glasses concaue and conuex of Circulare and parabolicall formes, vsing for multiplication of beames sometime the aide of Glasses transparent, which by fraction should vnite or dissipate the images or figures presented by the reflection of other. By these kinde of Glasses or rather frames of them, placed in due Angles, yee may not onely set out the proportion of an whole region, yea represent before your eye the liuely image of euery Towne, Village, &c. and that in as [176] little or great space or place as ye will prescribe, but also augment and dilate any parcell thereof, so that whereas at the first apparance an whole Towne shall present it selfe so small and compact together that yee shall not discerne anye difference of streates, yee may by application of Glasses in due proportion cause any peculiare house, or roume thereof dilate and shew it selfe in as ample forme as the whole towne first appeared, so that ye shall discerne any trifle, or reade any letter lying there open, especially if the sunne beames may come vnto it, as plainely as if you were corporally present, although it be distante from you as farre as eye can discrie: But of these conclusions I minde not here more to intreate, hauing at large in a volume by it selfe opened the miraculous effects of perspectiue glasses.[292]
The separate volume on perspective glasses, mentioned here, has apparently been lost. Among Digges’s contemporaries, however, there was a keen interest in the properties of these combinations of lenses and mirrors, and numerous references were made to their use in terrestrial observations. Dee, for example, alludes to them several times in his preface to Euclid,[293] and doubtless dealt with them at some length in several of his unpublished manuscript treatises.[294] About 1580 William Bourne, one of the ablest practical scientists of the period, wrote at Lord Burghley’s request a short treatise on the properties and qualities of glasses for optical purposes, and the [177] making, polishing, and grinding of them.[295] After discussing the method of manufacture and the properties of convex and concave mirrors and convex lenses, Bourne says, at the end of his treatise:
For that the habillity of my purse ys not able for to reache, or beare the charges, for to seeke thorowly what may bee done with these two sortes of Glasses, that ys to say, the hollowe or concave glasse: and allso that glasse, that ys grounde and polysshed rounde, and thickest on the myddle, and thynnest towardes the sydes or edges, Therefore I can say the lesse vnto the matter. For that there ys dyvers in this Lande, that can say and dothe know muche more, in thes causes, then I: and specially Mr. Dee, and allso Mr. Thomas Digges, for that by theyre Learninge, they have reade and scene many moo auctors in those causes: And allso, theyre ability ys suche, that they may the better mayntayne the charges: And also they have more leysure and better tyme to practyze those matters, which ys not possible for mee, for to knowe in a nombre of causes, that thinge that they doo knowe. But notwithstanding upon the smalle proofe and experyence those that bee but vnto small purpose, of the skylles and knowlledge of these causes, yet I am assured that the glasse that ys grounde, beynge of very cleare stuffe, and of a good largenes, and placed so, that the beame dothe come thorowe, and so reseaved into a very large concave lookinge glasse, That yt will shewe the thinge of a marvellous largeness, in a manner vncredable to bee beleeved of the common people. Wherefore yt ys to bee supposed, and allso, I am of that opinyon, that havinge dyvers, and sondry sortes of these concave lookinge glasses, made of a great largeness, That suche the beame, or forme and facyon of any thinge beeynge of greate distance, from the place, and so reseaved fyrste into one glasse: and so the beame reseaved into another of these concave glasses: and so reseaved from one glasse into another, beeynge so placed at suche a distance, that every glasse dothe make his largest beame. And so yt ys possible, that yt may bee helpped and furdered the one glasse with the other, as the concave lookinge glasse with the other grounde and polysshed glasse. That yt ys lykely yt ys true to see a smalle thinge, of very greate distance. For that the one glasse dothe rayse and enlarge, the beame of the other so wonderfully. So that those things that Mr. Thomas Digges hathe written that his father hathe done, may bee accomplisshed very well, withowte any dowbte of the matter: But that [178] the greatest impediment ys, that yow can not beholde, and see, but the smaller quantity at a tyme.[296]
Another evidence of the familiarity of the sixteenth-century English scientists with some form of an early telescope and their use of it in terrestrial observations is found in Thomas Harriot’s account of the instruments taken on the expedition to Virginia in 1585. Among others, he mentions “a perspectiue glasse whereby was shewed manie strange sightes.”[297] Yet, despite the many proofs of the existence of optical instruments quite similar to the telescope, and the references, such as William Bourne’s, to Dee and Digges as the two men most skilled in these matters, there is no clear proof that Digges or any other astronomer in England used a telescope for examining the heavens prior to the year 1609.[298] The earlier telescopes described by Digges, Dee, and Bourne seem to have been merely set up in frames, since there is no mention of an inclosing tube. But this fact would have no effect, of course, upon the evidence that would have been derived had Digges used his instrument for examining the heavens.
It seems most improbable that the idea of turning one of his frames of perspective glasses toward the sky would never have occurred to Digges during the course of his experiments. Both Digges and Dee refer to manuscripts of Roger Bacon as the principal sources of their knowledge concerning the properties of lenses and mirrors, and Bacon, in the passage describing the uses of combinations of these glasses for making distant objects appear large and close at hand, says that by their means [179] one could make the sun, moon, and stars apparently descend here below.[299] It is unlikely that Digges would have failed to follow up this suggestion if he had had the opportunity.
After about 1580, however, Digges had little chance to pursue consistently any series of astronomical or scientific investigations. Because of his ability as a military engineer he was called into the service of his country, first to supervise the fortification of Dover harbor, and later as muster-master-general of the English forces in the Netherlands. He thus had little time to devote to scientific research and writing, and none of the works he had under way in 1579 was ever completed and published. Furthermore, the lawsuits lodged by Digges against the cousin who had acted as his father’s executor, in order to recover the sums this relative had embezzled, dragged on unsuccessfully through many years.[300] Digges never had the funds, therefore, to carry on the systematic astronomical research which he had proclaimed in the Alae as so necessary for the advancement of that science. His own fortune would not permit him to establish an observatory and equip it with instruments and a staff of trained assistants. The munificence of King Frederick II in handsomely endowing Tycho Brahe’s work[301] deserves as great a share of the credit for the latter’s splendid achievements as does Tycho’s own genius. Digges never had any prospect of such a grant, for Elizabeth’s finances were always in too precarious a state for her to give any thought to subsidizing astronomical research. After 1583, even the instruments and laboratories of his friend Dee were no longer available for Digges’s use, because they had been destroyed by the mob that sacked Dee’s house at Mortlake in the fall of that year.[302]
The influence of Thomas Digges’s work on astronomical thought in England persisted for several decades, despite the [180] fact that circumstances prevented his carrying through the program of scientific research he had envisioned. He had made a knowledge of the essentials of the Copernican theory available to all his countrymen and had implanted in their minds the notion that the infinity of the universe was an integral part of the heliocentric hypothesis. He had likewise done much to further the spirit of experimental research in England, and to direct the attention of English scientists to the possibility of solving the disputed points of cosmology by means of observations based upon scientific methods. Not only had he created an interest in the technical problems connected with fashioning those combinations of lenses and mirrors out of which the telescope in its modern form was to be evolved, but he had also led his countrymen to be on the alert for new discoveries which would afford satisfactory physical reasons for the planetary motions. He had contributed his share to exploding the physical theories of Aristotle which had been offered as explanation and proof of the earth’s immobility in the center of the universe. As yet, however, no scientific physical reasons had been presented to explain what caused the earth to move in the way Copernicus supposed.
An Englishman and contemporary of Digges, William Gilbert, was the first to propose a physical explanation of the earth’s rotation, ascribing it to the earth’s magnetic properties. Although Gilbert’s experiments were begun many years earlier, his great work, the De Magnete, was not published until 1600, five years after Digges’s death. Before considering Gilbert’s book, therefore, some account should be given of the progress of astronomy in England between the time of the publication of Digges’s treatise in 1576 and the end of the sixteenth century.
From 1576 onwards, references to Copernicus become much more frequent in English books. Before this date the only important notices of the new system were confined to the works of the most eminent mathematical scientists. Thereafter, nearly every writer on astronomy felt it necessary to pay some attention to the heliocentric theory, if only to try to refute it by the conventional [181] Aristotelian arguments. The abler compilers of popular handbooks on that science usually adopted many of Copernicus’ figures, particularly those for the precession of the equinoxes, and gave due praise to his astronomical skill regardless of whether they accepted the physical reality of his system. Incidental allusions in other types of books testify to the growing knowledge of the Copernican theory among many classes of English authors.
The new cosmological ideas were not being ignored in the universities. In 1576, the very year of Thomas Digges’s treatise on the Copernican system, one of the questions assigned for disputation in Vesperies by candidates incepting as Masters of Arts at Oxford was, “An terra quiescat in medio mundi?”[303] Which side of the question was taken by the candidate and which by the proctor who responded is not indicated by the records, but we may be certain that the theories of Copernicus and the opposing doctrines of Aristotle were the chief subjects of debate. Among the questions in 1581 was, “An materia sit in caelo?” It indicates that the recent astronomical discoveries concerning the nature and location of comets and of the new star were having their repercussions in academic circles. A question argued in 1588 was, “An sint plures mundi?” The selection of such topics is evidence that the fundamental postulates of Aristotelian cosmology were regarded as live subjects for scholastic debate, regardless of which side the candidates were expected to take on the issues.
A mere enumeration of casual references to Copernicus in English books after 1576 would serve no useful purpose, but a few typical ones may be given here as indicative of the increasing knowledge of his work, and of the various attitudes toward it prevailing in England. Gabriel Harvey, in his poem in memory of Sir Thomas Smith written in 1578, mentions Copernicus and Rheticus in his summary of the world’s greatest writers on astronomy, speaking of them in the following terms:
. . . . . . . . . . . . aliosqúe recentes
Astronomos, praeterqúe alios Copernicum acutum,
Praeconemqúe eius Ioachimum Rheticum . . .[304]
The passing allusion to the new astronomy in Sir John Davies’ Orchestra or A Poeme of Dauncing[305] is notable for its favorable attitude toward the scientific basis for the idea of the earth’s motion:
Onely the Earth doth stand for euer still,
Her rocks remoue not, nor her mountaines meete,
(Although some witts enricht with Learnings skill
Say heau’n stands firme, & that the Earth doth fleete
And swiftly turneth vnderneath their feete)
Yet though the Earth is euer stedfast seene,
On her broad breast hath Dauncing euer beene.[306]
Allusions to the new astronomy occur with increasing frequency in popular handbooks on scientific subjects, although most books of this type, it is true, continued for many years to reprint little more than epitomes of the conventional ideas. Francis Shakelton, in a book describing the comet of 1580 and the evils it foretold to the individuals and nations who refused to repent and amend their ways of life, refers to the fact that astronomers had proved that some comets, and the new star of 1572, were above the moon, where nature as typified by the four elements had no power. He mentions particularly, in this connection, Digges’s book, the Alae seu Scalae Mathematicae.[307] In the philosophical encyclopedia written in French in 1575 by Louis Le Roy, and translated into English by Robert Ashley and published in 1594 with the title Of the Interchangeable Course, or Variety of Things in the Whole World,[308] [183] Copernicus is eulogized as one of the greatest of modern mathematicians, along with Regiomontanus, Peurbach, and Nicholas of Cusa.
Of even greater interest is a passage in a treatise on chemistry and medicine written by Richard Bostocke, entitled, The difference betwene the auncient Phisicke . . . and the latter Phisicke.[309] It proclaims the superiority of Paracelsian chemistry and medicine over the previous practice in those sciences. At the same time the author says, speaking of Paracelsus:
He was not the author and inuentour of this arte as the followers of the Ethnickes phisicke doe imagine, as by the former writers may appeare, no more then Wicklife, Luther, Oecolāpadius, Swinglius, Caluin, &c. were the Author and inuentors of the Gospell and religion in Christes Church, when they restored it to his puritie, according to Gods word, . . . And no more then Nicholaus Copernicus, which liued at the time of this Paracelsus, and restored to vs the place of the starres according to the trueth, as experience & true obseruatiō doth teach is to be called the author and inuentor of the motions of the starres, which long before were taught by Ptolomeus Rules Astronomicall, and Tables for Motions and Places of the starres . . .[310]
Bostocke was obviously a Copernican. The same was not true of Thomas Hill, who compiled a popular textbook of astronomy. Yet Hill inserts many of Copernicus’ figures and often refers to the heliocentric system, although he sides with the older theory and cites the usual Aristotelian reasons. Hill was probably the most prolific compiler of popular scientific handbooks during the third quarter of the sixteenth century. Little else is known about him, except that he must have died about 1575. Only two new works of his were published after that date. The first of these, if the pseudonym “Dydymus Mountaine” is meant to refer to the same Thomas Hill,[311] was entitled The Gardeners Labyrinth. This book was printed in 1577, and, in his dedication of the work to Lord Burghley, a [184] certain Henry Dethicke states that he had been responsible for perfecting and publishing it after the author’s recent death, because of a promise given his dying friend.[312]
The second work of Hill’s to be published posthumously[313] was his treatise on astronomy, entitled The Schools of Skil. This was not printed until 1599, when the deceased author’s manuscript came into the hands of William Jaggard, who, realizing that the demand for works of this sort might make its publication a profitable venture,[314] saw it through the press and offered it for sale at his shop. Jaggard’s preface, dated “April. 8. 1599,” is of considerable significance as evidence of the general interest in scientific learning in England:
Diuers haue writtē of sundry matters in former Ages, to the intent to benefit these our later times, wherin a man can name no kind of Art or Science, liberall or mechanicall, but there are as rare wits to bee found as euer liued since lerning florished. The reason is good that it should be so. For first, we haue come to our handes, vse and iudgement, whatsoeuer either antique or moderne Authors haue left behinde. Secondly, the gouernment (God be blessed) hath a long time (now these 40. yeares) bin so peaceable, that Students had neuer more libertie to looke into learning of any profession, for the inlarging of their vnderstanding. Lastly, the meanes otherwise, as well out of the vniuersities, as in them, haue been and are so many and so good, to attaine to all knowledge, that I dare be bold to say, England may compare with any Nation for number of lerned men, and for variety in professions. Of late a man of good merit, named Tho. Hill, painful with his pen whiles he liued, (as the world can witnesse, being possessed of sundry his works in Print) now deceased, left this Treatise Mathematical, intituled The Rudiments of the Sphere: which being found by iudgment of the lerned in the like profession, worthy the publishing, I haue, not only for the memory of the Author, but also for the profit of al wel affected Students, vndertaken to set forth. Therein whosoeuer bestoweth time & labor [185] to read, with a temperate and sober spirit, I doubt not but they shall be satisfied in all such points, as this Mathematician pretendeth to handle.[315]
Hill’s book has considerable merit as a textbook of the traditional astronomical ideas. Although it is mainly a compilation from the works of generally accepted authorities, without any attempt at a critical examination and sifting of their ideas, Hill has performed the compiler’s task with commendable thoroughness. The many illustrative problems he gives are well designed for training the student in the practical applications of the science. In short, the book is definitely superior to Cuningham’s Cosmographical Glasse, and the many references to Copernicus and the use of his figures[316] are indicative of the way in which the progress of the new astronomy among the ablest scholars was influencing the professional compilers of popular scientific handbooks. Hill’s brief description and rejection of the Copernican theory is worth noting:
Aristarchus Samius, which was 261 yeares, before the byrth of Christ, tooke the earth from the middle of the world, and placed it in a peculiar Orbe, included within Marses and Venus Sphere, and to bee drawne aboute by peculiar motions, about the Sunne, which hee fayned to stande in the myddle of the worlde as vnmoueable, after the manner of the fixed stars. The like argument doth that learned Copernicus, apply vnto his demonstrations. But ouerpassing such reasons, least by the newnesse of the arguments they may offend or trouble young students in the Art: wee therefore (by true knowledge of the wise) doe attribute the middle seate of the world to the earth, and appoynte it the Center of the whole, by which the risings, & settinges of the stars, the Equinoctials, the times of the increasing and decreasing of the dayes, the shadowes, and Eclipses are declared.[317]
The rapidly increasing knowledge of the new Copernican theory aroused the Aristotelians and the conservative theologians [186] to renew their attacks upon it, even though its open supporters were still largely confined to the ranks of the mathematical scientists. Typical of the religious opposition to scientific ideas was the Physica Christiana of Lambert Daneau (1530-1596), a French Protestant divine, who spent many years teaching at Geneva. This book, published at Geneva in 1576, was devoted to a lengthy exposition of the thesis that all genuine scientific knowledge was to be sought in the passages of the Scriptures and not in the works of heathen philosophers like Plato and Aristotle. The book was translated into English by Thomas Twyne, and published in 1578 as The Wonderfull Woorkmanship of the World.[318] Daneau devotes many pages to a refutation of Plato’s doctrine of “ideas,” because “the Scripture in no place maketh mention of this ideall worlde, as they call it.”[319] The doctrine of infinite worlds, held by Democritus and Epicurus, is also violently attacked.[320] Daneau is even uncertain as to whether the earth is spherical or not, since biblical passages can be quoted both for and against the idea. He finally concludes that God alone knows the truth, but that the probability is that the world is round.[321]
Another Frenchman, Guillaume Saluste Du Bartas, the author of one of the most famous poems of the Renaissance, was less narrow-minded in his attitude toward science. His poem, following the literary ideals of the time, was designed as a compendium of all knowledge and learning. La Sepmaine, ou Création du monde, first printed in complete form in Paris in 1578, gave a poetic description of the creation of the world. The poem was divided into seven parts, or “days,” which parallel the account in Genesis of the order that the Lord followed in bringing the world and its creatures into being. Du Bartas’ La Seconde Sepmaine, printed separately in 1584 and included with La Sepmaine in many later editions, was a collection of shorter poems dealing chiefly with supposed events in the early history of the world.
The popularity and influence of Du Bartas, and of Joshua Sylvester’s English translation of his works, is recognized by all students of the literature of the English Renaissance and need not be discussed here. Sylvester’s complete translation of the French poet was not published until 1605,[322] but many English editions of parts of Du Bartas had been printed before the end of the sixteenth century, and his poems were known in England from 1580 onwards. It is important, however, to realize that Du Bartas was a poet, not a scientist, and was lacking in any profound understanding of the underlying principles of astronomy or cosmology. His procedure was to take the ideas inherited from the late Middle Ages, as he found them set forth in the great encyclopedias of knowledge, and cast them in poetic form. He also borrowed freely from the ancient cosmological poets, such as Lucretius, but without any attempt to reduce to a consistent system the often conflicting theories which he embodied in his Weekes.[323] At the same time, he constantly sought to emphasize the moral and religious aspect of his material, and to make his work a sort of Christian epic. His “First Day of the First Week” opens with a bitter refutation of those “atheists” who held to Aristotle’s idea that the world was eternal, without beginning or end, or who accepted Democritus’ idea of infinite worlds.[324] His arguments here are the usual ones of the encyclopedists, derived, in turn, from the early Church Fathers. When he feels called upon to confute new ideas which disagree with his authorities, he makes little attempt to examine and to understand the reasons behind these theories, but scornfully rejects them simply because of their novelty. His method of refutation is based upon repeated assertions rather than upon any attempts at logical proof. [188] This is exactly the method he follows in discussing the Copernican theory. He gives none of the arguments favoring the Copernican system, but merely recites a list of the Aristotelian physical axioms denying the earth’s motion. These axioms, as we have already seen, were rapidly being disproved by the experimental scientists of Du Bartas’ own day. It is significant, nevertheless, that Du Bartas does not brand the Copernicans as atheists, but merely holds them up to scorn for their wilfulness in denying Aristotle’s doctrines of motion.
As the Ague-sick, upon his shivering pallet,
Delayes his health oft to delight his palat;
When wilfully his taste-less Taste delights
In things unsavory to sound appetites:
Even so, some brain-sicks live there now-adayes,
That lose themselves still in contrary wayes;
Prepostrous Wits that cannot row at ease,
On the Smooth Channell of our common Seas.
And such are those (in my conceit at least)
Those Clarks that think (think how absurd a jest)
That neither Heav’ns nor Stars do turne at all,
Nor dance about this great round Earthly Ball;
But th’ Earth itself, this Massie Globe of ours,
Turns round-about once every twice-twelve hours:
And we resemble Land-bred Novices
New brought aboord to venture on the Seas;
Who, at first lanching from the shore, suppose
The ship stands still, and that the ground it goes.
So, twinkling Tapers, that Heav’n’s Arches fill,
Equally distant should continue still.
So, never should an arrow, shot upright,
In the same place upon the shooter light;
But would doe (rather) as (at Sea) a stone
Aboord a Ship upward uprightly thrown;
Which not within-boord falls, but in the Flood
A-stern the Ship, if so the Winde be good.
So should the Fowls that take their nimble flight
From Western Marches towards Morning’s light;
And Zephyrus, that in the Summer time
Delights to visit Eurus in his clime;
And bullets thundred from the canon’s throat
(Whose roaring drowns the Heav’nly thunder’s note)
Should seem recoil: sithens the quick career,
That our round Earth should dayly gallop here,
Must needs exceed a hundred-fold (for swift)
Birds, Bullets, Windes; their wings, their force, their drift.
Arm’d with these Reasons, ’t were superfluous
T’ assaile the Reasons of Copernicus;
Who, to salve better of the Stars th’ appearance,
Unto the Earth a three-fold motion warrants:
Making the Sun the Center of this All,
Moon, Earth, and Water, in one onely Ball.
But sithence here, nor time, nor place doth sute,
His Paradox at length to prosecute;
I will proceed, grounding my next discourse
On the Heav’n’s motions, and their constant course.[325]
Sylvester’s translation, because of its popularity, helped to spread the knowledge of the Copernican theory, and may well have prompted the more curious readers to inquire further into the hypothesis which had been dismissed so summarily.[326] There were many Englishmen who, although willing to pay lip service to the idea, which Du Bartas and many others proclaimed, that man should not inquire too curiously into the mysteries of creation, were nevertheless eager to discover whatever they could concerning the true nature of the universe.[327]
Du Bartas’ popular poem upheld the physical theories of Aristotle against the moderns who had the temerity to question them. At the time that his work was first published in France, however, the Ramist controversy was at its height in England, especially at the University of Cambridge. The protagonists in this dispute, so far as published books were concerned, were Everard Digby and William Temple; but [190] the entire university was divided into two camps, with the uncompromising Aristotelians on one side and their Ramist opponents on the other. Digby, who became a fellow of St. John’s College and began to give public lectures in logic in 1573, was the leading spirit in the academic revival of Aristotelianism in England. But, at the very time he began his teaching, the influence of Ramus’ attack on the dialectics of Aristotle had already reached the stage where his books were being studied in place of the Organon. Remarks made by Gabriel Harvey in 1573 prove that Ramus’ philosophy was already well known at Cambridge, and sufficiently esteemed to be quoted by Harvey in support of his own criticisms of Aristotle’s ideas.[328] Harvey clearly belonged to the Ramist party in this controversy, and upheld the right to examine Aristotle’s ideas and reject those that did not agree with reason.[329]
William Temple, though not so familiar to posterity as Harvey, was the chief controversial writer for the Ramist party during this period.[330] He matriculated at King’s College in 1573, and later became a fellow of that college and taught logic in the university. He was secretary to Sir Philip Sidney from 1585 until the latter’s death, and afterwards was secretary to the famous Earl of Essex. Temple’s writings were mainly in support of Ramus’ system of logic against the Aristotelians, but the French philosopher’s writings on the mathematical sciences, of which we have spoken in the preceding chapter, also played an important role in this controversy. It was because Harvey was “a great and continual patron of paradoxis and a [191] main defender of straung opinions, and that communly against Aristotle too,”[331] that the fellows of Pembroke Hall attempted to oppose the granting of his M.A. in 1573. Harvey freely admitted the charge of defending against Aristotle such propositions as “Coelum non est quintae naturae,” but quoted Ramus and others as modern authorities whose validity equaled the Greek philosopher’s.
Nashe and Greene were of the opposing Aristotelian party, and it has been argued—quite rightly, I believe—that the animosity between the partisans of Ramus and of Aristotle at Cambridge during the eighties was one of the underlying causes of the ill-feeling of Greene and Nashe toward the Harveys.[332] Certainly, in the pamphlet warfare between Nashe and Harvey, one of the taunts which the former constantly hurls at the latter concerns Harvey’s presumption in criticizing Aristotle, and his support of Ramus. Dr. McKerrow wisely remarks that behind the conflict between Harvey and Nashe was “that ancient opposition between the old and the new, between servility and independence. . . . And it was the Harveys who stood for the future and Nashe for the past.”[333] In defending Harvey against the charges of his enemies, Dr. McKerrow says:
The charge of maintaining paradoxes and strange opinions is one of the most honourable which can be brought against a scholar or a scientist. It is a charge which has been brought against every man who has contributed to the progress of the world, and never yet was a nonentity so accused.[334]
Harvey’s eager curiosity in all matters pertaining to science, and particularly to astronomy, caused him to seek out the works and the company of the ablest scientists of his day. The list of men that Harvey cites in his writings and in his marginalia includes almost every important English scientific writer of the sixteenth century. He shows an acquaintance with the works [192] of most of these men, and must have had copies of their books in his own library, since many such volumes have survived that contain Harvey’s autograph and annotations.[335] He also knew several of the leading scientists personally. It is certain that he numbered Thomas Digges and John Blagrave among his acquaintances,[336] and through them he may have met some of the other scientific writers whose achievements he praised so warmly, and with whose works he showed such an intelligent familiarity.
Like the scientists we have discussed, Harvey had the vision of the practical utility of scientific research and the realization of the significant part skilled artisans as well as learned scholars must play in this essentially co-operative enterprise. In Pierces Supererogation he writes:
He that remembreth Humfrey Cole, a Mathematicall Mechaniciā, Matthew Baker a ship-wright, Iohn Shute an Architect, Robert Norman a Nauigatour, William Bourne a Gunner, Iohn Hester a Chimist, or any like cunning, and subtile Empirique, (Cole, Baker, Shute, Norman, Bourne, Hester, will be remembred, when greater Clarkes shalbe forgotten) is a prowd man, if he contemne expert artisans, or any sensible industrious Practitioner, howsoeuer Vnlectured in Schooles, or Vnlettered in Bookes. . . . and what profounde Mathematician, like Digges, Hariot, or Dee, esteemeth not the pregnant Mechanician? Let euery man in his degree enioy his due: and let the braue enginer, fine Daedalist, skilfull Neptunist, maruelous Vulcanist, and euery Mercuriall occupationer, that is, euery Master of his craft, and euery Doctour of his mystery, be respected according to the vttermost extent of his publique seruice, or priuate industry.[337]
The diversity of Harvey’s scholarly interests, and the learned, if not pedantic, cast of his mind made him a particularly ardent supporter of the Renaissance conception of poetry as a learning. No one believed more strongly than he that the function of a great poem was to epitomize all important knowledge in both natural and moral philosophy. Harvey expressed this ideal in the notes he wrote on the flyleaf at the beginning of one of his volumes, wherein five small books, one of which had been given to him by his friend Edmund Spenser, were bound together.
Other commend Chawcer, & Lidgate for their witt, pleasant veine, varietie of poetical discourse, & all humanitie: I specially note their Astronomie, philosophie, & other parts of profound or cunning art. Wherein few of their time were more exactly learned. It is not sufficient for poets, to be superficial humanists: but they must be exquisite artists, & curious vniuersal schollers.[338]
As a “curious vniuersal scholler,” Harvey fully lived up to the Renaissance ideal he expressed so succinctly; but he unfortunately was not endowed with any poetic genius. Though he himself lacked the art to make truly poetic use of recondite scientific knowledge, he took particular delight in poetry based upon sound learning. He especially admired the astronomical descriptions in Chaucer and Lydgate, and considered them “much better learned then owre moderne poets.”[339] He pointedly complained of Spenser’s comparative ignorance of astronomy, because he considered a mastery of that science essential to a great poet:
Pudet ipsum Spenserum, etsi Sphaerae, astrolabijque non planè ignarum; suae in astronomicis Canonibus, tabulis, instrumentisque imperitiae. Praesertim, ex quo vidit Blagraui nostri Margaritam Mathematicam. Qui né Pontano quidem, aut Palingenio, aut Buchanano, aut etiam Bartasio cedit, exquisita vtriusque Globi, astrolabij, baculique familiaris scientia. Vt alter iam Diggesius, vel Hariotus, vel etiam Deius videatur. Aureum calcar non rudium aemulorum.[340]
A rereading of the astronomical passages in Spenser’s poems enforces the truth of Harvey’s criticism. Spenser’s knowledge of astronomy may seem very extensive to the modern reader, for the average educated person of today is often completely ignorant of even the elementary principles of the stellar motions, whereas his Elizabethan counterpart would at least have known as much as was contained in some simple textbook like Sacrobosco and would have been able to recognize the most important constellations in the heavens.
Beyond this minimum level of astronomical lore that was the common possession of all his educated contemporaries Spenser, apparently, never rose. He never acquired Chaucer’s easy familiarity with the actual processes of astronomical observation and computation, which enabled the author of the Canterbury Tales to fix the season or the time of day by poetic, yet exact, references drawn from the science of astronomy.[341] It was this poetic use of material derived from the precise learning of the scholar and scientist that Harvey so greatly admired in Chaucer and earnestly wished to have Spenser imitate. An instance of the sort of careless handling of astronomical data that annoyed Harvey is found in the passage in Book I, Canto iii, of the Faerie Queene, where Una and her lion seek refuge for the night in the cottage of Abessa and Corceca. The poet indicates the passage of time during the night, and the arrival of an hour about midnight or somewhat later, by the lines:
Now when Aldeboran was mounted hie
Aboue the shynie Cassiopeias chaire,
And all in deadly sleepe did drowned lie,
One knocked at the dore, and in would fare; . . .[342]
It so happens that this situation of Aldebaran with respect to Cassiopeia during the midnight hours can only occur during the winter months, whereas the entire setting of the poem is in summertime.[343]
Here, however, is not the place to discuss Spenser’s cosmological ideas, nor his use of astronomical material in his poetry. Certain it is that he did not, like his friend Gabriel Harvey, keep in close touch with the latest scientific investigations and theories in his own day. His poetry, although reflecting many of the currents of thought that inspired the new scientific movement, seems never to have been directly influenced by any of the events in its progress.[344]
Gabriel Harvey was only one among many English scholars whose interest in the mathematical sciences was doubtless strengthened as a result of the Ramus-inspired controversy between the old and the new learning, which raged at Cambridge while he was a member of the university. A number of other men who later contributed to the spread of mathematical and scientific knowledge were students at Cambridge during this period. The principal ones, including William Kempe, William Bedwell, and Thomas Hood, testified to the influence of Ramus and his books in arousing an interest in science by their references to him in their writings, and by their translations of Ramus’ mathematical works into English.[345]
Had it not been for the Ramist influence, mathematics and science would probably have been seriously neglected at Cambridge during the last three decades of the sixteenth century. The Edwardian Statutes of 1549, in whose formulation Sir John Cheke and Sir Thomas Smith had had an important share, had given increased importance to the mathematical sciences in the university curriculum.[346] The Statutes of Elizabeth of 1572, however, had completely omitted mathematics from the prescribed undergraduate course.[347] The attitude which regarded the mathematical sciences as practical subjects not proper for university study was probably characteristic of the Aristotelian party in the universities, and had much to do with the transfer of scientific scholarship and research to London.[348] This shift, as we have already remarked, was unquestionably of great advantage to the progress of science, not only because of the greater interest in its utilitarian value that prevailed in the metropolis, but also because it brought the scientific scholars into closer contact with the artisans concerned with the development of the various technical arts.
It would be entirely wrong, however, to conclude that there was a universal antipathy to science in university circles. At Oxford, during the seventies, Henry Savile had lectured on the Almagest and Richard Hakluyt the younger on geographical science.[349] At Cambridge those who sided with the Ramist party were naturally disposed to give an important place to the mathematical sciences and to show an interest in their development and practical application. It was at Cambridge, and during this very period, that the most influential popular teacher of those sciences in the last twelve years of the sixteenth century received his training. This teacher was Thomas Hood, who proceeded from the Merchant Taylors’ School in London to Trinity College, Cambridge, in 1573, graduated B.A. in 1577-78, and commenced M.A. in 1581. For a time he was a fellow of Trinity, but later returned to his native London. There he [197] became the first man to hold a publicly endowed lectureship in the mathematical sciences in that city, and it is as the first Mathematical Lecturer that he merits a most important place in the history of English science.
We have already noted how, during the reign of Elizabeth, scientific scholarship and investigation, as represented by Digges, Dee, and their pupils and fellow workers, had shifted from the universities to London. A scientific academy supported by the state was a project greatly desired by several farsighted men of the time who realized the valuable services it might render to the commonwealth. John Dee had this idea in mind when, in his “Compendious Rehearsall,”[350] he petitioned Elizabeth for the “Mastership of Saint Crosses,” because its location and its buildings were more suitable than any other place for the scientific academy he wished to establish. Earlier than this, in 1572, Sir Humphrey Gilbert had drawn up a memorandum for the “erection of an Achademy in London for educacion of her Maiestes Wardes, and others the youth of nobility and gentlemen,”[351] which he addressed to Queen Elizabeth. The mathematical sciences were given a very important place in his plans, which called for two professors of mathematics, in addition to one engineer and three ushers or assistants. The application of these sciences to military fortifications and gunnery and to geography and navigation was to be particularly stressed. Gilbert, furthermore, made a special point of insisting upon his professors’ making contributions to scholarship by means of regular publications. He required each of his public readers or professors to set forth in print at least one new book every six years, and those who taught languages had to translate into English and publish at least one important foreign book every three years.[352]
Nothing came of Gilbert’s proposal; nor did Richard Hakluyt’s persistent efforts, from 1582 onwards, to procure the [198] endowment of a public Lecture on Navigation for the better training of English mariners meet with success.[353] Like most farsighted programs, they were allowed to languish until a crisis finally stirred the government and the leading citizens to action. In 1588 the threat of invasion by Spain, even after the Great Armada had been dispersed, kept the capital in constant dread of a sudden attack. The City of London, with the consent and supervision of the Privy Council, proceeded to organize a militia for its defense in case of emergency. Captains and other officers were chosen, and rules laid down for the discipline and training of the troops. In order to provide for the better instruction of the captains of these trained bands, several of the leading citizens contributed to the establishment of a Mathematical Lecture under the direction of the Lord Mayor and the Aldermen of the City of London.[354] Thus was [199] the first public lecture in the mathematical sciences created in London in the year 1588.
Thomas Smith, the wealthy merchant who in 1600 was to become the first governor of the East India Company, was the leading spirit in the founding of this lecture. Through his influence, apparently, Thomas Hood, a Londoner and son of a member of the Merchant Taylors’ Company, was chosen as reader.[355] The first lecture was delivered before an audience assembled at the house of Thomas Smith on the fourth of November, 1588. The charming and most appropriate speech which Hood made on this occasion has been preserved, for, either through Smith’s influence or because of the general public interest in the event, it was printed by Edward Allde, with the title: A Copie of the Speache: Made by the Mathematicall Lecturer, unto the Worshipfull Companye present. At the house of the Worshipfull M. Thomas Smith, dwelling in Gracious Street: the 4. of Nouember, 1588. T. Hood.
Hood’s audience was not to be limited to the captains of the trained bands of London. The lectures, after the first, were usually delivered in the Staplers’ Chapel in Leadenhall—in the very center of commercial London—and were open freely to the public.[356] From the auspices under which they were instituted, one would naturally infer that Hood’s lectures would be designed to stress the practical applications of science. In fact, Hood himself makes this purpose clear in his opening speech, [200] and in the prefaces to his various books. He was nevertheless insistent that his pupils begin by mastering the fundamental principles of the mathematical sciences, and set out first of all to instruct his auditors in the elements of arithmetic, geometry, and astronomy. After his students were thoroughly grounded in these subjects, he passed on to their application in the construction and use of instruments and maps, and in the solution of practical problems in surveying and navigation. Hood kept the needs of his pupils constantly in mind, and adapted his teaching to the demands imposed by an audience made up almost wholly of eager artisans, soldiers, and seamen, who had had little scholarly training but were inflamed with a passionate desire for useful knowledge.
Thomas Hood was by no means as learned a scholar in mathematics and astronomy as Recorde had been, but he was an excellent teacher and employed many of Recorde’s methods and devices. He imitated Recorde in his emphasis upon the proper order in teaching, refusing to take up more advanced topics until the elementary principles of a subject had been thoroughly mastered.[357] Like Recorde, he composed many of his works in the form of dialogues, and he could write English prose in a style that was remarkable for its simplicity and conciseness, and its mastery of the art of clear exposition. He lacked Recorde’s humor, however, and his ability to infuse a truly dramatic quality into his dialogues on scientific subjects.
The intelligence with which Hood adapted his teaching to the capacities of his more humble auditors deserves the highest praise. He realized that the splendid textbooks published by Recorde, desirable as they might have been for use by his classes, were far too costly for the purses of most of his pupils.[358] Instead, [201] he needed simple, inexpensive textbooks which merely printed the statements of the fundamental propositions to be explained and demonstrated in the lectures—something, in short, which would correspond to the modern syllabus, and could be sold for a penny or two at the most. For the use of the celestial globe he found such a handbook already in print: Charles Turnbull’s A perfect and easie Treatise of the vse of the coelestiall Globe[359] served for some time as the textbook which Hood amplified in his lectures on the elements of astronomy.[360]
For the benefit of his classes in geometry, Hood translated the statements of the definitions, axioms, and propositions in Ramus’ Geometriae, leaving out all diagrams and demonstrations, and had them issued in a little pamphlet to be sold as a syllabus at his lectures.[361] His pupil, Francis Cook, made a similar epitome of a work by Georg Henisch, which he published in 1591 as The Principles of Geometrie, Astronomie, and Geographie.[362]
Several of Hood’s own works were printed during his tenure as Mathematical Lecturer.[363] They were based upon his earlier lectures, and were designed, in part, to be used as textbooks for future classes.[364] From them we may gain a clear idea of both the manner and the subject matter of Hood’s teaching. Of particular interest is his treatise, The Vse of both the Globes, which was written at the special request of William Sanderson, one of the great patrons of the English voyages and maritime adventures, in order to explain the two globes recently designed by Emery Molyneux and constructed at Sanderson’s expense. Hood’s book, issued in 1592, was the earliest treatise on the Molyneux globes, for not until 1594 was the Latin work on these globes, composed in 1593 for Sanderson by Robert Hues, first printed.[365] The Vse of both the Globes describes, [203] in dialogue form, a scientific lecture, in which the Master (the author) is imagined with the Molyneux globes in front of him, and his words, as he proceeds with a direct, physical demonstration of the use of the globes to his attentive pupil, are faithfully recorded, along with the intelligent questions asked by the student.
Because of the essentially practical character of these mathematical lectures, Hood’s consideration of astronomy was naturally directed chiefly to its application to the problems of navigation. He was therefore mainly concerned with explaining the use of astronomical instruments, such as the astrolabe, the celestial globe, the cross-staff, and the sector or quadrant. Consequently, the geocentric system was necessarily the basis of the descriptions in his works. There was no occasion to go into theoretical astronomy and therefore we cannot be certain of Hood’s own attitude toward the Copernican hypothesis. He constantly referred to Copernicus’ figures and calculations, however, and adopted many of them in his two treatises on the globes, just as Thomas Hill had done.
Next to Recorde’s Castle of Knowledge, Hood’s books on the globes give the best and clearest exposition of that branch of astronomical science to be found in any sixteenth-century English book. Although, because they were definitely utilitarian in aim and restricted in subject matter, their author had no reason to turn aside from the geocentric astronomy of actual observation to deal with controversial theories, it is interesting to note that in The Vse of the Celestial Globe in Plano he digresses to give a lengthy account of the nova of 1572—the longest contemporary account to be published in English. Hood’s discussion of the various suppositions concerning the nature of the new star in Cassiopeia is of special significance in connection with the dissemination of the new astronomical ideas in England:
. . . That starre appeared of so great a bignesse and light at the first, that it seemed to exceede the Euening starre: but within certaine moneths it did so diminish, that it was iudged to be but equall to the Pole starre: in that quantitie it continued vnto the ende. It was a thing most strange [204] and wonderfull, whereby the wittes of many men were set on worke. Some men thought it to be in the firmament, wherein the rest of the fixed starres are, but they saide it was not any newe starre, but onely one of those thirteen which by consent of all Astronomers are ascribed to Cassiopeia. The cause why it seemed greater, saide they, was a certaine exhalation comming at that time betweene our sight and it, in the vpper Region of the Aire: and thereby it came to passe, that many men thought it to be a newe starre.
Others affirmed this starre to bee some one of those, which because of their smalnesse cannot well bee scene, yet by reason of an exhalation comming betweene our sight and it, it seemed at that time to be so great, that it was accounted of all men to be a new starre. To conclude, others denied it to be in the firmament, and therefore iudged it not to be a starre, but a comet ingendred in the vpper region of the aire. None of these opinions seemed true to the best Astronomers. For first, they found it out for certaintie, that there were 13. starres in Cassiopeia besides this. Secondly, if the exhalation whereof they talke was so great as they sayd it was, that it made the star to blaze both in England, France, Germanie, Italie, and Spaine, howe came it to passe, that it should make that starre alone to blaze, and none other in the constellation of Cassiopeia? Thirdly, it appeareth by this, that it was no comet, in that the chiefest Astronomers alwayes noted this starre to haue one and the same situation with the rest of the starres next adioyning vnto it, without any diuersitie either in time, or place. For as it was placed at the first with the other starres, so was it placed afterwards continually, and so it appeared to vs here in England, and to them in France, Germanie, or els where. Which thing being so, wee may well affirme that it was not in the vppermost region of the ayre, where other comets are ingendred, but that it was at the least aboue the moone. For no comet at any time hath beene scene in diuers regions vnder one and the same part of heauen; where as this starre appeared alwayes in and vnder one place; so that it could not bee a comet. The best Astronomers therefore concluded thus, that that new starre, whatsoeuer it was, had his place in the firmament, being thereto induced by this argument: because none of them could obserue in it any other motion then that, which vsually they obserue in all the fixed starres. For it kept a most certaine and constant motion and the selfe same situation, and distaunce from other fixed starres. If it had beene in any of the spheres of the Planets, it must needs haue moued some other way, and not haue kept one and the same place, considering that the Planets do alwayes shift from place to place, and are neuer in equall distance from any of the fixed starres. This argument also doth conclude, that much lesse this starre could be in the elementall region, because it is vnpossible that there any thing should keepe either a certaine place, or a certaine motion. And therefore it seemed, that that starre was either newly created by [205] Almightie God in the firmament, or els certainly it is possible for a comet to be ingendred there.[366]
Certainly, the auditors of Hood’s mathematical lectures could not well retain their faith in the Aristotelian astronomy, with its doctrine of the immutability of the heavens.
The original grant for the Mathematical Lecture covered only two years. Sometime during the winter of 1589-90, however, the Privy Council, in a document sent to the Lord Mayor concerning the permanent organization and discipline of the trained bands of the City of London, ordered the continuance of the lectures for at least two more years.[367] The influence of both Walsingham and Burghley was exerted to persuade the original contributors to the funds for the Mathematical Lecture to renew their support, and to obtain from the Lord Mayor and the Aldermen a guarantee of Hood’s stipend for the additional two-year period. The lectures in the Staplers’ Chapel in Leadenhall continued to be delivered regularly until 1592. How much longer the institution of the Mathematical Lecture survived is uncertain; but it had definitely been abandoned before 1596.[368] Nevertheless, London was not long to be without regular public lectures in the mathematical sciences, for in 1597 the professors of astronomy and geometry in the newly established foundation of Gresham College began their teaching.
The last decade of the sixteenth century, so significant in the history of English literature because both in poetry and the drama England could at last claim productions of major [206] rank, was marked by a noteworthy resurgence of cosmological writings. Recorde’s Castle of Knowledge saw a new edition in this decade.[369] Digges’s Prognostication euerlasting was at least twice reprinted, and the works by Hood and Hill issued during these years have already been discussed. Two other important works published during the nineties contributed greatly to the popularizing of astronomical learning and the spread of the Copernican astronomy. These were Thomas Blundeville’s Exercises and John Blagrave’s Astrolabium Vranicum Generale.
Thomas Blundeville, like Thomas Hill, was an omniscient compiler of popular books on every type of knowledge. The first edition of his Exercises (1594)[370] was a thick quarto volume, containing treatises on arithmetic, cosmography, the use of the globes, the universal map of Peter Plancius, John Blagrave’s Mathematical Jewel, and the principles of navigation. Two more treatises, on maps and Ptolemy’s tables, which had been published separately in 1589, were added to the second edition in 1597 and included in all subsequent editions, the second issue of the seventh edition being published as late as 1638.
Blundeville’s works were justly admired by his contemporaries because of the clarity of his English style and the simplicity of his expositions of complex scientific matters. His books were deservedly popular, and represent the highest type of conscientious compilations by an author who was not an original scientist himself but was eager to expound, in simpler language for the intelligent layman, the more important scientific ideas and discoveries of his time. He was on friendly terms with the best scientists of his day in England, such as Digges, Dee, Norman, Hood, William Gilbert, and Edward Wright, and sought to incorporate the results of their [207] latest investigations in his popular books.[371] Blundeville was at his best when condensing and simplifying an abler man’s work in order to make it easier for the average student to comprehend its essential features. This was what he did with Blagrave’s Mathematical Iewel,[372] in which the latter described the improved type of astrolabe which he had invented, and explained the method of using it.
In his treatise on cosmography, however, Blundeville took the conservative course, and made his compilation from the traditional authorities, whose data were derived, ultimately, from the work of Alfraganus and the compilers of the Alfonsine Tables. His was the last important English scientific textbook dealing with astronomy which described the old system without any essential modifications.[373] Even so, he gave Copernicus’ figures in many places, as Hill and Hood had done, and showed familiarity with the calculations based upon the De revolutionibus. In his rejection of the Copernican theory he exhibited a clear realization of its mathematical advantages, while offering the usual Aristotelian and theological objections:
Some also deny that the earth is in the middest of the world, and some affirme that it is mooueable, as also Copernicus by way of supposition, and not for that he thought so in deede: who affirmeth that the earth turneth about, and that the sunne standeth still in the midst of the heauens, by helpe of which false supposition he hath made truer demonstrations of the motions & reuolutions of the celestiall Spheares, then euer were made before, as plainely appeareth in his booke de Reuolutionibus [208] dedicated to Paulus Tertius the Pope, in the yeare of our Lord 1536. But Ptolomie, Aristotle, and all other olde writers affirme the earth to be in the middest, and to remaine unmooueable and to be in the very Center of the world, proouing the same with many most strong reasons not needefull here to be rehearsed, because I thinke fewe or none do doubt thereof, and specially the holy Scripture affirming the foundations of the earth to be layd so sure, that it neuer should mooue at any time: Againe you shall finde in the selfe same Psalme these words, Hee appointed the Moone for certaine seasons, and the Sunne knoweth his going downe, whereby it appeareath that the Sunne mooueth and not the earth.[374]
Blundeville was wrong, however, in his estimate of the number of adherents to the Copernican theory among his countrymen. In 1596 John Blagrave, whom he had so highly praised and whose “Mathematical Jewel” he had recommended and described, designed his “Uranical Astrolabe” in accord with the new Copernican theory, and proclaimed in no uncertain terms his adherence to the heliocentric system. The very title-page of Blagrave’s book asserts this idea, for it reads:
Astrolabium Vranicum Generale, A . . . solace . . . for Nauigators . . . Containing the vse of an Instrument or generall Astrolabe: Newly for them deuised by the Author, to bring them skilfully acquainted with all the Planets, Starres, and constellacions of the Heauens: and their courses, mouings, and apparences, called the (Vranicall Astrolabe.) In which, Agreeable to the Hipothesis of Nicolaus Copernicus, the Starry Firmament is appointed perpetually fixed, and the earth and his Horizons continually mouing from West towards the East once about euery 24 houres. . . . Compyled by Iohn Blagrave of Reading Gentleman, the same wellwiller to the Mathematicks. Anno. 1596. Printed by Thomas Purfoot, for William Matts.
Blagrave’s detailed description of the construction and use of this astrolabe does not concern us here. What is significant, however, is that his, apparently, was the first attempt to modify the older types of astrolabes in order to make them illustrate the principle of relative motion that was at the basis of the Copernican theory. In all earlier astrolabes, the more important fixed stars had been represented on a movable plate of pierced [209] metal, resembling a net or spider’s web, and called the “rete.” This plate rotated in the shallow, circular space of the fixed plate, called the “mother,” on which the azimuth and altitude lines were engraved. In Blagrave’s astrolabe, however, a star map of the heavens was engraved on the fixed plate, and the earth, or rather the moving horizon of the terrestrial observer, was represented by a moving rule and scale, the “zenitfer.”[375]
Blagrave constantly emphasizes the way in which his instrument is designed according to the theory of Copernicus and illustrates the principles upon which the latter’s system was based. He says: “Needlesse it is to stand vpon the Fabrication, or long particularizing of this Instrument or his partes, since they are but the Copernician representation of the constellations fixed, and the 90 generall Horizons moouing.”[376] Later he expounds this idea at greater length:
I do not stand making speciall Chapters of the vse of the particular moouer in the 1 Cap. mentioned, because it consisteth but of the very same Horizon circle and 12 houses of one perticular latitude, which old I. Stophlerus, and our old english Laureat G. Chaucer, haue so largely and plainely written of: withall, being a thing most commonly in vse, and differing in nothing, but that they according to the auncient Astronomers, appointed the Starry Heauens to mooue rightwards from East towards West, vppon the earth or fixed Horizon of the place. And I according to Copernicus cause the earth or Horizon to moue leftwards from West towards East, vppon the Starry Firmament fixed: In so much, that if in this my Astrolabe you hold still that perticular moouer with one hand, and with your vnder hand turne about the Celestiall, then is it iumpe Stophler againe. In which motion (a pretty thing to note) one that standeth by shall hardly perceiue any other but that the Reete mooueth, although in deede you turne about the Mater, strongly confirming Copernicus Argument, who sayth, that the weakenesse of our senses do imagine the Heauens to mooue about euery 24 houres from East to West by a Primum mobile, where as in deede they [210] haue been alwayes fixed, and it is the earth that whirleth about euery 24 houres from West to East, of his owne propper nature allotted vnto him, as most fit for the receptacle of all transitory things, being appointed in a place where nothing is to stay him from his continuall moouing.[377]
As Blagrave pointed out so explicitly in this passage, the difference between his uranical astrolabe and the other types furnished an excellent mechanical demonstration of the two possible interpretations of the apparent motion of the heavens. The skilled artisans or “mechanicians,” who were playing an increasingly important part in the development of English science, would readily appreciate this fact, and Blagrave’s outstanding reputation as a designer of instruments of this sort would win him a respectful hearing among all classes interested in astronomy. Except for his friend Thomas Digges, Blagrave probably did more than any other sixteenth-century Englishman to disseminate an intelligent knowledge of the Copernican theory.
With the publication of Blagrave’s Astrolabium Vranicum Generale, sound information about the mechanical details of the new heliocentric astronomy became readily available to all his countrymen. English readers of scientific books in the late sixteenth century had found the Copernican hypothesis mentioned with respect by even the most conservative among the contemporary writers of recognized standing. Not one of the leading scientists had vigorously opposed the new system, as had happened on the Continent, where such eminent astronomers as Christopher Clavius and Tycho Brahe were determined adversaries of the heliocentric theory. On the contrary, the English scientists of the highest popular renown, such as Recorde, Dee, Digges, and Blagrave, had championed the new system—the two latter in the strongest possible terms. The ground had thus been well prepared in England for the next logical step in the advance of the Copernican astronomy: the search for new physical facts which would tend to establish more firmly the scientific validity of the Copernican hypothesis.
The remarkable growth of popular interest concerning the science of astronomy is one of the most significant features of the last decade of the sixteenth century. The group of enthusiastic students of astronomy centering about Sir Walter Ralegh and his friend and mathematical adviser, Thomas Harriot—so much discussed recently in connection with Shakespeare’s topical references to the “School of Night”[378]—was only the most noted example of a movement that was widespread, and whose influence was felt in many fields not directly related to scientific investigation. The force of this movement was still at its height in the early years of the seventeenth century. In one of its aspects, the growing interest in astronomy was essentially practical and directly concerned with its application to navigation. On the other hand, the less immediately useful study of the theoretical phases of astronomy was receiving the attention of many of the ablest minds.
Because of the greater popular interest in the mathematical theories of the planetary motions, there was now a demand for an advanced work on this subject in English. No English textbook of astronomy printed before 1600 had attempted any detailed consideration of that more advanced phase of the science known as the “theoricks of the planets”—that is, the method of computing the motions of the planets in their orbits. Recorde, in his Castle of Knowledge, had promised to take up the subject in a later treatise.[379] Most of the earlier English astronomical writers had considered the “theoricks” too complex for a popular work in the vernacular.
In 1602, however, Blundeville published his Theoriques of the seuen Planets,[380] in response to the rapidly increasing desire for a book on theoretical astronomy. Without the assurance of a large sale, so expensive a publication as this thick quarto with its many diagrams would not have been undertaken by any printer. Blundeville, in his preface, mentions the great interest in geography and astronomy existing among the “Gentlemen of the Innes of Court” and suggests that they had been the chief purchasers of his Exercises.[381]
Blundeville’s Theoriques, like his earlier works, was a compilation and synthesis based upon the books of several different writers on the subject. He tells us it had been “collected, partly out of Ptolomey, and partly out of Purbachius, and of his Commentator Reinholdus, also out of Copernicus, but most out of Mestelyn, whom I haue cheefely followed, because his method and order of writing greatly contenteth my humor.”[382] Fundamentally, the work is the Theoricae novae planetarum of Peurbach, brought up to date by comparison with the books of the ablest subsequent writers and commentators. The planetary motions are portrayed according to the ancient theories, with the various epicycles inclosed within solid eccentric orbs.
When Blundeville compiled this last treatise of his, he was already an old man and he probably did not live to see the march of astronomical progress make his work obsolete within a decade.[383] In fact, of the advanced books on astronomy printed in England, Blundeville’s was the last which presented the old system without any radical modifications. It is true that many of the cheap popular handbooks of knowledge, hastily compiled or translated by hack writers, continued for many decades to portray the old Ptolemaic system of the celestial spheres, and to expound the Aristotelian physical doctrines upon which it was based. Robert Allot’s Wits Theater of the Little World[384] [213] and Scipio Du Plessis’ The Resoluer; or Curiosities of Nature[385] are typical examples. In these books concise information upon every imaginable topic was to be found; such divergent subjects as “Angels,” “Dicing,” and “Chastity” were included among the classified headings into which they were divided. These cheap compendia of universal lore would not pass for authoritative works among the judicious and intelligent, any more than similar works today would be accorded scientific standing.
In the late sixteenth century, as we have already observed, all English books of recognized scientific merit which dealt with the construction of the universe had either espoused the new Copernican theory, or, if they expounded the old system, had at least included a respectful notice of the new hypothesis. In the seventeenth century we shall find that all such works written subsequent to Blundeville’s Theoriques abandoned the old astronomy, and portrayed either the heliocentric system or a new and radically different geocentric system, designed so as to incorporate the recent astronomical discoveries.[386] The advance of knowledge had made the Aristotelio-Ptolemaic cosmology, in its traditional form, wholly untenable, and this was clearly realized by the English scientific writers.
The old Aristotelian system of the universe, as has been noted in an earlier chapter,[387] had provided Ptolemy’s mathematical [214] astronomy with a complete physical basis, consisting of the tangible machinery of material spheres to move the planets in their orbits. In addition, the doctrine of the four sublunary elements, plus the fifth element, or ether, gave the sanction of classical Greek mechanics to a geocentric universe. The elements earth and water, in which the principle of gravity predominated over the principle of levity, naturally sought the center of the universe, and the resulting globe, our earth, must of necessity surround the central point of the entire material world.
The physical foundations of this Aristotelian system had been disastrously shattered, however, by the research in connection with the new star of 1572, the comet of 1577, and the other comets that appeared in the last two decades of the sixteenth century. The astronomical observations contradicted the theory of solid orbs, disproved the doctrine of the immutability of the heavens above the moon, and made it seem probable that the matter of the heavens was not essentially different from sublunary matter.
With the overthrow of the celestial mechanics of Aristotle the conservatives lost one of their principal arguments. More than ever, then, from the scientific point of view, the conflict became one between two purely mathematical systems, one simpler than the other, but both able to represent the observed motions of the stars and planets. In the physical realm, the arguments for each side were based upon the balancing of probabilities. Fair-minded scholars debated whether, for example, the motions assigned by Copernicus to the earth were more credible, mechanically, than the tremendous speeds at which the outer spheres must rotate if the Ptolemaic system were true. All scientists realized that if they could discover some new physical principle which would account for the motions that Copernicus gave to the earth, the case for the latter’s hypothesis would be materially strengthened. In short, the old system had had a physical basis which recent discoveries had proved false; the new system had yet to find satisfactory physical [215] explanations for the assumptions upon which its mathematical demonstrations had been erected.[388]
The Copernican system was not to have a complete mechanical demonstration until Newton published his Principia in 1687. But English scientists, for more than a century before this, had been seeking new observations and discoveries which would contribute toward ascertaining the true construction of our universe. Thomas Digges, in 1573, had made an ardent plea for a comprehensive program of astronomical research with that end in view. The immediate line of investigation which Digges had suggested—the careful determination of the annual parallax of the nova of 1572 and of other stars in order to demonstrate geometrically the earth’s revolution about the sun—was to prove fruitless until the nineteenth century. This failure to detect an annual parallax in any of the stars was used as a strong argument against the heliocentric system by Tycho Brahe and other opponents of the Copernican theory.
A new approach was opened up by Digges’s countryman, William Gilbert (1540-1603).[389] If we bear in mind the state [216] of astronomical thought among English scientists at the end of the sixteenth century, we can readily understand the working of Gilbert’s mind when he discovered not only that the earth had magnetic properties, but also that his magnetized sphere, or terrella, rotated under the influence of a magnetic field. It was inevitable that he should seize upon these facts as a physical explanation of Copernicus’ hypothesis of the rotation of the earth. The earth’s magnetism would also provide a reason why heavy objects sought its center, making recourse to Aristotle’s principles of gravity and levity entirely superfluous, and would account for the failure of the centrifugal force of the rotating earth to cause objects to fly violently from its surface.
The whole of the sixth book of Gilbert’s great work, the De Magnete, is given over to the exploitation of his magnetic discoveries as a proof of the truth of one phase of the Copernican theory. Gilbert never committed himself so positively on the question of the earth’s revolution about the sun. He was no doubt deterred from this step by the fact that he had no scientific evidence to offer concerning this feature of the Copernican system. His attack upon the idea of the rotation of the heavens, on the other hand, was filled with scorn for the Aristotelians who upheld that hypothesis. To enforce his point, he adopted without qualification Digges’s idea that the stars were infinite in number, and located at varying and infinite distances from the center of the universe.[390] In the third chapter of his sixth book, entitled “On the magnetick diurnal revolution of the Earth’s globe, as a probable assertion against the time-honoured opinion of a Primum Mobile,” Gilbert says:
But, in the first place, it is not likely that the highest heaven and all those visible splendours of the fixed stars are impelled along that most rapid and useless course. Besides, who is the Master who has ever made [217] out that the stars which we call fixed are in one and the same sphaere, or has established by reasoning that there are any real and, as it were, adamantine sphaeres? No one has ever proved this as a fact; nor is there a doubt but that just as the planets are at unequal distances from the earth, so are those vast and multitudinous lights separated from the earth by varying and very remote altitudes; they are not set in any sphaerick frame or firmament (as is feigned), nor in any vaulted body: accordingly the intervals of some are from their unfathomable distance matter of opinion rather than of verification; others do much exceed them and are very far remote, and these, being located in the heaven at varying distances, either in the thinnest aether or in that most subtle quintessence, or in the void; how are they to remain in their position during such a mighty swirl of the vast orbe of such uncertain substance. . . .
How immeasurable then must be the space which stretches to those remotest of fixed stars! How vast and immense the depth of that imaginary sphere! How far removed from the Earth must the most widely separated stars be and at a distance transcending all sight, all skill and thought! How monstrous then such a motion would be![391]
Although Gilbert’s explanation of the rotation of the earth in terms of magnetism was not conclusively demonstrated, since he failed to evolve any laws of dynamics which would establish the connection between the motions of the earth and the planets and the action of magnetic forces, it was highly regarded by his contemporaries. It was praised by Kepler and Galileo and other leading scientists, who accepted it as a tentative hypothesis. Not only did it hold an important place in astronomical theory until the time of Newton, but it also stands out with special prominence in the historical background of Newton’s own work in evolving the theory of gravitation.
Outstanding among the English mathematicians who announced their acceptance of the idea of the earth’s rotation, as a result of Gilbert’s work, was Edward Wright (1558-1615). Popular acclamation among his contemporaries ranked Wright along with Recorde, Dee, Digges, and Harriot, as the five [218] greatest mathematicians in Elizabethan England. His services to the theory of navigation, through his computation of the loxodromic curves in order to correct the projection used in making maps, is universally recognized.[392] Wright was a friend of William Gilbert, and wrote a long preface to the De Magnete, in which he proclaimed in the following terms his belief in the rotation of the earth:
Finally, as to the views which you discuss in regard to the circular motion of the earth and of the terrestrial poles, although to some perhaps they will seem most supposititious, yet I do not see why they should not gain some favour, even among the very men who do not recognize a sphaerical motion of the earth; since not even they can easily clear themselves from many difficulties, which necessarily follow from the daily motion of the whole sky. For in the first place it is against reason that that should be effected by many causes, which can be effected by fewer; and it is against reason that the whole sky and all the sphaeres (if there be any) of the stars, both of the planets and the fixed stars, should be turned round for the sake of a daily motion, which can be explained by the mere daily rotation of the earth. Then whether will it seem more probable, that the aequator of the terrestrial globe in a single second (that is, in about the time in which any one walking quickly will be able to advance only a single pace) can accomplish a quarter of a British mile (of which sixty equal one degree of a great circle on the earth), or that the aequator of the primum mobile in the same time should traverse five thousand miles with celerity ineffable; and in the twinkling of an eye should fly through about five [219] hundred British miles, swifter than the wings of lightning, (if indeed they maintain the truth who especially assail the motion of the earth). Finally, will it be more likely to allow some motion to this very tiny terrestrial globe; or to build up with mad endeavour above the eighth of the fixed sphaeres those three huge sphaeres, the ninth (I mean), the tenth, and the eleventh, marked by not a single star, especially since it is plain from these books on the magnet, from a comparison of the earth and the terrella, that a circular motion is not so alien to the nature of the earth as is commonly supposed. Nor do those things which are adduced from the sacred Scriptures seem to be specially adverse to the doctrine of the mobility of the earth; nor does it seem to have been the intention of Moses or of the Prophets to promulgate any mathematical or physical niceties, but to adapt themselves to the common people and their manner of speech, just as nurses are accustomed to adapt themselves to infants, and not to go into every unnecessary detail. Thus in Gen. i. v. 16, and Psal. 136, the moon is called a great light, because it appears so to us, though it is agreed nevertheless by those skilled in astronomy that many of the stars, both of the fixed and wandering stars, are much greater. Therefore neither do I think that any solid conclusion can be drawn against the earth’s mobility from Psal. 104, v. 5; although God is said to have laid the foundations of the earth that it should not be removed for ever; for the earth will be able to remain evermore in its own and self-same place, so as not to be moved by an wandering motion, nor carried away from its seat (wherein it was first placed by the Divine artificer). We, therefore, with devout mind acknowledging and adoring the inscrutable wisdom of the triune Divinity (having more diligently investigated and observed his admirable work in the magnetical motions), induced by philosophical experiments and reasonings not a few, do deem it to be probable enough that the earth, though resting on its centre as on an immovable base and foundation, nevertheless is borne around circularly.[393]
Wright’s words and attitude are those of the cautious scientist, unwilling to go further than the available experimental data warrant, and accurately express the scientific import of Gilbert’s discoveries as they affected the acceptance of the Copernican theory. After 1600 almost every English scientist followed Gilbert and Wright in adopting the idea of the rotation of the earth. By no means all of them, however, were ready to go so far as to pronounce definitely in favor of the belief in the earth’s revolution about the sun, because the [220] scientific evidence for that hypothesis was less convincing and the objections to it had not yet been weakened by new discoveries. Consequently, the more conservative among the scientific writers supported a geocentric system which combined the rotating magnetic earth of Gilbert with the arrangement of the planets proposed by Tycho Brahe. It was Tycho’s system, or the modification of it made by the followers of William Gilbert, that was opposed to the Copernican system in all the important English astronomical treatises after 1602. A knowledge of Tycho’s work and of the scientific basis and validity of his system is therefore essential to an understanding of the astronomical literature of the seventeenth century.
Tycho Brahe, the greatest observing astronomer of the sixteenth century, died in 1601, after some thirty years spent in collecting and recording data concerning the positions and movements of the heavenly bodies. The printing of his Progymnasmata was completed under the supervision of his great pupil, Johann Kepler, and the book was issued at Prague in 1602. A considerable part of the work had been printed by Tycho himself on his press at Uraniborg as early at 1588; but this book, entitled De Mundi Aetherei recentioribus Phaenomenis, had never been issued, although Tycho had sent copies to many of his friends and correspondents, including Digges and Dee.[394] The first opportunity that the world at large had to learn and study Tycho’s astronomical ideas and discoveries came with the publication of his Progymnasmata in 1602. Tycho’s reputation among those leading scientists who had been given the opportunity of following his work was so great that the lesser men eagerly studied his book when it appeared. Astronomers and compilers of almanacs made use of his observations and calculations long before Kepler, in 1627, published his Rudolphine Tables, based upon Tycho’s monumental labors.
There is no need to emphasize here the significance of Tycho Brahe in the history of astronomy, since his position as the most assiduous and systematic observer of the heavens before [221] the days of the telescope is universally recognized. Our concern is with his rejection of the Copernican theory and his proposing in its place a system which to his mind avoided the chief objections against both the Ptolemaic and the Copernican hypotheses. If judged solely by the proofs obtainable from direct observations of the stellar motions, Tycho’s system remained just as valid as that of Copernicus until the first measurements of stellar parallax were made in 1838.[395] There is little wonder, then, that as the Ptolemaic system became increasingly indefensible from the scientific point of view, the Tychonic system, which was scientifically tenable, was adopted as a middle ground by all scientists who were unwilling to accept the Copernican system in its entirety. The fact that the heliocentric theory rather than the Tychonic was finally enthroned upon the ruins of the Ptolemaic cosmology by the end of the seventeenth century was due solely to its proving more amenable to physical and mechanical explanations of the planetary motions and not to any confirmation by astronomical means. It required Newton’s mathematical demonstration of the movements and orbits of the planets in terms of his law of universal gravitation to eliminate Tycho’s system as one of two possible choices, each of them justifiable, and to leave Copernicus in undisputed command of the field.[396]
The enormous influence of Tycho’s system of the universe makes a clear understanding of its mathematical and astronomical relations to the Ptolemaic and Copernican theories indispensable to any genuine appraisal of seventeenth-century scientific thought. Tycho’s own observations contributed greatly to the overthrow of the old Aristotelio-Ptolemaic cosmology by destroying the doctrines of the solid spheres, the changeless heavens, and the distinction between the matter of the ethereal [222] and the sublunary regions. The great Danish astronomer also realized the immense mathematical superiority of Copernicus’ system, which recognized the intimate relationship of the sun to all the planetary orbits except that of the moon. On the other hand, Tycho shared the common Aristotelian belief that, if the earth moved, a stone dropped from a high tower would land very far to the west of the foot of the tower. The usual objections drawn from scriptural passages to the motion of the earth likewise had some influence with him. Far more important, however, were the immense distances and incredible sizes of the fixed stars—the inevitable mathematical consequences of the Copernican theory.[397]
The system proposed by Tycho preserved all the mathematical advantages resulting from Copernicus’ hypothesis, yet avoided its most serious disadvantages. He placed the earth immovable in the center of the universe, with the finite sphere of fixed stars, located just beyond the orbit of Saturn, rotating about the earth once every twenty-four hours. These details, however, were the only ones in the Ptolemaic system which he retained. The planets were not attached to solid orbs, but moved freely in the air or ether in accord with the laws of their nature. The moon circled about the earth, but all the other planets revolved about the sun. The latter, in its turn, revolved about the earth, carrying the planets with it. Because Mars, in opposition, approached nearer to the earth than the distance between the earth and the sun, the orbit of Mars was portrayed as intersecting the sun’s orbit about the earth—a supposition that would have been unthinkable in the ancient system of solid orbs.[398]
Nova Mvndani Systematis Hypotyposis
ab Authore nuper adinuenta, qua tum vetus illa Ptolemaica
redundantia & inconcinnitas, tum etiam recens Coperniana
in motu Terræ Physica absurditas, excluduntur,
omniaque Apparentiis Cœlestibus
apt:ßime corresponaent.
Fig. III.—Tycho Brahe’s Diagram of the Universe
From the second issue of the Progymnasmata (1610). This diagram first appeared in Tycho’s De Mundi Aetherei recentioribus Phaenomenis (1588).
A moment’s consideration of the geometrical principles involved will reveal that Tycho’s system was mathematically identical with that of Copernicus, and all computations of the positions of the planets were the same for the two systems.[399] The only relative motion involved was that of the earth with respect to the sun, or vice versa—it made no difference which way one chose to consider it. Tycho, therefore, freely adopted Copernicus’ figures for the relative dimensions of the solar system, making such slight corrections as his more accurate observations warranted. He assigned to the eighth sphere a thickness of 1,000 semidiameters of the earth, and placed it at a distance of from 13,000 to 14,000 semidiameters, whereas in the old astronomy its distance had been more than 20,000 semidiameters. His calculations for the sizes of the planets made Saturn 22 times as large as the earth, Jupiter 14 times, Mars 1/13 of the earth’s volume, Venus 1/6, and Mercury 1/19.[400] The fixed stars, because of the decreased distances and apparent diameters that he assigned to them, were computed by Tycho to be much smaller than the Arab astronomers had thought.[401] The smallest visible stars, instead of being considered 18 times as large as the earth, were calculated to be only 3/10 of the size of our terrestrial globe.
Tycho had first announced his system in his book of 1588, but this work, as we have seen, was distributed only to certain friends of the author and to a few eminent fellow scientists. Tycho had sent two copies to Thomas Savile in 1590, with the request that they be shown to Digges and Dee for their criticisms and suggestions.[402] The system was therefore known to the leading English scientists before it was regularly published as part of the Progymnasmata in 1602.
The results of Tycho Brahe’s investigations were quickly incorporated in the books of the English astronomical writers. The first decade of the seventeenth century also witnessed two other momentous contributions to the development of astronomy—the work of Kepler and Galileo. Their discoveries, [225] likewise, were eagerly followed, and immediately combined with the ideas of Gilbert and Tycho; thus all four of these authors left their stamp upon the English books on astronomy printed during the next few decades. It is important to understand the different ways in which the several contributions of these four men could be brought into harmony with the contending pictures of the structure of the universe. First, however, let us consider the discoveries themselves, and their relation to the astronomical research going on at the same time in England.
Kepler’s discovery and proof of the elliptical orbit of Mars was announced in his book, De Motibus stellae Martis, published in 1609. Galileo constructed his first telescope in the summer of 1609, and it was shown for the first time in public from the top of the Campanile in Venice in late August of that year.[403] This instrument was used only for terrestrial observations, and not until late that autumn did Galileo begin to examine the heavens with another and more powerful instrument he had constructed. His discovery of the satellites of Jupiter was made in 1610, and the first announcement to the world of these new facts of astronomy revealed by the telescope was made in his book, the Sidereus Nuncius. Galileo’s preface to this work is dated March 4, 1610, and the text records observations as late as March 2. The first copies were issued on March 13.[404] Galileo’s discovery of the rings of Saturn occurred after the publication of the book, and the sunspots were not noted by him until 1611.[405] The world first learned of the former through Kepler in 1611,[406] and the latter [226] were announced by Galileo in 1612, in the two editions of his Discorso . . . intorno alle Cose che stanno su l’Acqua.[407]
At the very period when Kepler and Galileo were making their significant contributions to the science of astronomy, Thomas Harriot and his friends and pupils were carrying on similar researches in England. Harriot, who had graduated B.A. from Oxford in 1579 and shortly thereafter had entered Sir Walter Ralegh’s service as his mathematical tutor, was one of the great mathematicians of the age. Captain John Davis, the famous navigator, in the dedication of his book, The Seamans Secrets,[408] to Lord Charles Howard, Baron Effingham, had named Harriot, along with Digges and Dee, as the three English scientists living in 1595 who could surpass all foreign rivals in knowledge and skill:
For I think there be many hundreds in England that can in a farre greater measure and more excellent methode expresse the noble art of Nauigation, and I am fully perswaded that our Countrie is not inferiour to any for men of rare knowledge, singular explication, and exquisite execution of Artes Mathematicke, for what Strangers may be cōpared with M. Thomas Digges Esquire, our Countryman the great Archmastric, and for Theoricall speculations to most cunning calculation, M. Dee and M. Thomas Heriotts are hardly to be matched: . . .[409]
Harriott’s place as a member of Ralegh’s circle of friends and as the leader in the scientific experiments and astronomical observations in which this group occasionally indulged was a matter of common knowledge among his contemporaries.[410] [227] Later, Henry Percy, ninth Earl of Northumberland, became the chief patron of Harriot, who resided at Sion, the Earl’s new seat near Isleworth, from about 1606 until his death in 1621.[411] He was the lifelong friend both of Ralegh and of the Earl, and well known to all their associates as a profound scholar and scientist. Harriot’s influence, therefore, was exerted through personal association rather than imparted through the medium of books. His A Briefe and true report of the new found land of Virginia (1588), an able geographical and economic survey of the region made while a member of Sir Walter Ralegh’s short-lived colony, was the only book by Harriot printed during his lifetime. The Artis Analyticae Praxis,[412] his great work on algebra, was edited by some of his friends and pupils and printed ten years after his death. Throughout his life Harriot’s friends constantly remonstrated with him for his failure to publish his scientific discoveries,[413] asserting that later men, because of this delay, were receiving credit for important innovations in which Harriot had actually anticipated them. Our knowledge of the scientific work of this outstanding English mathematician must therefore be derived solely from the manuscripts he left behind and from the letters of his friends.[414]
From Sir William Lower’s letter of February 6, 1610, we know that at this early date he was already observing the moon from his country seat in southern Wales with telescopes supplied by Harriot. At Harriot’s suggestion he was also studying Kepler’s book demonstrating the elliptical orbit of Mars, and finding such difficulty in mastering its complex mathematics that he wrote Harriot, begging him to elucidate some of the more troublesome details. In his letter answering Lower’s request Harriot also gave his friend an account of Galileo’s discoveries with the telescope, the latter’s Sidereus Nuncius having recently come to his hands. Lower, in his reply of June 21, 1610, acclaims the news in these enthusiastic terms:
Me thinkes my diligent Galileus hath done more in his three fold discouerie then Magellane in openinge the streightes to the South sea or the dutch men that weare eaten by beares in Noua Zembla. I am sure with more ease and saftie to him selfe and more pleasure to mee.[415]
Within little more than three months after the publication of the Sidereus Nuncius, therefore, Harriot had received and studied the book, had written an account of its contents to his friend Lower in Wales, and had heard from him in answer.
Many months before he knew of Galileo’s researches, Harriot was making observations with his own telescopes,[416] which were constructed by his mechanic Christopher Tooke under Harriot’s supervision.[417] In view of the earlier knowledge of the properties of lenses and the principles of the construction of the telescope which existed in England and was shared by Digges, Dee, Bourne, and doubtless many others, and the fact that Harriot took some sort of telescope with him on his expedition to Virginia in 1585, there is no reason for assuming that Harriot owed his telescopes to foreign inventors.
During the winter of 1609-10, Harriot had his friends and pupils observing the heavens with telescopes in various parts of England and sending him notes concerning their findings. This same group was also eagerly studying Kepler’s great work on the elliptical orbits of the planets within a few months of its publication. Harriot kept up a personal correspondence with Kepler on scientific subjects, and letters for the period from 1606 to 1609 have been preserved.[418]
There can be no question, therefore, that Harriot and his group of astronomers in England were not only fully abreast of all the latest developments in their science, but were also carrying on independent researches of their own along similar lines. Nor was this group an isolated one, unknown to contemporaries. Harriot’s connection with important political and literary figures, already touched upon, prevented the world from remaining ignorant of his circle’s unpublished investigations.
The influence of the discoveries made with the telescope tended, first of all, to give added support to the idea, suggested by Digges many years before and adopted by Gilbert, that the stars were not at a uniform distance from the center of the universe, but were infinite in number and scattered at varying distances throughout an infinite universe. The discovery of the moons revolving about Jupiter and of the phases of Venus and of Mercury similar to those of our moon made it seem probable, to those who reasoned by analogy, that the earth itself revolved about the sun in agreement with the hypothesis of Copernicus. Certainly the acceptance of these new revelations made the old Ptolemaic cosmology no longer tenable and left the Tychonic system as the only alternative to the Copernican.
The Tychonic system, unlike the old Ptolemaic system, could be reconciled with the new discoveries of Kepler and Galileo. Kepler’s demonstration of the elliptical orbits of the planets [230] about the sun was equally valid, whether the Copernican or the Tychonic plan was assumed. Kepler himself, for reasons connected with his acceptance of the Pythagorean belief that the sun was the noblest body and therefore most fit to occupy the center of the universe, was ever an ardent Copernican. Consequently, in spite of Tycho’s dying request to him that he demonstrate his theories according to the Tychonic rather than the Copernican system, Kepler proclaimed in his De Motibus stellae Martis[419] his belief in the heliocentric universe. In either system, however, the sun, not the earth, was the body which governed Mars’s orbit. The discoveries of the telescope, moreover, were not such as to make the Tychonic system absolutely untenable. The phases of Venus and Mercury, for example, were consistent with either hypothesis.
The Copernicans, of course, could reasonably maintain that the nature of the earth, as a body without light of its own, corresponded far more closely to that of the planets than to that of the sun, and hence there was greater probability that the earth circled about the sun than that the reverse was true. But this was the only important argument favoring Copernicus over Tycho; in other respects the findings of astronomers fitted either system equally well.
Particularly was this true of the modification of the Tychonic system to admit the rotation of the earth, which was the form most commonly accepted in England. As a simple and obvious variation which overcame the difficulty of assuming, as Tycho did, a tremendous speed of rotation for the primum mobile and the sphere of fixed stars, it would clearly appeal to all who were not convinced by the Aristotelian arguments against the earth’s rotation.[420] The freedom of English scientists from Aristotelian domination, together with Gilbert’s arguments drawn from magnetism to prove the earth’s rotation, [231] enabled the idea of terrestrial motion to become firmly established in England much earlier than on the Continent. The resulting picture of the universe was also consistent with a concept which had long been associated with the new astronomy in England—the belief in the infinite and varying distances of the stars.
The cosmological sections of Gilbert’s De Magnete exercised a profound influence upon Englishmen interested in science—an influence readily understandable in view of the state of astronomical thought at the time of its publication. Only a year after its appearance, Gilbert’s magnetical and cosmographical ideas had been seized upon by his countryman, Nicholas Hill, and used freely in proving the various propositions set forth in a little book expounding with intense enthusiasm Hill’s atomic philosophy.
Nicholas Hill, a citizen of London, entered the Merchant Taylors’ School in 1578, proceeded to St. John’s College, Oxford, in 1587, and became B.A. and a Fellow of his college in 1592. Anthony Wood tells us that Hill was for a time secretary to Edward De Vere, the famous Earl of Oxford, and that afterwards he lived under the patronage of Henry, Earl of Northumberland, sharing his philosophical studies.[421] Ben Jonson poked fun at Hill’s ideas in one of his epigrams, where he speaks of
. . . . . . . . those atomi ridiculous
Whereof old Democrite, and Hill Nicholas,
One said, the other swore, the world consists.[422]
Robert Burton, too, mentions Hill, referring to him in the Anatomy of Melancholy as one of the principal English supporters of the atomistic philosophy.[423]
Hill’s book was first published at Paris in 1601, and bore the title, Philosophia Epicurea, Democritiana, Theophrastica, [232] proposita simpliciter, non edocta. Another edition was printed at Geneva in 1619. The volume consisted of 509 philosophical propositions, covering many fields of scientific and metaphysical thought. These propositions show Hill not only as a follower of Democritus, but also as an ardent Copernican. In his twentieth proposition he states: “Omnis apparentia Coelestis, diurna, menstrua, annua, secularis, & periodica conuenientius, facilius, aptius per motum terrae suppositum, quam solis saluatur, & soluitur.”[424] That Gilbert’s ideas were of paramount influence in convincing Hill of the truth of the Copernican theory is made clear in Proposition 434, headed “Terrae Motum Sufficienter Probant” and containing in the margin, as authorities for the nineteen proofs that follow, the names: “Hermes, Cusanus, Nicetas, Copernicus, Nolanus, Gilbertus, Franciscus patricius.” Hill’s proofs are:
1. Magneticus confluxus grauissimorum. 2. Polorum magneticorum constantia & axeos. 3. Astrea terrae natura probabilis. 4. Φαινομένων explicatio optata. 5. Eccentricitatum mille absurditas sublata. 6. Continua generatio torporiferam quietem non admittens. 7. Aquarum terrae penè aequipōderantium motus manifestus. 8. Terrae in soluto & libero aethere suspēsio absque basi ad quietem necessaria. 9. Terrae animalitas, & primordialitas non sine motu locali intelligibilis, qui generalis rerum vita est. 10. Terrae figura admissa, demonstrata. 11. Terrae cohaerentia & firmitas. 12. Grauitatis nullitas praesertim rerum in proprijs locis existentium. 13. Improbabilis centri, & medij puncti infinitas. 14. Medij in mundo infinito nullitas. 15. Terrae tam exiguae impotentia continui solis ferendi. 16. Ignei solis dissipabilis substantia. 17. Naturae compendiosa perficiendi ratio. 18. Necessaria homogeneitas primarum & notabilium mundi partium. 19. Rotatio partium separatarum.[425]
The predominance of Gilbert’s magnetic discoveries in this list is instantly apparent. Moreover, Hill continues with a second list, of twelve items, headed, “Magneticam Terrae Naturam Satis Probant.”[426]
Quite different from Hill’s work was another book written under the immediate inspiration of Gilbert’s De Magnete, although not published until 1638, five years after its author’s [233] death. This was Francis Godwin’s The Man in the Moone: or a discourse of a Voyage thither by Domingo Gonsales.[427] Godwin (1562-1633) was Bishop of Llandaff, and later Bishop of Hereford. He is best known for his Catalogue of the Bishops of England[428] and his Rerum Anglicarum Henrico VIII, Edwardo VI, et Maria regnantibus, Annales.[429] The earliest possible date, from internal evidence, for the composition of his Man in the Moone is 1601. The cosmological passages must have been originally written before the announcement of Galileo’s telescopic discoveries in 1610, regardless of whether we accept or reject the possibility of later additions by Godwin to his manuscript.[430]
In Godwin’s story of a certain Spaniard, Domingo Gonsales, makes a journey to the moon by harnessing himself to a flock of specially trained geese, and after two years’ residence there returns to the earth and lands near Pekin. The descriptions of the lunar inhabitants do not concern us here, but the picture given of Gonsales’ journey through the heavens is of great interest as testimony to the influence of Gilbert’s cosmological ideas upon his contemporaries.[431] Godwin is [234] clearly trying to draw a reasonable and consistent scientific picture of what an observer might see and experience during a journey through the sky between the earth and the moon. Gonsales watches the earth rotate below him, and thus receives visual confirmation of that part of the Copernican theory. He takes occasion to refute from his own experiences the Aristotelian arguments denying the earth’s rotation, and inveighs against the wilfulness and blindness of the philosophers who will not admit the Copernican idea of the motion of the earth. He also vigorously denies the existence of the sphere of fire just below the moon.[432] He makes the point that the moon’s globe is a huge magnet like our earth but of less force because of its smaller size, and says that when he and his geese reached the point where the earth’s attraction was exactly balanced by that of the moon they stood poised in the heavens without any effort whatsoever, because they were then totally lacking in weight.[433]
Godwin, however, does not accept that part of the Copernican theory which portrays the earth as revolving about the sun,[434] refusing, like Gilbert, to take any definite stand on this point. All the cosmological ideas presented in The Man in the Moone are thus unmistakably derived from the De Magnete. Godwin merely gives an imaginative picture of the things his hero ought to observe during his journey through space if Gilbert’s theories of the universe were true. At every step he follows Gilbert with conscientious fidelity, and the text of his book shows no trace of ideas that were not current before the sensational telescopic discoveries of Galileo.
Turning back from fantasy to science, we may note, in passing, a curious book published in 1602 by Nathanael Torporley (1564-1632), a friend and pupil of Thomas Harriot and another member of that group of English mathematicians who received liberal aid from Henry, Earl of Northumberland. Torporley’s treatise, entitled Diclides Coelometricae seu Valuae Astronomicae Vniuersales,[435] expounds a simplified [235] spherical trigonometry designed for computing astronomical tables. The mathematical part of his work does not concern us here;[436] what is of interest is his belief that, in spite of the great importance of Copernicus’ theory, his system was in need of further perfecting. At the end of his book,[437] Torporley suggests a rather bizarre system of his own, in which each planet is placed at one extremity of a chord or lever, at the other end of which is a moving force which he calls the magade. The mechanical details of Torporley’s plan are wholly unsatisfactory, but they illustrate the prevailing eagerness to evolve some new physical explanation of the movements of the planets in their orbits.
After 1610, when the facts revealed by the telescope had become known, we find that these new astronomical data were at once combined with the earlier discoveries of Gilbert. The most interesting evidence of the use of Gilbert’s and Galileo’s findings to provide a tentative physical basis for the new astronomy is observed in Marke Ridley’s A Short Treatise of Magneticall Bodies and Motions,[438] published early in 1613. The engraved title-page of this book portrays, above the columns and arch which inclose the title itself, several scientific instruments, and the earth, the sun, and the planets, drawn to represent, so far as the space would permit, their relative sizes according to Tycho Brahe. Jupiter’s four satellites and two belonging to Saturn are portrayed. The sun, the earth, Jupiter, and Saturn have their axes of rotation indicated, and the phases of Venus and Mercury are suggested by shading their globes so that they have an illuminated crescent on the side toward the sun while the rest of their surfaces remains in shadow. Ridley explains this picture in his epistle to the reader:

Fig. IV.—Title-page of Ridley’s Book on Magnetism (1613)
[237]In this place I thinke good to aduertise thee as concerning the magnitude of the seuen Planets, with their respect vnto the earth, out of Ticho Brahe, described in the top of the Title Page; that whereas their proportion cannot be set forth truly in any types, being at too great oddes; therefore I haue deciphered that in figures; as let the Earth be but one part, the Sunnes greatnesse will be 140 times so much; Saturnes 22, Iupiters 14. And if that Venus haue 6 parts, the Earth will haue 37 parts, if Mars be one part, the Earth is 13, if Mercury be one part, the Earth is 18, if the Moone be one part, the Earth will continue her 42 times. Besides, I haue drawne the Axis in the greater Planets, as being bodies Magneticall: for I trust that these following times will discouer whether they be paralell one to the other, or no, as also what naturall motions else they haue, because that Astra natant, auis instar in aëre, aut piscis in vnda, and here it might be sayd that we hope that many new points in Philosophy and Astronomy will blossome and spring out of this kind of learning hereafter.[439]
Ridley’s first chapter, in which he attempts a universal definition of magnetism, gives significant testimony concerning the way in which the English scientists were hoping, by a wider application of Gilbert’s discoveries and theories, to find a physical explanation of all the planetary motions:
That we define to be a Magneticall body, which seated in the aether or aire, doth remaine and place it selfe in one place or kind of situation naturall, not alterable; as all starres do, and the great regent Globes of Saturne, Mars, Iupiter, the Sunne and the Earth do; or such as with respect and attendance follow other Globes, as the two starres which support Saturne, the foure attenders vpon Iupiter, lately discouered by the trunke spectacle, the two trauesers [sic] about the Sunne, called Venus and Mercury, and lastly the Moone, which doth follow, or go about the Earth, and respecteth the same alwayes with one pole: and therefore hath a peculiar Magneticall vertue that guideth her in this kinde of situation.[440]
Ridley makes no mention of Galileo, so that we cannot be sure whether his information concerning the new astronomical facts revealed by the telescope was derived directly from the Italian scientist’s works or from similar investigations being carried on by the group of English astronomers. Some of the discoveries, such as the rotation of the sun about its axis, for [238] which he suggests magnetical explanations had been first published only a year before his book was issued. Furthermore, Ridley himself made observations with the telescope, according to his adversary, William Barlowe.[441]
Marke Ridley was one of the most eminent physicians of his day. As a Cambridge man (B.A., 1580; M.A., 1584) who had been resident at the university at the time of the Ramus controversy, his independent attitude toward scientific problems, and his desire to find a new explanation of the physical world—an explanation whose details could be verified by observation and experiment—probably dated from his university days. After spending several years in Russia as physician not only to the English merchants resident there but also to the Czar Boris Godunoff, he returned to England in 1598 and, from 1607 until his death in 1624, held many important posts in the College of Physicians. Between 1616 and 1618 he was engaged in a bitter controversy on magnetical subjects with William Barlowe, Archdeacon of Salisbury, another writer on magnetism. The dispute centered about Gilbert’s magnetic explanation of the motion of the earth and Ridley’s extension of it to include the new phenomena brought to light by the telescope.
Barlowe’s book, entitled Magneticall Aduertisements,[442] was printed in 1616, although the author claimed it had been written in 1609 and presented in manuscript to Sir Thomas Challenor. He insinuated that this manuscript had fallen into Ridley’s hands, and that the latter had made use of it in his book of 1613.[443]
Barlowe’s book is in many respects an English epitome of Gilbert’s De Magnete, with the histories of the erroneous opinions of ancient authorities and their refutations omitted, and with some supplementary matters of Barlowe’s own invention introduced.[444] Barlowe maintains that he had begun [239] his own magnetical investigations twenty years before Gilbert’s book appeared, and had communicated many of his observations to the author of the De Magnete. As evidence for his co-operation with Gilbert and the friendly relations between them, he publishes a letter Gilbert wrote to him shortly after the De Magnete had been issued, requesting some of Barlowe’s experiments which he wished to print, with due credit, in an appendix to the De Magnete, so “that you may be knowen for an augmenter of that act.”[445]
In spite of his respect for Gilbert and his own skilful experiments with the properties of magnets, Barlowe vehemently rejected the conclusions concerning the rotation of the earth which had been set forth in the sixth book of the De Magnete:
But concerning his sixth Booke entreating of the motion of the earth, I thinke there is no man liuing farther from beleeuing it, than my selfe, being nothing at all perswaded there vnto, by the reasons of other men, which he alledgeth, and as little or lesse (if it were possible) by those his inventions, endeuoring to proue the motion of the earth by the earthes Magneticall force and vertue.[446]
Barlowe might have made out a very good case for his rejection of Gilbert’s conclusions by showing that they were based upon insufficient evidence and therefore not scientifically acceptable until further experimental confirmation could be produced. Instead, as a devout churchman, he relied almost wholly upon an appeal to the Scriptures and banned all further consideration of the hypothesis of the earth’s rotation because it was contrary to revealed truth as embodied in the biblical texts.
This intolerant attitude toward Gilbert’s fruitful theories, in addition to the personal accusations of plagiarism, caused Ridley to enter the fray with a pamphlet entitled Magneticall Animadversions . . . Vpon certaine Magneticall Advertisements . . . from Maister William Barlow.[447] In this book he made the countercharge that Barlowe had plagiarized from his own [240] Treatise of Magneticall Bodies and Motions, and reasserted the theory of the earth’s motion due to its magnetic force. He denied the validity of Barlowe’s arguments from the Scriptures and suggested several passages that might be quoted favoring the earth’s motion. He went even farther, and accused Barlowe of failing to live up to his declaration that he would readily forsake Aristotle to embrace the truth, saying:
These things I haue set downe, not hoping to perswade you any whit, or others who are to much adicted to that they sucked from their youth out of Philosophers, which all Schollers read after they haue beene two yeares in the Vniuersities, especially from their old friend Aristotle, whom you say you would forsake to embrace the truth, and though many things of great moment in him of Philosophic and Anotomy were confuted demonstratiuely by Galen long since, yet because all read the first, and very few the latter, but onely professors in Physicke, so that his opinions are almost imbraced by all, yet now in these daies, where dies Diem docet, by the multitude of the writings and labours of late most learned Writers, it is come to bee an vsuall assertion in the Schooles that, in Anatomicis & Astronomies errauit Aristoteles; and certainely if wee shall obserue and ponder what a thing the wonderfull vastnesse of expansion, the fine and thin Firmament hath, and what a great distance there is betweene the earth and the farthest limits (for Spheres are but fained) of the aduancement of Saturne from the earth, but especially of the fixed Starres, which are held to be remoued as farre againe and much mooue[448] from Saturne, it might be said, that the earth firmed in her position might mooue her whole bodie many thousand miles from place to place, and yet there would bee found no excentri[ci]tie of the fixed starres by the earth, and all those arguments which are vsed by Aristotle, Ptolomie, Regiomontamis, Iohannes de Sacrobosco and others to proue, that the earth is centrum vniuersi would bee no otherwise, then now they are, for the earth is not centrum vniuersi, but is as it were pūctum insensibile respectu vniuersi & stellarum fixarum, and no doubt but that Copernicus and Tichobrahe most perfect and exact Astronomers, who make the Sunne to be centrum vniuersi & planetarum accompted the said arguments and proofes to be of force, and as truely verified of the Sunne, as of the earth if a man might passe thether to trie the same, . . .[449]
Ridley’s clear statements concerning the way in which most [241] of Aristotle’s scientific doctrines had been disproved and completely abandoned by the leading English scientists of the early seventeenth century are fully corroborated by the facts we have brought to light during the course of this survey of astronomical thought. They should be placed beside Bacon’s assertions regarding the dominance of Aristotelianism, in order to give a clearer picture of the truth. The new telescopic discoveries, incidentally, were not ignored in the universities. In 1611 one of the questions set forth for disputation in the Comitia by the incepting Masters at Oxford was, “An luna sit habitabilis?”[450] This was only a year after Galileo’s book had brought that question to the fore.
In 1618 Barlowe published a rejoinder to Ridley, entitled A Briefe Discouery of the Idle Animaduersions of Marke Ridley . . . vpon a Treatise entituled, Magneticall Aduertisements.[451] Again he charged Ridley with stealing from his book passages he did not understand, and ridiculed the latter’s presumption in applying magnetic principles to the theories of stellar motions.
But that mine Animaduersors magneticall skill is ascended vp into our Moone it selfe; yea, and yet higher, farre beyond the Moone, vnto the other Planets and Starres, and into euery one of them, this is such a point of his Magneticall Philosophie, that would make Stupidity it selfe astonished to heare of it. . . .
It seemeth that mine Animaduersor endeauoureth for to make shew, that he hath a stranger gift; namely, that by his very lookes (for his lookes, with his Truncke-spectacle, are his meanes) he can turne all things to be Magneticall, that hee doth earnestly behold; He hath scowred the Heauens already, euen from the one end vnto the other, that both Planets and Stars are become magneticall in his head; what tumultuous stirre may they breed there, no man can tell, it is his safest way to confine his Magnetismes vnto the earth, as their naturall seat, and not suffer them to clamber vp into the skies, where they haue nothing to doe, lest that infinite dispersion of his magneticall knowledge, doe in the end ouercharge his braine, and make him magnetically mad . . .[452]
Instead of pressing the point that Ridley was engaging in speculations based upon insufficient knowledge, Barlowe resorted to ridicule and to the literal interpretation of the Scriptures as the main bulwarks of his case. He also brought forward the old and now quite ineffectual accusation of despising Aristotle,[453] and reasserted the idea that the supposed motion of the earth could only be considered as a mathematical hypothesis for simplifying astronomical calculations.[454]
In his discussion of the arguments advanced by the advocates of the earth’s rotation as a substitute for the inconceivably swift rotation of the eighth sphere postulated by the Aristotelians, Barlowe makes a most significant comment which reveals his recognition of the extent to which the new ideas were finding support among the mechanicians and skilled artisans. He says:
But although such [arguments] as these are, may goe current in a mechanicall Trades-man shop, yet they are very insufficient to bee allowed for good, by men of learning, and Christians by profession, who know right well, that it is great folly for to oppose that which we call difficult, vnto an omnipotent power, Who stretcheth out the heauens like a curtaine, and spreadeth them out as a tent to dwell in, Esay 40. ve. 22. He stretcheth out the North ouer the empty, and hangeth the earth upon nothing, &c. Iob 26. ver. 7.[455]
The controversy between Ridley and Barlowe attracted sufficient attention, at the time, to find an echo fourteen years later in a passing allusion in Ben Jonson’s play, The Magnetick Lady.[456] Barlowe, however, was definitely on the losing side and his partisans were dwindling in numbers, so that soon only the fundamentalist theologians could be depended upon to hold firm against the new astronomical ideas. At the very moment of his quarrel with Ridley, the mechanicians were, by his own admission, on the side of his opponent.
Comparable with the instant acceptance and elaboration by English scientists of current magnetic and telescopic research was the immediate use which the poet, John Donne, made of [243] the new scientific ideas. Donne’s frequent references in his poems to contemporary astronomy, and his use, in his poetic figures of speech, of concepts derived from its recent theories and discoveries, are matters which have been noted by almost every student of Donne and therefore need not be dwelt upon here.[457] More significant than the mere fact of the presence of these allusions is the nature of the knowledge they indicate, and the date at which they appear. The famous Dean of St. Paul’s was an able and intelligent student of science, capable of at least a passable understanding of the mathematical basis of the new theories and of the precise nature and value of the various scientific arguments favoring both the old and the new doctrines. Though not a scientist himself, science had been one of the subjects to which he had applied his intensely eager and active mind, and he was probably more learned in that field than any of his literary contemporaries except Gabriel Harvey.
It is not surprising, therefore, that his allusions and images drawn from science are generally precise, rather than vague, and based now upon the old, and now upon the new, theories, depending upon his poetic purpose. It is natural, also, that he should have ardently followed the progress of astronomy. The discoveries of Kepler and Galileo were scarcely published before they were used by Donne as material for his writing.
The most significant work of Donne’s dealing with the new astronomy is Ignatius his Conclaue,[458] published less than [244] a year after Galileo’s Sidereus Nuncius and not long after Kepler’s De Motibus stellae Martis. Both of these astronomers and their recent works are mentioned. Most interesting, however, is the session in hell before Satan and Loyola, in which Copernicus presents his claims to be admitted to the inner circle of those who “had so attempted any innouation in this life, that they gave an affront to all antiquitie, and induced doubts, and anxieties, and scruples, and after, a libertie of beleeuing what they would; at length established opinions, directly contrary to all established before.”[459] After the author of the De revolutionibus has stated his case, Loyola demands:
But for you, what new thing have you inuented, by which our Lucifer gets any thing? What cares hee whether the earth trauell, or stand still? Hath your raising vp of the earth into heauen, brought men to that confidence, that they build new towers or threaten God againe? Or do they out of this notion of the earth conclude, that there is no hell, or deny the punishment of sin? Do not men beleeue? do they not liue iust, as they did before? Besides, this detracts from the dignity of your learning, and derogates from your right and title of comming to this place, that those opinions of yours may very well be true. If therefore any man haue honour or title to this place in this matter, it belongs wholly to our Clauius, who opposed himselfe opportunely against you, and the truth, which at that time was creeping into euery mans minde.[460]
As an indication of the immediate influence of the new astronomical discoveries on English literature, this little work by one of the chief poets of the period is of outstanding importance. It also shows that Donne, when he considered the Copernican astronomy from the scientific point of view, was in complete agreement with the thought of the leading English scientists in suggesting that that system was probably much closer to the truth than the ancient system based upon Ptolemy and Aristotle.
Francis Bacon, even more than Donne, has been given a prominent place in almost every discussion of the state of science in the early seventeenth century. Yet the philosopher was certainly less familiar than the poet with the progress of astronomy in his own day. The two works by Bacon that deal with the science of the stellar motions are his Descriptio Globi Intellectualis and his Thema Coeli. Though written about 1612, shortly after he had become aware of the new telescopic discoveries, they were not printed until many years after his death. Thus they had little opportunity to influence contemporary astronomical thought, and are significant merely as illustrations of Bacon’s knowledge of cosmological science and speculation.
Concerning the scientific merits of those works and the extent of Bacon’s acquaintance with astronomy, there is little that needs to be added to the excellent discussion by Robert Leslie Ellis in his preface to the Descriptio Globi Intellectualis.[461] It will suffice here to emphasize that Bacon was relatively ignorant of some of the elementary details of astronomy, and unaware of much of the data, both ancient and contemporary, concerning the mathematical phases of the science of the planetary motions. For example, he knew nothing of Kepler’s laws regarding the orbits of the planets, although he knew of Galileo’s work because of the sensation which the telescope’s revelations had created throughout Europe, and had a general knowledge of the systems of Tycho Brahe and Copernicus.
Bacon’s writings on astronomy, therefore, present that haphazard combination of sound, rational comment, on the one hand, and mistaken assumption and egregious blunder, on the other, which one so often finds when a highly intelligent author attempts to write profoundly upon a subject of which he has only a superficial knowledge.[462] Bacon’s analysis, in the [246] Descriptio Globi Intellectualis, of the systems of astronomy that had been proposed up to his time, like his skeptical attitude toward the claims of all theoretical systems, is for the most part penetrating and pertinent, even if in minor points it reveals its author’s insufficient acquaintance with the details of his subject. But when, in the Thema Coeli, Bacon suggests another system of his own, his complete ignorance of the fundamental problems of astronomy becomes glaringly evident. His system is the ancient one, dating back to pre-Aristotelian times, wherein the planets move in undefined spiral paths in the same direction as the firmament, but at a slower pace. Every effort to revive this system in the past had failed completely. The moment any thorough student of astronomy had tried to make it account for any stellar motions except the few which were simplest and most obvious, its utter worthlessness had become evident. Alpetragius had revived it in the twelfth century, and Aquinas had at first been inclined to adopt it, until a little study in practical astronomy had proved to him that it was totally inadequate.[463] Telesio and his followers, none of whom were well versed in astronomy, had again put it forward in the sixteenth century, and Bacon, learning of it from their books, had, with his lack of knowledge, accepted it as a plausible doctrine.[464]
As an example of the superficial science of the Telesians, from whose books Bacon drew so many of his astronomical ideas, Patrizzi’s arguments in favor of the possibility that the earth was flat might be cited. Patrizzi maintained, among other things, that the varying altitude of the stars as the observer moved north or south was no proof of the earth’s sphericity, because these altitudes would vary even if the earth were flat. Two of Bacon’s own contemporaries among English scientists, Robert Hues[465] and Nathanael [247] Carpenter,[466] had demolished this naïve argument by pointing out that it was not the mere variation in altitude, but the exact manner of variation, that furnished conclusive mathematical proof that the earth was a globe.
The scientific skepticism which Telesio, Patrizzi, and, above all, Bacon, proclaimed was commendable in spirit and often an invaluable corrective to blind adherence to outworn scientific doctrines. When it arose, however, from mere ignorance of the fundamental problems of the science criticized, it lost all merit and became, if heeded, a hindrance to real scientific progress. Far more fruitful for the advancement of science than the indiscriminate distrust of all systems is that critical attitude of mind which examines in detail the merits of each system, and accepts, rejects, or withholds judgment upon each point after a thoroughly sound and intelligent investigation.
In 1614 John Barclay, in his Icon Animorum, described the characteristics of the inhabitants of the various nations of Europe. Speaking of the attitude of the English toward the mathematical sciences, he said:
But in Philosophy, and the Mathematicks, in Geography, and Astronomy, there is noe opinion soe prodigious and strange, but in that Island was eyther inuented, or has found many followers, and subtile maintainers, but such as through taedious disputations cannot plainely state the question, which they would seeme to vphold: That the Earth is mooued round, and not the Heauens: that the Sunne, with the Planets, and all the other Starrs are not mooued in their globes caelestiall; there are no such globes at all; and lastly, whatsoeuer any doating Philosopher hath heretofore broached, some of them do either hold, or would seeme to do: as if then they were more deeply wise then common men, when they neglect and slight the ordinary wisdome as poore and low, and search deeper into the secrets of Nature, which few are able to apprehend.[467]
Barclay’s singling out the English nation for this satiric comment is invaluable testimony to the widespread popular interest in the new scientific ideas, and to the greater prevalence in England of a spirit favorable to the overthrow of the Aristotelian cosmology. His censures, be it noted, apply equally to the Copernicans and to the supporters of that modification of Tycho’s system upheld by the followers of Gilbert’s magnetic philosophy. These two rival systems, which jointly dominated the astronomical thought of the first half of the seventeenth [249] century,[468] were at one in denying the solid spheres, the immutable heavens, the distinction between the ethereal and the sublunary regions, and in proclaiming the earth’s rotation and the sun’s central position with respect to at least five planetary orbits.
The rapid decline in England of the Aristotelio-Ptolemaic astronomy is attested by almost every discussion of the science of the heavens that was penned after the beginning of the seventeenth century. Even in works by theological writers and in the cheap popular handbooks, many of the old doctrines are openly abandoned. For example, the traditional figures of Alfraganus for the dimensions of the heavenly bodies and the celestial spheres are gradually supplanted by new figures derived from Copernicus and Tycho. These two moderns, with Gilbert and Galileo, become the authorities cited, instead of Aristotle, Ptolemy, and the Arab astronomers.
The progress of Copernicus and Tycho and the downfall of Aristotle and Ptolemy are nowhere better illustrated than in the popular almanacs. There we are dealing with books that sold for a penny or two and were bought and read by even the lowest classes among the literate population. These annual almanacs were tiny octavos of twenty-four leaves at most, containing the calendar for one year, with the position of the moon for each day, notations of the favorable and unfavorable days for purging, planting, bathing, bloodletting, and the like, followed by prognostications for the four seasons and the twelve months.[469] Other miscellaneous information was often included, such as the dates and significance of the eclipses due to occur that year, a schedule of the fairs throughout England, and the times of beginning of the law terms. Most [250] almanacs of the sixteenth and seventeenth centuries followed the same conventional pattern, but several of the abler compilers were in the habit of including a page or two presenting the elementary facts of astronomy according to the accepted authorities. In these pages they usually imparted such bits of knowledge as the size of the earth and the various planets, the number and sizes of the stars in the heavens, and the dimensions of the planetary orbits.
Apparently the earliest of the compilers of annual almanacs who proclaimed themselves ardent supporters of the Copernican theory were Edward Gresham and Thomas Bretnor, who published almanacs during the first two decades of the seventeenth century.[470] They were two of the most noted, and likewise the most learned, among the almanac makers and astrologers of the early years of King James’s reign. Ben Jonson refers to them in his play, The Diuell is an Asse, acted in 1616:
I, they doe, now, name Bretnor, as before
They talk’d of Gresham, and of Doctor Fore-man,
Francklin, and Fiske, and Sauory (he was in too) . . .[471]
Gresham’s almanacs prove him an outright Copernican. In his prognostication for 1604, he opens his prediction for spring with the sentence: “The Spring is then said to begin when the Sunne is retired to that point of his thwarting path-way, that mooueth on the worlds poles, or rather where this earthlie orbe maketh his diurnall circumuolution to such a point of the [251] Sunnes surface as appeareth equidistant the sayde poles.”[472] Similar statements introduce his prophecies for the other seasons of this and later years.
In the second decade of the seventeenth century, if we are to judge from the references in contemporary dramatists, whenever an Englishman thought of an almanac he thought of Thomas Bretnor. Bretnor’s name is equated to “almanac” in Middleton and Rowley’s A Faire Quarrell (1617),[473] and in Middleton’s Inner Temple Masque (1619).[474] He is unquestionably the person whom the author of Act IV, Scene ii, of The Bloody Brother had in mind when he gave the name of Norbrett to his astrologer.[475]
However severely the dramatists might satirize Bretnor as the most prominent astrologer of his day, his scientific contemporaries continued to respect him for his learning. William Bedwell, in the preface to his Kalendarium viatorium generale (1614), makes a point of excepting Bretnor and three others from his censure of the horde of common almanac makers, saying: “I speake not of Hoptons, Mathewes, Rudstones, Bretnors, and such like learned ones: but of such, who beside certaine Fustian, as they call it, strange and barbarous termes, (ampullas, et sexquipedalia verba) haue nothing worth the reading.”[476]
Though firmly believing in the utility of the science of astronomy for the astrological predicting of future events, Bretnor was neither quack nor impostor, but a man of genuine ability and one deeply versed in the mathematical sciences, [252] which he taught in “English, Latine, French, & Spanish.”[477] He numbered among his friends Arthur Hopton and Edmund Gunter, the third professor of astronomy at Gresham College.[478] He was in the habit, in his books, of advising his readers concerning the best scientific works published in England during the preceding year. His almanac for 1617, for instance,[479] announced the publication of Edward Wright’s translation of Napier’s book on logarithms, while in 1618[480] “Bretnor recommended to his readers Aaron Rathborne’s The Surveyor,[481] Napier’s Rabdologiae,[482] and Ridley’s Magneticall Animadversions. In a previous year he had called attention to Ridley’s book on magnetical bodies and motions, but Barlowe’s works received no praise. Instead, they were completely ignored by Bretnor.
Such a man was clearly no ignorant almanac-maker, but one whose writings had authority among the learned as well as among the multitude. It is significant, therefore, that in Bretnor’s almanacs we find the most rabid Copernicanism of the age. Their author outdoes Gilbert in his contempt for the upholders of the old theories. In the almanacs he issued annually from 1605 to 1618 he never missed an opportunity to ridicule the old astronomy and to proclaim his adherence to the Copernican theory. His introductions to the prognostications for each of the four quarters of the year—a typical feature of the almanacs of the period—always give the beginnings of the seasons according to the Copernican hypothesis, with scornful allusions to the older ideas as “the vulgar opinion,” “the old fantasie,” or the “old dotage.” The prognostication for “Winter” in the almanac for 1615 is characteristic:
This Brumal season, commonly called Winter, and vsually taken for the first quarter of our Astronomicall yeare, tooke its begining the 11 of December last: for then (according to old dotage) did the [253] Sun enter the first scruple of the cold and melancholicke signe Capricorne, or rather according to verity this earthy planet entring the first minute of Cancer, and furthest deflected from the Sunnes perpendicular raies, did then receiue least portion of Sunshine, and greatest quantitie of shadow.[483]
Bretnor even went so far as to revise the usual astrological figures to make them correspond to the Copernican theory, changing, for example, “the sun in Aries” to read, “the earth in Libra.”[484]
Bretnor’s friend, Arthur Hopton, wavered between the traditional astronomy and the Tychonic system, but tended toward the latter, and consistently adopted the new calculations of both Copernicus and Tycho. In 1612 he published a perpetual almanac and handbook of miscellaneous information, entitled A Concordancy of Yeares.[485] In his preface Hopton remarks upon the popularity of such books as Digges’s Prognostication euerlasting and the Kalender of Shepeherdes, but says that their astronomical tables of the motion of the sun and moon are out of date and badly in need of correction. For that reason he has undertaken to prepare and publish this new general almanac. John Selden contributed a short encomiastic poem, in Latin, in praise of Hopton, wherein he recited a list of ancient astronomical writers of Britain who lent luster to their native land by their scientific learning. Selden’s fourteen lines are printed upon three pages, at the beginning of Hopton’s book,[486] completely engulfed by learned notes upon the persons Selden has mentioned. His array of great English astronomers begins with semilegendary figures among the ancient Britons and comes down to the fourteenth century, including Bede, Grosseteste, Roger Bacon, and Richard Suiseth. Selden’s notes contain much [254] interesting information concerning these men, and defend Bacon against the vulgar charge of being a magician, mentioning in this connection “that great Clarke M. I. Dee” who long since had promised a defense of Bacon against these accusations.[487]
Hopton’s book remained in use for many years, and as late as 1639 we find references to his Concordancy of Yeares and Digges’s Prognostication euerlasting as the two most familiar works of this type.[488] The brief epitome of astronomy which Hopton gives at the beginning of this book is therefore of particular significance because of its wide circulation. He expounds the geocentric system, but with constant references to Tycho Brahe. In his discussions of the sizes of the planets and of their orbits, he gives the old figures of Alfraganus, but places beside them the modern computations of the great Danish astronomer. Then, in a separate chapter, he explains Tycho’s methods of determining these figures, sets them forth once more in greater detail, and clearly indicates his preference for the modern calculations.[489] In the series of annual almanacs which Hopton issued from 1606 to 1614, Copernicus and Tycho are frequently mentioned, and their figures consistently employed.
Hopton was in close touch with the science of his day, and, like Bretnor, numbered many of the leaders in this field among his personal friends. In his almanac for 1614,[490] after mentioning Gilbert’s work on magnetism, he calls his readers’ attention to the recent work on the subject by his friend, Marke Ridley, [255] and recommends his book, entitled A Short Treatise of Magneticall Bodies and Motions.
Two very able treatises on surveying were also published by Hopton. The preface to one of them contains a most interesting discussion of the relation between ancient and modern learning, in which Hopton takes the reasonable, fair-minded attitude that had been characteristic of the English scientists who had preceded him:
But happily some will say, if there were sufficient instrumēts before, then what needeth these new inuentions? would wee haue our owne wits more excellent then our predecessors? Of such and such like, I familiarly enquire if Antiquity bee onely Mistresse of this faculty, if moderne wits may intimate or exhibite nought vnto the world; if we must only beleeue what is set downe, without contradiction; should that be so, how farre had this age beene from the perfect Idea of the Art, whose excellency turneth euery heart after the same as the Heliotropion after the Sun? into what an intricate Laborinth of cōfused errors had we run? The most ancient Philosophers were as contrary in their sects, as erronious in their opiniōs, till time brought in Truth, truth Knowledge, and Knowledge perfect Vnderstanding, what a nūber of sects had we? . . . But shaking off the old differēces, enquire of the commodity of the Compasses, Sea-cards, and new Maps, & of many other deuises & engines, that haue beene lately set forth more beneficial then any heretofore, of which the old Philosophers & Mathematicians were ignorant of & I think if they were liuing, they would reioyce to see, as amongst many I will remember G. Frisius Astrolabe, the Mater wherof being excellent and a most Art-like proiectment resembling the true lineaments of the spheare, and is now made perpetually famous with the Edition of the Rete, by our ingenious countriman M. I. Blagraue. But my Pen shall not bee so much dismeasured to reproue ancient men, to the end to draw the glory to them that be present. Had we liued then we had knowne lesse then they, and were they liuing now, they would know more than we: euery thing hath his time, before it come to maturity: neither doth nature alot like time to euery like action.[491]
Hopton introduced the practice of citing Copernicus and Tycho as his chief authorities and giving the dimensions of the [256] solar system and its members according to their calculations. His lead was followed by almost every subsequent almanac maker who included such astronomical data. The new figures supplant the old in the almanacs of Philip Ranger,[492] Sofford,[493] George Hawkins,[494] Thomas Turner,[495] Mathew Pierce,[496] and Thomas Langley.[497] William Frost not only gives Tycho’s figures for the sizes of the stars and planets, but vigorously defends his following of the moderns instead of Ptolemy, Alfraganus, and Albategnius. He warmly praises Tycho’s system, and criticizes that of Copernicus because the great distance between Saturn and the fixed stars marred its symmetry.[498]
Of special interest is the short treatise “Of Astronomie in generall” which Walter Strof included in his almanacs. It contains high praise for Tycho, and the system it expounds is wholly Tychonic. Strof was not inclined to accept the Gilbert modification of this system so popular among English astronomers. He says:
Solide Orbes and Comets in the sublunary region, how haue they been mayntayned by many, both elder and later, which yet by the infallible obseruations and instruments of Tycho (a man borne for the good of posterity, and indued with a spirit of purpose to inuestigate truth) hath beene found altogether false. To say nothing of that great question, whether the Heauens or the Earth do in very deed moue, which yet I am out of doubt may be proued to be in the Heauens, but here is no place for such a discourse. Many other things haue beene found out from the grounds and Hypothesis of the euer-honored [257] Tycho: as that Venus and Mercury mooue about the Sun; that all the other Planets, except the Moone, respect the Sun for their Centre.[499]
Eustace Clarke was another author who gave the dimensions of the planets and their orbits according to Tycho’s Copernican figures. He also mentioned the increase in astronomical knowledge brought about by the telescope:
The number of fixed Starres is commonly defined 1725, although their number cannot indeed be exactly limited; being almost infinite, as Astronomers do easily descrie, by the help of an hollow instrument the invention of Galilaeus: By the said instrument Venus is discerned with the eie, increasing and decreasing as the Moon. Saturne is seen having 3 bodies; Jupiter having 4 other Starres moving with him for his attending Guard: likewise the Sunne himselfe appeareth diversly spotted as the Moon &.[500]
Another almanac maker of the period, Dove, devoted the whole of five pages to an exposition of the Tychonic system, and printed a diagram of the universe according to Tycho.[501] For further information he referred his readers to John Swan’s Speculum Mundi, “lately printed.”[502]
The compilers of almanacs, however, were not the only ones who realized that the progress of astronomical investigation had made it necessary to revise the usual elementary expositions of the facts about the heavens. These short astronomical treatises, constantly reappearing as popular handbooks or as chapters in encyclopedic philosophical works, had since the Middle Ages followed a conventional pattern, differing only in the number and variety of ancient authorities cited. In the seventeenth century, however, even devout and conservative clergymen felt [258] that the old models failed to provide an adequate treatment of so important a subject. Modern science could no longer be ignored, and wise men, they believed, should seek to reconcile it with the essential tenets of the Christian religion rather than blindly to oppose the new discoveries which reasonable men were coming more and more to accept.
Such was the attitude of Samuel Purchas, Hakluyt’s successor as the collector and editor of materials dealing with colonial enterprise and voyages of discovery. In 1613 he published his first work, entitled Purchas his Pilgrimage. Or Relations of the World and the Religions Observed in All Ages.[503] In the first edition, the second chapter of the first book is devoted to an account of the creation of the world, based almost entirely upon the first chapter of Genesis and the commentaries thereon by the early Church Fathers. Since Purchas was a clergyman, the biblical approach to the question had been natural. On the other hand, he had graduated from St. John’s College, Cambridge, the society which contributed such an amazing proportion of the leaders of the scientific movement in England, and had dedicated himself to the task of chronicling the new geographical discoveries. It is therefore not surprising that when he enlarged this first work of his for the second edition, published in 1614, he greatly augmented his account of the Creation in order to bring in a discussion of both the ancient and the modern scientific theories.
In the augmented version, Purchas divided his description into six parts, or “days,” following the practice of Du Bartas and of other Renaissance encyclopedists who had treated the question from a point of view primarily religious and philosophical. He emphasized the conflicting scientific theories of the Creation advanced by ancient and modern philosophers, and the uncertainty of human knowledge in such matters. At the same time he displayed an acquaintance with the most recent ideas and discoveries of Tycho Brahe, Gilbert, and Galileo, and a definite desire to show that there was no essential conflict [259] between the latest findings of science and the account of the Creation given by Moses. Tycho Brahe’s ideas particularly appealed to him. As for Galileo, he pointed out that the telescope’s revelation of vast multitudes of stars hitherto unseen accorded perfectly with the Bible:
They [the ancient and modern astronomers] agree not in the order of the Planets, nor how many semi-diameters of the earth the heauen is eleuated, which after Ptolemys Hypotheses are 20000. after Tychos reckoning 14000. Hence it is, that the quantitie and the swiftnesse is much more after the former, then after this later opinion, which doth better salue the incrediblenesse thereof, then faining a Giant-like labor (as Ramus calleth it) of the earths continuall rolling.
The number of the starres some haue reckoned 1600. others 1022. and Tycho Brahe more. Galileus his glasse hath made them innumerable, in descrying infinite numbers otherwise not visible to vs, and especially the Galaxia full of them. Yea God himselfe propounds it to Abraham (whom Iosephus cals a great Astronomer) as a thing impossible to number them. It is his owne royall prerogatiue, he counteth the number of the starres, and bringeth out their armies by number, and calleth them all by their names.[504]
Purchas’ discussion of the early theories of planetary motions in connection with Galileo’s discoveries is also worth noting:
Diuersitie of motions caused the auncients to number eight Orbes; Ptolemie on that ground numbred nine; Alphonsus and Tebitius ten; Copernicus finding another motion, reuiued the opinion of Aristarchus Samius of the earths mouing, &c. Others which therein dissent from him, yet in respect of that fourth motion haue added an eleuenth Orbe, which the Diuines make vp euen twelue by their Empyreall immoueable heauen. And many denie this assertion of Orbes, supposing them to haue beene supposed rather for instructions sake then for any reall being. And Moses here saith expansum, as Dauid also calleth it a Curtaine, which in such diuersitie of Orbs should rather haue beene spoken in the plurall number. The Siderius Nuncius of Galilaeus Galilaeus tells vs of foure new Planets, Iupiters attendants, obserued by the helpe of his Glasse, which would multiply the number of Orbes further. A better Glasse, or neerer sight and site [260] might perhaps finde more Orbes, and thus should wee runne in Orbem in a circular endlesse maze of opinions. But I will not dispute this question, or take it away by auerring the Starres animated, or else moued by Intelligentiae. A learned ignorance shall better content me, and for these varieties of motions, I will with Lactantius, ascribe them to God the Architect of Nature and co-worker therewith by wayes Natu[r]all, but best knowne to himselfe.[505]
Purchas was by no means the only divine of the period who, unlike William Barlowe, was a supporter of the new astronomy rather than its bitter and uncompromising opponent. Francis Godwin, the author of The Man in the Moone, has already been mentioned. Nathanael Carpenter, John Swan, and John Wilkins, the authors of the three most widely read discussions of the new astronomy printed in the second quarter of the seventeenth century, were all of them clergymen.[506] The fact that so many churchmen were among the open and ardent supporters of the new astronomical doctrines of Copernicus, Gilbert, Tycho, and Galileo doubtless helped greatly in counteracting the impression that these modern beliefs were unorthodox. It contributed also to the gradual weakening of the scientific authority of the encyclopedic works on natural philosophy which had been the product of an earlier age but retained their popularity with seventeenth-century readers. The best-known and most influential of these books designed to summarize man’s knowledge of the divinely created universe was Du Bartas’ Divine Weekes, which has been discussed in an earlier chapter. A prose encyclopedia, composed by Du Bartas’ fellow countryman, Pierre de la Primaudaye, at about the same time as his own poem, was second in importance. This great encyclopedia, entitled L’Académie Françoise, consisted of four parts, devoted respectively to moral philosophy, the “body and soule of man” (the microcosm), the “description of the whole world” (the macrocosm), and “Christian philosophy.”[507] Only [261] the third part, first published in Paris in 1580 and translated into English in 1601, has to do with cosmology.[508] Its extensive discussion of astronomical doctrines is along purely traditional lines, uninfluenced by the Copernican hypothesis or by the discoveries relating to the new star of 1572. The early Church Fathers are quoted at great length, and several sections are devoted to the customary refutation of Aristotle’s idea of the eternity of the world. An epitome of this conventional sort of theological exposition of astronomy was what Purchas had originally prefixed to his Pilgrimage, only to feel impelled later to change it so as to include the modern theories and discoveries.
Less open-minded theologians than Purchas were equally conscious of the inadequacies of the ancient arguments employed by sixteenth-century writers like Du Bartas and La Primaudaye. The text of the Scriptures was still the mainstay of these divines in their battle against the new cosmology; but for scientific proof they no longer turned confidently to Aristotle, but sought new reasons for affirming the rotation of the heavens and the immobility of the earth.
The most interesting and revealing of the religious and philosophical works of this period which aimed to epitomize the traditional natural philosophy was Thomas Tymme’s A Dialogue Philosophicall Wherein Natures Secret Closet Is Opened, and the cause of all motion in Nature shewed out of Matter and Forme.[509] Tymme displayed a better understanding of his subject than the average author of this type, and wrote excellent English prose, but in spirit he belonged more truly to the age of Du Bartas and La Primaudaye. He was already an old man when he wrote this book in 1612,[510] so he answered the [262] clear statement of some of the reasons advanced in support of the Copernican theory by having the other party to his dialogue bring forward the favorite charge of conservative old age: the folly of preferring novelty to antiquity.[511] The certainty of divine philosophy, Tymme asserted, was far better than the deceitful arguments derived from human philosophy, and he proceeded to bring forth the usual array of scriptural passages to prove the earth’s immobility and the motion of the heavens.[512] Yet, for his final argument, he turned to scientific demonstration, and, surprisingly enough, brought forward, not the usual Aristotelian reasons that we would expect, but “a memorable Modell and Patterne, representing the motion of the Heauens about the fixed earth, made by Art in the immitation of Nature, by a Gentleman of Holland, named Cornelius Drebble, which instrument is perpetually in motion, without the meanes of Steele, Springs, & Waights.”[513]
The machine Tymme refers to is the famous perpetuum mobile of the noted Dutch inventor, Cornelis Drebbel. A model of this machine—a kind of air-thermometer, which depended for its action on the expansion and contraction of a certain quantity of air or gas under varying temperatures and pressures—was constructed by Drebbel for King James, and set up at Eltham Palace sometime between 1606 and 1608.[514] It became one of the most popular curiosities of the day. Tymme’s description of this instrument, together with the drawing of it that he printed, reveals that the model at Eltham was designed with a number of refinements so as to make it a sort of perpetually moving celestial globe. The principle of its action was only vaguely understood by Tymme, but he definitely implies that, in the “fierie spirit,” mixed with “his proper Aire” which caused the motion of this machine, we have an illustration [263] of the physical causes which produce the movements in the heavens.[515] Strangely enough, Drebbel himself was a supporter of Copernicus;[516] yet he gave to at least one Englishman a new physical argument for the ancient system, which could be opposed to Gilbert’s magnetic explanation of the rival hypothesis of the earth’s rotation.
Turning from the almanac makers and the religious writers to the scientific workers, we find that Gresham College was, throughout the first half of the seventeenth century, a general clearinghouse for information concerning the latest scientific discoveries. Its professors of astronomy and geometry were among the ablest scientists of their day, and the college’s central location in London made their rooms a convenient rendezvous for all those who were actually contributing to the advancement of science in England. The gatherings of scientists at Gresham did not originate with the meetings described by Wallis as taking place in 1645,[517] but had been occurring for nearly half a century. The foundation of the Royal Society in 1662 was thus the culmination of a movement, dating back to the reign of Queen Elizabeth, in which Gresham College had by long custom been the meeting place of a group of Englishmen actively interested in scientific investigation.
We have already observed how John Dee and his friends constituted a sort of scientific academy during the first half of Elizabeth’s reign. At the end of the sixteenth century the English scientists, most of whom were then working in or near London, kept themselves accurately informed concerning the progress of each other’s investigations and contributed suggestions—and even important sections and additions—to their friends’ works.[518] The establishment of Gresham College [264] in 1597 and Briggs’s election as the first professor of geometry made his rooms there a convenient center for the interchange of the latest information on scientific subjects. Groups of scientists gathered at Gresham to discuss recent developments; and, because the lectures at the college were widely patronized by the skilled artisans, expert mechanics, and navigators for whose instruction they had been founded, the Gresham professors were always in close touch with the practical workers in many fields of applied science.[519] Both learned men and artisans brought books they had written which dealt with the mathematical sciences, and submitted them for examination and criticism by the Gresham Professor and his friends. Many witnesses attest the value of this exchange of ideas, and the helpfulness of Briggs and his group in assisting the authors of worthy books and urging the publication of their works.[520]
Among the most significant proofs of the part the Gresham professors played in bringing scientific men together is one found in a little pamphlet by William Oughtred (1575-1660), entitled The just Apologie of Wil: Oughtred, against the slaunderous insimulations of Richard Delamain, in a Pamphlet called Grammelogia, or the Mathematicall Ring (1633).[521] Oughtred was one of the most noted English mathematicians of the seventeenth century. Throughout the last fifty years of his life he was rector of Albury, near Guilford in Surrey, and came up to London but once each year, as a rule. In this pamphlet he describes the visit he made in 1618:
In the Spring 1618 I being at London went to see my honoured friend Master Henry Briggs at Gresham Colledge: who then brought me acquainted with Master Gunter lately chosen Astronomie reader there, and was at that time in Doctour Brooks his chamber. With whom falling into speech about his quadrant, I shewed him my Horizontall Instrument: He viewed it very heedfully: and questioned about the projecture and use thereof, often saying these words, it is a very good one. And not long after he delivered to Master Briggs to be sent to me mine owne Instrument printed off from one cut in brasse: which afterwards I understood he presented to the right Honourable the Earle of Bridgewater, and in his booke of the Sector printed sixe yeares after, among other projections he setteth down this.[522]
It is worth noting that Oughtred, writing nearly fifteen years after his visit, gives the erroneous impression that in 1618 [266] Gunter was already Gresham Professor of Astronomy. Gunter was not elected until March 6, 1619, yet in 1618 Oughtred found him staying temporarily at Gresham College and occupying the rooms of the Professor of Divinity.
The roll of the Gresham College professors of geometry and astronomy during the period we are considering includes several of the most eminent men of their age in those fields. The chair of geometry was filled by Henry Briggs from 1597 to 1619, by Peter Turner from 1620 to 1630, and by John Greaves from 1630 to 1643. The astronomy professors were Edward Brerewood (1597 to 1613), Thomas Williams (1613 to 1619), Edmund Gunter (1619 to 1626), Henry Gellibrand (1626 to 1636), Samuel Foster (1636 to 1637 and 1641 to 1652), and Mungo Murray (1637 to 1641). In 1645 Gresham College, as we know, was the meeting place of the group of scientists which later formed the nucleus of the Royal Society. These gatherings were probably held in the rooms of Samuel Foster, whom Wallis mentions as one of the leaders.[523]
So famous was Gresham College, in later times, as the center of the scientific activity of the early seventeenth century, that John Ward, writing in 1740, had to correct the mistakes of others in making nearly every scientist of that period a Gresham professor. Robert Hues,[524] Richard Norwood,[525] John [267] Blagrave, William Gilbert, and Edward Wright were among the scientists erroneously assigned to Gresham College. There was some excuse for this error, for these men were the friends, and in some cases the collaborators, of actual professors in Gresham College. All of them were doubtless in the habit of meeting at the college for the discussion of matters relating to science.
None of the published works of these Gresham College professors had any direct connection with the controversy between the old astronomy and the new. Briggs’s books dealt with mathematics, and his great service lay in his work in introducing the use of logarithms and calculating the tables with the number ten as a base. In this task he was aided by Edward Wright and Edmund Gunter. The latter not only helped to prepare the logarithmic tables of trigonometric functions, but devised improvements in many astronomical instruments, and shared with Oughtred the honor of inventing the logarithmic slide rule.[526] Gellibrand was the first to discover the secular variation of the earth’s magnetic poles.
Even if the Gresham professors and their associates published no books dealing directly with the question of the true system of the universe, their teaching would inevitably involve some reference to that problem. By means of their public lectures and their personal discussions with their numerous friends and pupils, their ideas were transmitted by the spoken word to a large audience among their countrymen. Thus their opinions would exert no little influence upon contemporary thought.
There can be no doubt that most of the Gresham professors of astronomy and geometry were outright Copernicans, though [268] some may have given favorable consideration to Tycho’s system. As able mathematicians who rejected the older tables of planetary motions and unanimously adopted the figures of Copernicus and Tycho, their casting aside of the old Ptolemaic system is implicit in all their scientific writings. In the case of Henry Briggs we have direct evidence of his acceptance of the Copernican system. It is to be found in a communication he sent to George Hakewill, the author of An Apologie or Declaration of the Power and Prouidence of God In the Gouernment of the World,[527] a significant document in the famous literary quarrel between the ancients and the moderns. In the second edition of this work, published in 1630, Hakewill inserted “a briefe view of the most observable inventiōs of moderne Mathematicians vnknowne to the Ancients sent mee from my learned friend Mr. Brigges Professour of Geometrie at Oxford.” The first item in Briggs’s list of “Mathematica ab antiquis minus cognita” is the Copernican system, and reads as follows:
Astronomia Copernicana quae docet Terram esse centrum orbis Lunaris, Solem vero esse centrum reliquorum omnium planetarum: quod in Venere & Mercurio, cum sint in inferiori parte suorum orbiū etiam oculis deprehendi potest, ope tubi Optici nuper inventi. Docet etiam per motum Telluris diurnum, Ortus & Occasus omnium syderum: Et per motum ejusdem annuum in Orbe suo magno, omnium Planetarum motus & distantias, eorumque in caelo progressus stationes & regressus, multo facilius & accuratius investigare, quàm per Ptolomaei aut antiqui cujusquam Epicyclos aut alias Hypotheses.[528]
Other items in Briggs’s list are: Galileo’s discovery of the satellites of Jupiter, and the development of algebra, of logarithms, and of trigonometry.
That Henry Gellibrand, also, was an adherent of the Copernican theory is clearly proved by the reference to Copernicus in his preface to Wells’s Sciographia[529] and by the appendix on longitude that he added to The Strange and Dangerous Voyage of Captaine Thomas Iames.[530] Even clearer are the statements [269] in the most famous of Gellibrand’s scientific works, A Discourse Mathematical on the Variation of the Magneticall Needle. Together with Its admirable Diminution lately discovered.[531] At the end of this book, which describes the experiments by means of which he discovered that the magnetic variation was not constant at any one place but underwent a cyclical change, the author states:
I will not here enter into a dispute concerning the cause of this sensible diminution, whether it may be imputed to the Magnet, or the Earth, or both. It is not unknowne to the world, how the Greatest Masters of Astronomie, which this age hath afforded, for the more easy salving the apparent anomalar motions of the fixed and erratique caelestiall lights, and avoyding that supervacaneous furniture of the Ancients, do with all alacrity embrace that admirable Copernicean Hypothesis of the diurnal, Annual, & Secular motions of the earth, in so much as conferring with that Great Astronomer D. Phil. Lansberg in Zealand about Astronomicall matters, did most seriously affirme unto me, he should never be disswaded from that Truth. This which he was pleased to stile a truth, I should readily receive as an Hypothesis, and so be easily led on to the consideration of the imbecillity of Mans apprehension, as not able rightly to conceive of this admirable opifice of God or frame of the world, without falling foule on so great an absurdity. Yet sure I am, it is a probable inducement to shake a wavering understanding.[532]
Gellibrand goes on to mention Galileo’s report of Cesare Marsili’s tract containing the assertion that a slow, but continual, shift in the meridian line had been observed. If this shift be true, says Gellibrand, it may “open a faire way for the salving of that Irregular Motion imputed to the Axis of the Earth.”[533] He refers here to the motion that Copernicus assigned to the earth’s axis in order to account for the alterable obliquity of the ecliptic. Here again, in Gellibrand’s book, we find one more example of an English scientist ever on the alert to discover some new physical principle which would explain the motions that Copernicus attributed to the earth.
More than two decades after the establishment of Gresham College, two new professorships in the mathematical sciences [270] were created in England. In 1619 Sir Henry Savile founded the first professorships of astronomy and geometry at the University of Oxford and brought about a marked revival in scientific scholarship there. One specific provision of his statutes was that the professor of astronomy, in addition to lecturing on the Almagest of Ptolemy, must also present in their proper places the newer theories of Copernicus and other recent astronomers.[534] If we remember that a mastery of the mathematics of the Almagest was, until the time of Newton, the necessary foundation of mathematical astronomy for Copernicans as well as for the adherents of the old cosmology, we shall not make the mistake of thinking that Henry Savile was trying to maintain the old theories simply because he required Ptolemy’s book to be used as the basis for the exposition of the newer hypotheses.
Henry Briggs left Gresham College to become the first Savilian Professor of Geometry, and many of the later professors at Oxford were drawn from the ranks of the “third university of England.”[535] Briggs’s colleague as the first professor of astronomy was John Bainbridge, who in 1618 had published a very able book recording his observations of the comet of that year. This treatise, entitled An Astronomicall Description of the late Comet,[536] proves that Bainbridge was fully acquainted with the work of Gilbert, Tycho Brahe, Kepler, and Galileo, and that he was a zealous advocate of the new astronomy against the traditional ideas of the Aristotelians. He used a telescope in making his observations,[537] and took pains to give his reader a definite hint that he favored the heliocentric hypothesis over all rival theories:
[271]These considerations [concerning the orbit of the comet] bee onely fit for those who haue beene rapt vp aboue the elementary regions of vulgar Schooles: and slept not in Parnassus, but Olympus, vnder the spangled canopy of Vrania; I can hardly keepe within the sphaere of this little Treatise, and scarsely refraine from the Samian Philosophy of Aristarchus in the earths motion, were it not I feared another Aristarchus his broach: and that I must reserue these mysteries for a more learned language.[538]
Bainbridge, later in the book, engaged in a spirited attack upon the Aristotelians, ridiculing their doctrines concerning comets and their theory of the solid orbs:
I haue at large shewed the Comets places as they appeared in the surface of Heauen, . . . but there is another place of more difficult inquisition, and greater admiration, and that is the Comets distance from this our habitable Orbe.
Common schooles treading the wrie steps of that great and witty, but often mis-leading Peripateticke, would confine this, and other Comets within the higher region of the aire; neither could his palpable error in the place of Galaxia (or the milkie-way in Heauen) acknowledged by most bring them into suspition of the like deuiation from the high aetheriall region of Comets into the Elementary vallies of Meteors; where, and with whom to place this Comet were to hide so glorious a candle vnder a bushell, and not to set it in a candlesticke, that all in the house may see; to set a beacon not on an hill, but in a dale, especially if wee consider that the highest region of the aire (by the Optickes demonstration from the time of twilight) is not many aboue 50. english miles from the earth. . . .
The analogie also obserued in the starres betwixt their distance from the earth, and their motion about the same, doth eleuate this Comet aboue the Lunary regions, his proper motion being scarse at any time the fourth part of hers.
This argument was sometimes accounted a firme demonstration, before that conglomeration of solide orbes was with the Aries or engines of Astronomicall obseruations battered and demolished: neither is it yet reiected by those who well deserue the first place in the restauration of this celestiall Art; for though those Babylonian wals be ruinated, yet is the analogie of motion and distance stil preserued. It was the saying of diuine Plato, . . . God is the great Master of Geometrie, hauing created all things in waight, measure, and number, as holy writ doth witnesse.[539]
One of Bainbridge’s contemporaries at Oxford was Robert Burton, author of the famous Anatomy of Melancholy. Burton made no contribution of his own to astronomical thought, but his encyclopedic work contains invaluable summaries of the opinions of others. His practice was to quote the various ideas of all the authorities whose books he had read, without any consistent attempt to decide between them. His Anatomy of Melancholy, consequently, gives an excellent cross section of all the works available to the seventeenth-century scholar, and his familiarity with the writings of the leading English scientists is of special interest to us. His book does not deal primarily with the mathematical sciences, so that references to the men discussed in this study would not normally appear. However, in his chapter entitled “Air rectified, With a digression of Air,”[540] he discourses upon the astronomy of his age, mentioning most of the noted writers in that field, from Copernicus to Kepler and Galileo. In listing the earnest supporters of the Copernican theory, he never fails to include his own countryman, Thomas Digges.[541] John Dee is also cited in the same discussion,[542] as well as Marke Ridley’s work on magnetism. In his preface, also, Burton mentions both Digges and Gilbert, saying:
Copernicus, Atlas his successor, is of opinion the earth is a planet, moves and shines to others, as the moon doth to us. Digges, Gilbert, Keplerus, Origanus, and others, defend this hypothesis of his in sober sadness, and [hold] that the moon is inhabited.[543]
Burton’s knowledge of Digges’s ideas was gleaned both from the Alae seu Scalae Mathematicae and from the treatise on the Copernican system appended to the Prognostication euerlastinge. A copy of the former work was among the books Burton left to Christ Church, Oxford, in his will.[544] In the Anatomy of Melancholy he quotes from Digges’s [273] Prognostication,[545] apparently from memory, since he substitutes the word “studio” for “labore.” It is certain, therefore, that he was familiar with the work.
Other books in Burton’s own library are worthy of notice. Not only did he have the first editions of the works of Copernicus and Reinhold and copies of the books by several of the later continental astronomers, but he also had a large collection of the writings of the English scientists we have been discussing. Besides Digges’s books, he owned volumes by Dee, Hood, Blundeville, Gunter, and Bainbridge.[546]
Another of Bainbridge’s contemporaries at Oxford was Nathanael Carpenter (1589-1628?), a Fellow of Exeter College and, although a Doctor of Divinity, a bitter opponent of Aristotelian natural philosophy. A book of his attacking the doctrines of the Aristotelians, entitled Philosophia libera, was published at Frankfort in 1621. A second edition was printed in England in 1622.[547] In his preface to this edition, Carpenter, in common with nearly every scientific writer in England, takes pains to make a clear distinction between Aristotle himself and his blind and bigoted followers who violently maintained his infallibility in matters of science. The author’s censures are directed almost wholly against this latter group, whom Aristotle would disown, he says, were he alive today. Carpenter has respect for Aristotle’s genuine contribution to science, but scorn for those who denied the necessity for critically examining all the Stagirite’s theories and rejecting his many erroneous doctrines.[548]
In the Philosophia Libera Carpenter attacks most of the traditional Aristotelian conceptions of the heavens. He adopts Gilbert’s idea that the earth is a huge magnet, and argues in favor of the rotation of the earth due to its magnetic properties.[549] Though setting forth with much intelligence and fairness the arguments both for and against the Copernican theory, he indicates a preference for Tycho’s system, modified to include belief in the earth’s rotation.[550] He prints (on page 389) a diagram of the Tychonic plan of the universe.
In 1625 Carpenter published his learned textbook of geography—the most extensive and best-known treatise in English on that science that was issued during the first half of the seventeenth century.[551] Ten years later a second edition of this thick quarto volume appeared. Carpenter devoted the first half of his book to an exposition of astronomy, and the second half to a treatise on geography.
The astronomical sections of Carpenter’s Geography merely paraphrase and expand in English the ideas previously set forth in the Philosophia Libera. The author considers at great length the various theories of the earth’s motion. He accepts Gilbert’s theory of terrestrial magnetism as a physical proof of the rotation of the earth, and defends this idea with many spirited arguments.[552] Like Gilbert, he ridicules the contentions of the Aristotelians against the rotation of the earth, and sides wholly with Copernicus in all points touching that part of his hypothesis. He also embarks on a detailed refutation of the theologians who maintain that the earth’s motion is contradicted by the Scriptures.[553]
As in his earlier work, Carpenter, at the end of his discussion of the rival systems, indicates his preference for the modified [275] form of the Tychonic system as a “middle way” between “Ptolomies stability of the Earth, and Copernicus his three Motions.”[554] He explains this system at some length,[555] modestly defending his boldness in passing by the systems of Ptolemy, Copernicus, and Tycho Brahe in favor of one different from all three, and stating that he justifies it “no farther than will stand with Astronomicall observation.”[556]
Carpenter’s book was the most important scientific treatise on astronomy in English that was published in the second quarter of the seventeenth century. Next in order was a work which, though inferior scientifically, may have reached an even wider popular audience. This was the Speculum Mundi of John Swan, printed at Cambridge in 1635, and again in 1643, 1665, and 1670. Nothing definite is known of the author except that he was a minister and a Master of Arts of Cambridge University. His book is a typical Renaissance encyclopedia of knowledge. It is divided into six sections, corresponding to the six days of the Creation. The author intended it to be a prose Du Bartas, and he frequently quotes the French poet in Sylvester’s translation. The tone, spirit, and contents of the book are decidedly conservative, and even reactionary, where disputes involving scriptural texts are concerned.
Considering the aim and the models of the Speculum Mundi, we might reasonably expect its cosmological teachings to be identical with those of Du Bartas or of The French Academie of La Primaudaye. There are many striking differences, however, which provide a significant index to the changes in astronomical thought which had taken place since the beginning of the seventeenth century. Even the most conservative encyclopedist, unless he were willing to ignore completely the scientific discoveries of recent decades, could no longer maintain the old cosmology. The Aristotelio-Ptolemaic system was now completely discredited wherever any pretense was made to up-to-date scientific knowledge, and intelligent conservatives and “fundamentalists” who could not swallow the [276] Copernican theory were earnest supporters of the Tychonic system.
Nowhere is this better illustrated than by John Swan in the cosmological sections of his Speculum Mundi. In two different parts of the book, he gives lengthy refutations of the Aristotelian doctrines of the changeless heavens and the distinction between the matter of the sublunary region and the purer fifth element of which the heavens were supposedly composed. He shows that he is fully aware that the researches of astronomers had proved that the new star of 1572 and all subsequent novae and comets were far above the moon, and that the idea of solid orbs was therefore completely demolished:
Those indeed who follow Aristotle, make them [the heavens] of a Quint-essence altogether differing from things compounded of the Elements: But for mine own part more easily should I be perswaded to think that there is no such fifth essence in them, but rather that they are of a like nature with the Elements, or not much differing.
For first, although Aristotle deny any change or alteration to have been observed or seen in the heavens since the beginning of the world; yet he was deceived: For Hipparchus, who had better skill in Astronomie then ever Aristotle had, he (as Plinie witnesseth) telleth us out of his own diligent and frequent observations that the heavens have had changes in them; for there was in his dayes a new starre like unto that which was once in Cassiopea. . . .
What great difference then can there be between the heavens and things here below, seeing in their own natures both of them do tend to corruption, and are subject to mutation? . . .
But besides all this, the observations of our best and modern Astronomers make much against him: for they have modestly and manifestly proved, that not onely new starres, but comets also have been farre above the moon. As for example, that strange starre which once was at the back of Cassiopea’s chair, was of an extraordinarie height above it; for it shined without any difference of Aspect, Parallax, or diversitie of sight, even untill all the matter whereof it consisted was consumed; . . .
Neither was it this starre alone, but others also after it, even Comets themselves, whose places were found to be above the moon: for observing more diligently and exactly then in former times, the observers could easily demonstrate this truth also: thinking thereupon that many of those Comets which have been seen in former ages were burnt out, even in the starrie heaven it self, and not so many of them below the moon, as generally (without serious observation) have [277] been supposed. . . . And now what of all this? Nothing but onely thus: viz. If Comets be burnt, consumed and wasted in the starrie heavens, it seemeth that there is no great difference between them and things here below.[557]
In another passage, Swan gives a detailed history of many of the new stars and comets observed by Tycho, Kepler, and others, and reaffirms the same conclusions.[558] For religious reasons, however, he rejects the idea of the earth’s motion. The arguments he gives are the traditional ones of the Aristotelians and the theologians.[559] They reveal the author’s lack of any real scientific training and prove him to be merely the recorder of the conservative opinion of his day. Nevertheless, when, in his account of the fourth day’s work, Swan discusses the sizes of the planets, he uses the modern figures of Tycho Brahe instead of the ancient ones of Alfraganus. He also definitely adopts Tycho’s system of the universe and inserts a diagram of that system,[560] pointing out at the same time how it disproves the older theories of the solid orbs.[561]
The Speculum Mundi represents the conservative opinion of the period. The blindly intolerant reactionaries who sought to reassert the inviolability of Aristotle’s natural philosophy, without either understanding that philosophy or the basis of the criticisms launched against it, found a zealous champion in Alexander Ross (1591-1654), the Scottish master of Southampton Grammar School. Ross was a prolific writer on all subjects, religious or philosophical, and the self-elected champion of Aristotle, and the Aristotelian interpretation of scriptural texts, against all innovators both ancient and modern. His arguments opposing the new scientific ideas revealed a complete ignorance, not only of the elementary principles on which all science is founded, but also of the essential features of the very theories he was attacking. They closely resembled in character the speeches made in the legislatures of certain [278] southern states not many years ago, advocating the passage of bills to prohibit the teaching of the doctrine of evolution.
Ross first entered the lists against the new cosmology in 1634 with a book attacking the ideas of Nathanael Carpenter and of Philip Lansberg, an eminent continental writer on astronomy who was an ardent adherent of the Copernican theory.[562] The sort of arguments that Ross employed had nothing to do with the scientific points at issue, and to anyone with a knowledge of astronomy, whether he accepted the Copernican theory or not, the book clearly proved Ross’s incompetence to discuss the subject on any intelligent or reasonable grounds. His diatribe, however, carried the sort of threat that is always at the command of fundamentalist demagogues of his type. It might readily deceive and inflame others who were as ignorant as Ross himself was of the fundamental concepts of both the old and the new science of astronomy. To counteract the obscurantist vituperation of Ross, John Wilkins, then a young man of twenty-six, wrote A Discourse concerning a New Planet: Tending to prove, That ’tis probable our Earth is one of the Planets. This book was published in the same volume with the third edition of his The Discovery of a World in the Moone. The engraved title-page for the entire book portrayed the figures of Copernicus, Galileo, and Kepler. Above them was a diagram of the heliocentric system, with the stars placed at varying distances beyond the orbit of Saturn, just as in the well-known diagram by Thomas Digges which had first appeared sixty-four years earlier.[563]
Wilkins’ Discourse concerning a New Planet replies point by point to Ross and to other opponents of the new astronomy. [279] It gives a clear presentation of the reasons for considering the Copernican system the most probable one, showing how it gives a better explanation of the observed facts of astronomy than any of the rival systems, including Tycho Brahe’s. By an intelligent appeal to reason and common sense, Wilkins attempts to demonstrate the absurdity of most of the arguments advanced by the adversaries of the heliocentric system, pointing out how many of Ross’s statements betray a complete ignorance of the demonstrable truths of physics and astronomy. He says:
’Tis considerable, that amongst the followers of Copernicus, there are scarce any, who were not formerly against him; and such, as at first, had been thoroughly seasoned with the Principles of Aristotle; in which, for the most part, they have no lesse skil, than those who are so violent in the defence of them. Whereas on the contrary, there are very few to bee found amongst the followers of Aristotle and Ptolomy, that have read any thing in Copernicus, or doe fully understand the Grounds of his opinion; and I thinke, not any, who having been once setled with any strong assent on this side, that have afterwards revolted from it. Now if we do but seriously weigh with our selves, that so many ingenious, considering men, should reject that opinion which they were nursed up in, and which is generally approved as the truth; and that, for the embracing of such a Paradox as is condemned in Schooles, and commonly cryed downe, as being absurd and ridiculous; I say, if a man doe but well consider all this, he must needs conclude, that there is some strong evidence for it to bee found out by examination; and that in all probabilitie, this is the righter side.
’Tis probable, that most of those Authors who have opposed this opinion, since it hath bin confirmed by new discoveries, were stirred up thereunto by some of these 3 insufficient grounds.
1 An over-fond and partial conceit of their proper inventions. . . . [In this class Wilkins lists Tycho Brahe, whose opposition to Copernicus he attributes to the desire to exalt his own rival system; also Carpenter and Origanus, whose systems followed Tycho’s except that they adopted Gilbert’s idea of the rotation of the earth due to its magnetic force.]
2 A servile and superstitious feare of derogation from the authoritie of the antients, or opposing that meaning of Scripture phrases; wherein the supposed infallible Church, hath for a long time understood them. . . .
[280]3 A iudging of things by sence, rather than by discourse and reason: a tying of the meaning of Scripture, to the letter of it; and from thence concluding Philosophicall points, together with an ignorance of all those grounds and probabilities in Astronomie, upon which this opinion is bottomed. And this in all likelihood, is the reason why some men, who in other things perhaps are able Schollers, doe write so vehemently against it: and why the common people in generall doe cry it downe, as being absurd and ridiculous. Vnder this head I might referre the opposition of Mr. Fuller, Al. Ross, &c.
But now, no prejudice that may arise from the bare authoritie of such enemies as these, will be liable to sway the judgement of an indifferent considering man; . . .[564]
Not all of Wilkins’ arguments in favor of the Copernican theory would stand the test of modern scientific scrutiny. They were, however, well designed to appeal to his contemporaries. He makes use, for example, of the traditional idea that the planets were arranged in a harmonious manner so that their periods of revolution increased with their distance from the center of the universe, and points out that under this theory the immense distance between Saturn and the fixed stars postulated by Copernicus becomes much more probable than the contrary hypothesis:
Wee usually judge the bignesse of the higher Orbs, by their different motions. As because Saturne finishes his course in thirty yeares, and Iupiter in twelve, therefore we attribute unto those Orbes such a different proportion in their bignesse. Now if by this rule wee would finde out the quantitie of the eighth Sphaere, wee shall discerne it to be farre neerer unto that bignesse, which Copernicus supposeth it to have, than that which Ptolomy, Tycho, and others, ordinarily ascribe unto it. For the starry Heaven (say they) do’s not finish his course under 26000 yeares; whereas Saturne, which is next unto it, do’s compasse his Orbe in thirty yeares. From whence it will probably follow, that there is a very great distance betwixt these in place, because they have such different termes of their revolutions.[565]
Wilkins shows a familiarity with the works of Copernicus, Tycho Brahe, Galileo, and Kepler, and acknowledges his special indebtedness to the last for many of the points brought out in [281] his own discourse.[566] Alexander Ross, however, was not an adversary to be silenced by reason or by the authority of anyone except the infallible Aristotle. With the hardihood of those zealots who are wholly unconscious of their own ignorance, he undertook to demolish the ideas of almost every important figure in seventeenth-century thought. Wilkins, Carpenter, Lansberg, and Copernicus were not his only victims. With equal aplomb he dispatched Galen, Sir Thomas Browne, William Harvey, Galileo, Francis Bacon, Sir Kenelm Digby, and Thomas Hobbes.[567] Therefore it is not surprising that he should produce a lengthy rejoinder to Wilkins. This book has a title in Ross’s typical style: The New Planet no Planet: or, The Earth no wandring Star: Except in the wandring heads of Galileans. Here Out of the Principles of Divinity, Philosophy, Astronomy, Reason, and Sense, the Earth’s immobility is asserted; the true sense of Scripture in this point, cleared; the Fathers and Philosophers vindicated; . . . and Copernicus his Opinion, as erroneous, ridiculous, and impious, fully refuted.[568]
The author’s preface to this book furnishes ample proof of the utter confusion in his mind regarding the actual details of the new astronomical theories:
The title of this new book is a may be (that the Earth may be a Planet) but I say that may not be: For a Planet is a wandring starre, [282] and the Earth is not a starre in its essence, nor a wanderer in its motion, And indeed you wrong our common mother, who so many thousand yeares hath been so quiet and stable, that now she should become a wanderer in her old age; but if she may be a Planet, tell us whether she may be one of the seven Planets, who are called Errones in Latine, (not for that they have an erroneous, but because they have a various motion) or whether she may be an eighth Planet, that so wee may make up our week of eight dayes; for why should not mother Earth have one day of the week, aswell as the other Planets, to carry her name? . . . Againe, if the Earth be a Planet, and each Planet hath its period of time for finishing its course: Saturne 30. yeares, Jupiter 12. Mars 2, &c. What is the time which you will allot to the Earth for the accomplishing of her annuall motion? If it be true, that the lower the Planet is, the swifter it is in its annuall motion; as the Moon in 27. dayes, and 8. houres, doth finish her course, which Saturne ends not but in 30. yeares space; doubtlesse, this Earth-planet, being the lowest of all, must in a very short time expire its annuall race. Moreover, if the Earth be the right Planet, Sol, who is the King of this planeticall Common-wealth, cannot have his throne in the midle, as Antiquity, and Truth too have placed him; for hee shall have three on his one hand, and four on the other, and so cannot impart his light equally to all.[569]
Ross’s ignorance of astronomy was no bar to his free use of invective and vituperation, but it did not assist him in producing any arguments except the sort that either clouded the issues or appealed to narrow prejudices. But Ross was the last voluble champion of bigoted Aristotelianism in an age that was moving rapidly away from the old scholastic philosophy. The very violence of his defense of the old ideas was symptomatic of the hopelessness of a losing cause. The new experimental science had taken firm root in England and had been making steady progress for a century. It was now rapidly gathering greater momentum and sweeping before it the last vestiges of really effective opposition.
In 1645 the particular group of scientists who were later to found the Royal Society began their meetings in London and Oxford. At this same period the influence of Descartes first made itself felt in England, and reinforced the tendencies, [283] already well established, toward the mathematical interpretation of the physical world and the idea of the infinity of the universe.[570] Thomas Hobbes’s provocative materialistic philosophy was promulgated and became a subject of controversy during the next decade. Henry More, the most famous of the Cambridge Platonists, accepted the discoveries of the new science and its fruitful assumption that a world created geometrically could be fully interpreted only through the aid of mathematics, and sought to combine them with a philosophy of volition and of the soul which should avoid both the dualism of Descartes and the mechanistic materialism of Hobbes. More, in 1642, had published a volume of four philosophical poems, entitled ψυχωδια Platonica: or A Platonicall Song of the Soul.[571] The second of these poems, “Psychathanasia,” contained a canto in praise of the Copernican theory, giving the arguments in its favor and refuting the attacks of its opponents.[572]
More’s work and influence, however, belong more truly to the succeeding age. In fact, in so far as it is ever possible to select a particular year as the boundary between two eras, the year 1645 may well be chosen as the beginning of a new period. Both in science and in philosophy, the men who were just then coming on the stage in England were the ones whose parts were to capture the imagination and dominate the thought of the succeeding decades. It is therefore fitting that this study of the progress of scientific and astronomical thought in England should end here, at the point from which most studies of the later period begin.
It is difficult to bring a study of this sort to a close, however, without at least a passing reference to Milton, for students of literature have long been inclined to accept the astronomical passages in Paradise Lost—particularly the first part of the eighth book, where Adam and the angel Raphael discuss the [284] rival systems of the universe—as a summary of the conflicting opinions as they appeared to Milton’s contemporaries in the middle of the seventeenth century. Such a notion is definitely misleading. In Milton’s day, as we have seen, the scientific rival of the Copernican system was the system of Tycho Brahe, not the ancient, unmodified Ptolemaic cosmology, with its nine or more geocentric spheres. Had it been Milton’s intention to make his poem exemplify current astronomical thought, he might easily have adopted the Tychonic cosmology as the basis for his epic, without materially altering the imaginative picture of the universe given in Paradise Lost. Therefore, those who support the view that Milton was deeply learned in the astronomical science of his day, and that, though at heart probably a Copernican, he retained the old astronomy in the framework of his epic merely because of its greater poetic value,[573] must face the question of why he made no mention whatever of the Tychonic plan of the universe.
On the other hand, the problem disappears and Milton’s use of astronomy becomes more rightly understood when we keep clearly in mind that the author of Paradise Lost was a poet, not a scientist, and thereby avoid the tendency of many of his admirers to make exaggerated claims concerning the extent of his astronomical learning. It is helpful, in this connection, to make a sharp distinction between mathematical or theoretical astronomy, and what we might term descriptive astronomy. When the cosmological passages in Milton’s poetry are carefully examined, they reveal no evidence that he had any profound knowledge of theoretical astronomy. He probably had never given much serious thought to the problems connected [285] with the true order and motions of the planets, and was not qualified to determine intelligently, from the mathematical and scientific point of view, the respective merits of the various systems. His poems show no signs of that intimate familiarity with practical astronomical observation and calculation that we find so consistently in Chaucer, and his scientific knowledge in such matters was probably inferior to Donne’s, and certainly to Gabriel Harvey’s.
On the other hand, no poet had a more extensive and intimate acquaintance with what may be called descriptive astronomy than Milton, or made finer use of it in his poetry. The configuration of the constellations and their positions on the celestial sphere were ever in his mind’s eye, and the revelations due to the telescope—no longer novelties in Milton’s day, it must be remembered—exercised a profound effect upon his imagination.[574]
The explanation of Milton’s distinctive use of astronomy is to be found in his sources.[575] The textbooks of astronomy which Milton recommended to his students, and with which he himself was undoubtedly most familiar, were Sacrobosco and Manilius.[576] In the list of authors he suggests in the tractate Of Education no modern writers find a place. Astronomy is represented in this group by Aratus, Manilius, and Lucretius,[577] [286] all of whom attracted Milton by their poetical descriptions of the heavens.
Having studied the heavens with these ancient manuals and poems as his guides and sources of inspiration, Milton’s imaginative picture of the universe was intimately interwoven with the Aristotelio-Ptolemaic conception of concentric spheres. The other great influence on his imagination, when it turned toward the stellar universe, was the telescope, and the new facts it had revealed concerning the heavenly bodies. Except for the passages discussing the Copernican system, there is nothing in Milton’s references to astronomy that might not have been derived from these two sources.
Milton, however, must have been well aware that the old Ptolemaic system had been almost completely abandoned by the scientists. His knowledge of Galileo’s Dialogo . . . sopra i due massimi sistemi del mondo Tolemaico e Copernicano (1632)[578] was sufficient to make him realize that fact, even had he been entirely ignorant of the trend of scientific thought in England. As a poet, accepting the Renaissance ideal of the epic as the embodiment of the highest learning of the age, he may well have felt it necessary to make some mention of the new philosophy which was gradually superseding the old. Whatever his reasons, Milton did not, as a preparation for this part of his task, embark upon a thorough and profound study of the basic mathematical principles of the various astronomical theories. Instead, as Professor Allan H. Gilbert has shown,[579] he turned principally to Galileo’s Dialogue of the Two Chief Systems of the World.
There was, certainly, no better single, nonmathematical source. Galileo, however, had opposed only the Ptolemaic system to the Copernican, since the former was the one still held, in his day, by his Aristotelian and theological adversaries [287] in Italy and was much more easily refuted than Tycho’s system. Milton’s reliance on Galileo’s Dialogue, then, is probably the reason why we find no mention, in his poem, of the Tychonic universe. But that need not surprise us, for Milton as a poet justified the use of the materials that he chose. We of today, therefore, should read the cosmological passages in Paradise Lost as great poetry, the product of the combined influence upon Milton’s imagination of the ancient astronomical poets and the recent telescopic discoveries. We should not be misled into thinking of them as important documents describing accurately the state of astronomical opinion in England in the mid-seventeenth century.
The preceding chapters have been devoted to analyzing the old system of cosmology and the changes it underwent as a result of the theories of Copernicus and his successors, and to tracing the course of astronomical thought in England up to the year 1645. In order to get a complete picture, the works on astronomy published in England during this period have been surveyed, with special emphasis upon the ideas and writings of the men recognized by their fellow countrymen as the most learned mathematical scientists. The constant aim in this study has been to assemble the material indispensable not only to the adequate explanation of the many references to cosmological matters in the literature of the period, but also to the fuller and more complete understanding of the current conceptions of the system of the universe and the gradual but significant changes which they underwent during these years.
The English scientists of the sixteenth and seventeenth centuries, on whose ideas and writings our conclusions have been based, were not unknown investigators working in isolation, far removed from the main stream of contemporary life and thought. On the contrary, they were, as we have seen, actively associated with a large circle of persons famous for the parts they played in the history and literature of the Elizabethan age.[580] Their books, furthermore, were widely read in England, often going through several editions.
The picture of astronomical thought in Renaissance England which we have gained from a study of these books has led us to a new conception of the scientific spirit of the age. No longer can we accept, for example, the notion that sixteenth-century English science was dominated by a narrow Aristotelianism. We have discovered that the philosophical background of the chief scientists was predominantly Platonic, and that they emphasized the Pythagorean element in Platonism which sought to interpret nature in mathematical or quantitative terms and thus provided the philosophical sanction for the new experimental method. The mystical attitude which saw God as the great geometer and looked upon the mathematical harmonies to be found in the material world as direct revelations of the Deity, also had its roots in Platonism, and was the source of inspiration for the religious glorification of the new discoveries of science as manifestations of the wonderful workmanship of the Creator. The ideas of certain pre-Socratic natural philosophers, particularly those of the early atomists regarding the infinity of worlds, were also brought forward repeatedly by the English scientists in opposition to the Aristotelian doctrines.
The entire tradition of science in England was, in fact, more against Aristotle than for him. Roger Bacon had been the chief dissenter from the rigidity of the Thomist synthesis of Aristotelian science and Christian theology, and had sought to use the newly discovered scientific works of the Greek and Arab philosophers as a foundation for future progress rather than as material for constructing a complete system of knowledge in which all scientific and theological questions should be given definite and final answers. This spirit, never lost by his successors, acquired a new vigor in the middle of the sixteenth century, when his English followers, in unbroken ranks, confidently advanced upon the narrow-minded supporters of Aristotle’s infallibility, placing their faith in the well-tried weapons of experimental observation and mathematical reasoning.
Closely connected with the freedom of English science from Aristotelian domination was its independent attitude toward all [290] accepted authorities. Many quotations have been given, in the preceding chapters, illustrating the insistence of English scientists that all theories, ancient or modern, must be verified by observation and experiment before being finally accepted.
This survey has also revealed important facts concerning the interest in the new science and the part played in its advancement by the learned scholars, on the one hand, and the unlearned practical workers, on the other. The group of English humanists at the beginning of the sixteenth century were distinguished for their sympathy with the new scientific movement. Some, like Linacre and Tunstall, took an active part in it, but all lent it their patronage in varying degrees. Sir Thomas More and his circle took the lead in advocating the writing of learned works in the vernacular, and later scientists, when they wrote in English, exhibited a style noteworthy for its clarity, directness, and vivid dramatic qualities—the very features that stand out in the writings of More and his school.
This vernacular tradition for scientific works and translations was the vital connecting link between the learned scientists and the general public. It was primarily instrumental in bringing into prominence a large and influential group of able practical workers in the sciences. The scholars, inspired by motives of patriotism and by a vision of the glorious possibilities of applied science for improving the lot of mankind, wrote and translated the books necessary to enable their less learned countrymen to acquire a firm grounding in the principles of the mathematical sciences and an acquaintance with all the essential knowledge then in existence relating to those subjects. The high state of practical mathematical learning and its wide diffusion in sixteenth-century England were commented upon by one of the leading historians of early English science nearly a century ago.[581] He quite rightly attributed these facts to the superior quality of the vernacular textbooks which the ablest English scholars of the time prepared in order that the “mechanicians” might have the means of combining sound [291] principles with their technical skill. The close understanding and co-operation between scholarly scientist and technician was an outstanding characteristic of the scientific movement in England from 1550 onwards. Co-operation among the leading scientists themselves was likewise a regular practice for over one hundred years before the foundation of the Royal Society.
Turning from observations concerning the general state of scientific learning and the progress of the movement as a whole to the special problem of the introduction of the new astronomy of Copernicus, we may briefly summarize the significant conclusions derived from our study of the astronomical treatises of the period. In the first place, the new heliocentric system was mentioned in nearly every important English textbook of astronomy from the time of Robert Recorde onward, with the comment that it would “save the phenomena” as fully as the older system. Although some scientific writers rejected it as a physical truth, none embarked upon any bitter attacks against it. The scientists whom contemporaries recognized as most eminent, however, were unanimous in adopting the Copernican theory mathematically, and most of them were among the open advocates of its physical truth, especially so far as the rotation of the earth was concerned. The failure to detect stellar parallax, it is true, caused some to reserve judgment on the question of the earth’s revolution about the sun until more definite proof was available—a justifiable attitude for the conservative scientist.
But not all of the English astronomical writers adopted this more cautious position regarding the new astronomical theories, although all insisted that Copernicus’ doctrine must be judged by the test of experimental observation. One of them, Thomas Digges, was the pioneer in decisively shattering the outer wall of the old cosmology and incorporating into the Copernican system the conception of an infinite universe, with the fixed stars, similar in nature to our sun, scattered at varying distances throughout endless space. Other Englishmen, notably Gilbert and those who followed him, took the lead in suggesting [292] physical causes for the motions which Copernicus assigned to the earth. English astronomers were already making telescopic observations of the heavens before Galileo’s discoveries were announced, and showed special eagerness in confirming them and suggesting their possible relation to the problems of physical astronomy.
Among scientists of recognized standing in England, the old Ptolemaic system was completely discredited from the end of the first decade of the seventeenth century onward. The geocentric system proposed by Tycho Brahe, still defensible from the scientific point of view, and not the unmodified Ptolemaic system, was the one expounded by the period’s important astronomical textbooks which did not support the Copernican system in its entirety. English Tychonians, however, were inclined to modify the Danish astronomer’s hypothesis to include the earth’s diurnal rotation due to magnetic force, thus achieving a system not inconsistent with the new telescopic discoveries or the conception of the infinity of the stellar universe. As we approach the middle of the seventeenth century, the system of Tycho, or this modification of it, was the scientific rival of the Copernican plan, and we must be on the alert not to take references to the Tychonic system as allusions to the ancient Aristotelio-Ptolemaic cosmology.
The English books dealing with astronomy thus reveal the steady progress of the new astronomical ideas—a progress whose every step was closely bound up with that gradual increase in astronomical knowledge which was disproving the old doctrines and providing scientific data to lend greater credit to the newer theories. These books likewise disclose the rapidity with which English prose, in the mid-sixteenth century, achieved a remarkable maturity and precision in the clear exposition of complex scientific subjects. A comparison of the passages quoted from Caxton’s Mirrour of the World and Robert Copland’s translation of the Kalendrier des bergiers[582] with the prose of Recorde, Digges, or Hood will bring [293] home to the reader the tremendous advance made within a few decades.[583]
Part of this progress in the skill with which English was made to serve the exacting literary requirements of scientific exposition was due to the superior knowledge of their subject possessed by the later authors. Much, however, was the result of the well-defined, carefully formulated purpose of the English writers. The leading scientists had a patriotic feeling for their native tongue and a confidence in its ability to meet fully the often difficult demands of expressing, briefly and clearly, abstruse technical or philosophical ideas. This attitude has been illustrated in many of the quotations we have given from their works. Since their prose was designedly utilitarian and the audience they aimed at was not primarily one composed of scholars but rather of intelligent artisans, the writers on science naturally followed the rules which Sprat tells us the early members of the Royal Society imposed upon themselves, and preferred “the language of Artizans, Countrymen, and Merchants, before that, of Wits, or Scholars.”[584] Their ideal, likewise, was the same: “a close, naked, natural way of speaking; positive expressions; clear senses; a native easiness: bringing all things as near the mathematical plainness, as they can.” Passing fads of literary style, like euphuism, had little effect upon the main current of scientific prose. These scientific writers were not infected with that overeager desire to “augment” the language, which was productive of so much tautological phraseology and so many “ink-horn terms.” They used their native tongue with confidence and pride, despite [294] their occasional insertion of the conventional apologies for writing in the vernacular.[585]
Yet there was a certain type of augmentation which the scientists were well aware that the English language definitely needed—namely, a precise vocabulary of scientific terms. When English lacked an equivalent for a word in a Greek or Latin technical treatise, the writers seeking to make ancient scientific knowledge available in the vernacular had to supply this deficiency. Their problem was whether to coin a new word from English roots, or to adopt and seek to naturalize the Latin or Greek term, at the same time giving it a precise definition. At the beginning, the English authors wavered between the two courses. Recorde, for example, in his Pathway to knowledg, usually introduces in his geometrical definitions both the classical term and an English equivalent which he has invented. He speaks of “parallel or gemowe lines,” but for “parallelogram” he coins the hybrid term “likejamme.”[586] In his text he may, for some terms, consistently employ his new-minted English word; for others, he generally reverts to the Latin or Greek word.
Later writers realized that it was as easy to naturalize a Latin term as to introduce a strange new word formed from roots that were native to the English tongue—or were so considered by the Elizabethans. In the former policy they saw certain advantages, and they were aware that there were classical precedents for linguistic borrowing. Consequently, they decided to take over boldly the Greek and Latin terminology wherever no obvious and familiar English equivalent existed—a decision which had a most important influence on the later [295] development of the English language. The reasons which prompted this action are nowhere more clearly stated than in Thomas Digges’s preface to the short treatise on solid geometry which he added to his father’s Pantometria when he completed and published that work in 1571:
. . . let no man muse that writing in the English toung, I haue retained the Latin or Greeke names of sundry lines and figures, as cordes Pentagonall, lines Diagonall, Icosaedron, Dodecaedron or such like, for as the Romanes and other Latin writers, notwithstandinge the copiouse and abundant eloquence of their tongue, haue not shamed to borrow of the Grecians these and many other termes of arte: so surely do I thinke it no reproche, either to the English tongue, or any English writer, where fit words faile to borowe of them both, but rather should we seeme thereby to do them great iniurie, these beeing in deede certaine testimonies and memorials where such sciences first tooke their originall, and in what languages and countries they chieflie florished, which names or wordes how straunge soeuer they seeme at the firste acquaintaunce, by vse wyll growe as familiar as these, a Triangle, a circle, or such like, which by custome and continuance seeme meere English, yet to auoide all obscuritie that maie growe by the noueltie of them, I haue adioined euery of their diffinitions. . .[587]
These English scientists were the heirs of a continuous tradition of excellent prose writing in the vernacular, which had been preserved, without a break, in the devotional literature and had made possible the fully developed prose style of Sir Thomas More and his school. They were therefore able to write with ease and assurance a prose that was not only clear, direct, and flexible in its style, forsaking all attempts at mere ornamentation, but was also ready to use dramatic touches and the devices of the pulpit and of the stage to arouse and hold the interest of the reader. For that reason it usually makes much better reading than the bare, factual type of prose, without in any way sacrificing the qualities necessary to clear exposition.[588]
One other significant fact concerning the scientific spirit in Renaissance England—a fact we have seen repeatedly brought into prominence in the course of our study of astronomical thought—deserves special emphasis in our conclusion. This is the revelation that most of the fruitful ideals of science that are popularly associated with the work of Francis Bacon and the seventeenth century were already part of the publicly avowed creed of the English scientific workers throughout the latter half of the sixteenth century. The spirit of revolt against ancient authority, and the fair-minded, yet independent, criticism of all ancient doctrines; the conviction that the experimental method was the only sure road for arriving at scientific truth; the glorification of the utilitarian value of science for the relief of man’s estate; the recognition that even the humblest worker could render genuine service in the great co-operative task of scientific research; and, finally, the enthusiastic belief in future progress through the advancement of science—from all these elements was the scientific faith of the Elizabethan openly compounded.
Nor were the Englishmen who were Bacon’s predecessors at all backward in their professions of this faith. We have found their scientific spirit, in its various phases, eloquently expressed in the writings of Recorde, Dee, Digges, Norman, Borough, Blagrave, Gilbert, Wright, and many other Elizabethans. Yet this attitude toward science was not the peculiar possession of Englishmen in this age. In a translation of a French work we find perhaps the finest and most extensive expression of the theory of progress, and the ardent belief that, by augmenting through scientific investigation the learning received from the ancients, human effort could achieve an almost limitless increase in knowledge and power. Louis Le Roy, professor of Greek at the Collège Royal in Paris, published in 1575 a lengthy work discussing the state of human learning in all ages, entitled [297] De la Vicissitude, ou variété des chases en l’univers.[589] It was translated into English in 1594 by Robert Ashley, a lawyer then residing at the Middle Temple, because of the “great liking” which he “saw generally conceived of the worke,” and was dedicated by him to Sir John Puckering, Lord Keeper of the Great Seal. The book was printed by Charles Yetsweirt, a Clerk of the Signet, and the holder of the royal patent for the printing of law books, with the title, Of the Interchangeable Course, or Variety of Things in the Whole World.[590] It was undoubtedly known to Bacon, although, as was often his custom, he made no specific acknowledgment of his indebtedness.
Ashley’s English version is an outstanding example of eloquent and moving English prose, and has a rhythm which makes it often resemble very closely the style of Sir Thomas Browne. The last book of the volume is entitled, “Whether it be true, or no, that there can be nothing said, which hath not bin said before; And that we must by our owne Inuentions, augment the Doctrine of the Auncients . . .” This book elaborates the thesis that ancient learning is a heritage which should form the foundation for further progress. Every man should contribute to its augmentation, and, if the people of the present day would apply themselves diligently to this task, some of them might equal the achievements of the greatest names among the earlier scientists:
[298]And let vs not be so simple, as to attribute so much vnto the Auncients, that wee beleeue that they haue knowen all, and said all; without leauing anything to be said, by those that should come after them. They haue not bin so arrogant, as to looke that none should meddle, or deale with those matters which they had handeled: But on the contrarie, considering the difficultie of knowledge, and the weaknes of mans vnderstanding, they haue exhorted others to trauaile therein; speaking rather to stir them vp, and prouoke them thereunto, then to keepe them back, or stay them from writing. Let vs not thinke that nature hath giuen them all her good gifts, that she might be barren in time to come: but that as she hath in times past brought foorth certaine notable personages, who haue manifested many of her secrets; so she can againe bring foorth, such as by the influence of heauen, and a singular inclination, by liuelynes of vnderstanding, and perseuerance of labour, shall attaine thither; whither long experience, diligent obseruation, and subtilitie of reason, haue not pierced till this present. She is the same that she was in the former famous ages: The world is such as it was before: The heauen and the time keepe the same order which they did; The Sunne, and thother Planets, haue not changed their courses; and there is no starre remoued out of his place: The Elements haue the same power; men are made of the same matter, & in the same sort disposed as they were in old time. And were not the maner of lyuing corrupted, which we vse, preferring idlenesse before diligence, pleasure before profit, and riches before vertue; nothing would let, but this age might bring foorth as eminent personages in Philosophie as were Plato, and Aristotle; in Physick as Hippocrates, and Galen; or in the Mathematicks as Euclide, Archimedes, and Ptolomey. Considering the help which we receiue of their books, the examples wherwith antiquitie hath instructed vs, so many obseruations, and inuentions sithence their time, and so long experience of all things: In such sort, that (if we consider it well) there was neuer age more happie for the aduancement of learning, then this present; if weying the shortnes of mans life, we resolue to employ our whole endeauour & industrie, on the studie of true knowlege. Wisdom hath not fulfilled her work; much remaineth, and will alwaies remaine: and there will neuer be wanting occasion to add therunto. Trueth doth offer her selfe to all those that wil seek her, and are of capacitie to receiue her: albeit Democritus complayneth, that she is hid in a place as deep as a well, wherhence (in his opinion) it is not possible to draw her foorth. Whosoeuer giueth himself to it in good earnest, shall find alway somewhat to do therin. All the mysteries of God and secrets of nature, are not discouered at one time. The greatest things are difficult, and long in comming. How many are there, not as yet reduced into art? How many haue bin first knowen and found out in this age? I say, [299] new lands, new seas, new formes of men, maners, lawes, and customes; new diseases, and new remedies; new waies of the Heauen, and of the Ocean, neuer before found out; and new starres seen? yea, and how many remaine to be knowen by our posteritie? That which is now hidden, with time will come to light; and our successours will wonder that wee were ignorant of them.[591]
Here the ideas, and some of the words, correspond to those later used by Francis Bacon. Certainly, therefore, we must look to the sixteenth century, not the seventeenth, for the genesis and the first clear formulation of those ideas that have ever since been intimately associated with the development of modern science. Once our glance passes beyond the dominating figure of Bacon, we discover that the picture he drew of the attitude toward science in his day was too frequently a distorted image created for purposes of propaganda. After becoming acquainted with the works of his predecessors, we cannot do less than pay a belated tribute to the scientific spirit of the Elizabethans.
In compiling the following list, the most difficult problem has been to arrive at some reasonably consistent method of determining what titles to include. The scientific books which deal wholly, or principally, with astronomy have presented no difficulty, and I believe that my list will prove complete as far as these works are concerned. But there are a great number of other books, such as those on navigation, for example, in which the astronomical material is subsidiary, yet fairly extensive. In these cases my rule has been to list only those in which I found sections on astronomy that were sufficiently detailed and important to warrant their inclusion. Literary and philosophical works whose references to cosmological questions are merely incidental have generally been omitted. Occasional exceptions, however, have been made to this rule; for instance, two of Bacon’s works, and Ralegh’s History of the World, have been given a place because they contained some of the longest, best-known, and in some ways most influential of the incidental discussions of this type.
No attempt has been made to list all the theological works which, in expounding the biblical account of the world’s creation, referred, in passing, to other cosmological theories. Works on astrology, too, have consistently been excluded unless they also contained expositions of the more reputable sister science of astronomy, upon which the astrologians based their predictions.
An asterisk preceding an entry indicates that the book has been discussed in the text. To the other entries, I have usually added a brief note to suggest the nature and importance of the book. For purposes of cross reference, I have frequently inserted under the later editions of a book the date of its first edition.
The titles of the books have been recorded as they appear in the first edition; in listing the later editions, the orthography of the first edition has usually been followed. No bibliographical descriptions other than author and title have been given. Instead, the Short-Title Catalogue number has been inserted in square brackets after each entry.
Following the practice of the Short-Title Catalogue, I have included books printed in English on the Continent, but not the editions of Latin works by English authors which were printed abroad. There were only two such works of genuine importance which did not also see an edition printed in England. These were George Buchanan’s De [302] Sphaera and Nicholas Hill’s Philosophia Epicurea, and I have felt justified in departing from strict consistency by giving them a place in my list.
The following books and articles represent a selected list of secondary and bibliographical works. A few important editions of the writings of the chief Renaissance astronomers and scientists have been included because they contain valuable introductions and notes. The list has been strictly limited to the works which seemed at once the most reliable and the most readily usable; and highly specialized studies of sixteenth- and seventeenth-century continental scientists have therefore been omitted. The titles of original sources have not been repeated here, but may be located in the text by consulting the index.
Ptolemy’s Almagest: First edition of an epitome (Peurbach and Regiomontanus), Venice, 1496; first complete edition, a Latin translation from the Arabic, Venice, 1515; first Latin translation from the Greek, by George of Trebizond, Venice, 1528; first edition of Greek text, by Simon Grynaeus, Basel, 1538.
Aristotle’s works: First complete edition, with Greek text, by Aldus Manutius, Venice, 1495-98; a vast number of editions of Latin translations had been published much earlier.
Plato: Ficino’s Latin translation of the works, Venice, 1482; first Greek edition, Venice, 1513.
Alfraganus: Latin translation, Ferrara, 1493; other editions, Nürnberg, 1537, and Paris, 1546.
Albategnius: First printed with Alfraganus, in Nürnberg edition, 1537.
Alpetragius: His Planetarum theorica was first printed, from a Latin translation of a Hebrew version, in an edition of Sacrobosco’s Sphaera mundi published at Venice in 1531.
Proclus: Latin translation of his Sphaera by Thomas Linacre first printed at Venice in 1499; there were numerous subsequent editions.
Simplicius: Commentary on Aristotle’s De Caelo, Venice, 1528.
Diogenes Laertius: The first Latin edition of his “Lives, Doctrines, and Maxims of Famous Philosophers” was published in Rome before 1475; another edition was printed in Venice in 1475 and a total of sixteen editions had appeared by 1500; the first Greek edition was published at Basel in 1533.
Cleomedes: First Latin edition, Venice, 1488; first Greek edition, Paris, 1539.
Plutarch: A Latin translation of the Lives was published in Rome about 1470, and there were numerous subsequent editions in Latin; the first Greek edition was printed at Florence in 1517.
Lucretius: First edition, Brescia, ca. 1473.
Pliny: First edition, Venice, 1469; there were many subsequent editions.
Macrobius: First edition, Venice, 1472.
Martianus Capella: First edition, Venice, 1499.
Chalcidius: First edition of his commentary on the Timaeus, Paris, 1520.
The facts concerning the early editions of these works have been taken mainly from Sarton’s Introduction to the History of Science, supplemented in certain instances by Hain’s Repertorium Bibliographicum.
A second edition, likewise in folio, was printed at Basel in 1566.
A third edition, printed at Amsterdam, in quarto, in 1617, was entitled: N. Copernici . . . Astronomia instaurata, libris sex comprehensa, qui de Revolutionibus Orbium Coelestium inscribuntur.
I have used a copy of the second edition kindly lent me by Dr. Edwin Hubble, of the Mount Wilson Observatory.
“The different explanations which have been given of the connexions of the heavenly bodies with each other, forming what are called systems of astronomy, are the consequences of long trains of reasoning upon what has been observed on earth and in the heavens, upon the changes of apparent place which may be imitated on the globes which this book is intended to describe. With these astronomical systems we have nothing to do: as far as power of using and understanding the globes is concerned, it matters nothing whether their owner imagines the sun to move round the earth or the earth round the sun. The globe enables us to imitate the appearances of the heavens; two persons, one of whom explains these appearances rightly, and the other wrongly, both go to the globe for the same purpose, use it in the same manner, draw the same conclusion from it, and speak of that conclusion in the same words. It is then totally unnecessary, in teaching the use of the globes, to enter upon the reasons why the appearances are what they are . . .
“There is another and a still stronger reason why a book on the use of the globes should contain nothing but apparent astronomy. The time was, when every educated person was tolerably well acquainted with the appearances of the heavens, and came to the discussion upon Ptolemaic and Copernican explanations with a clear idea of what it was about. It is not so now: few persons look at the heavens, while most learn a certain astronomy from books. The books teach the true or real motions of the heavenly bodies, those in particular of the solar system, so well, that if their reader could take up his residence in the sun, he would find himself quite at home and would have daily illustrations of the Copernican theory passing before his eyes. But, confined to this earth, he does not see written in the heavens the astronomy he learns: no wonder, then, that he does not care to look at the heavens, or feel much interest in the globe, which is only an imitation of the apparent motions.”
[Page numbers in italic type refer to the chronological list of astronomical books in Appendix A.]
[The end of Astronomical Thought in Renaissance England by Francis R. Johnson]